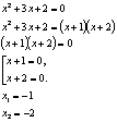Кейбір алгебралық
есептердің геометриялық интерпретациясы
Қарабаев
А.С., математика пәнінің мұғалімі
Дарынды
балаларға арналған «Дарын» мектеп-интернаты
Андатпа. Бұл мақалада
абстракты ұғымдар мен кейбір алгебралык есептерді сандық
модельдеу жолымен геометриялық интерпретация арқылы шығару тәсілі
қарастырылып, зерттелген. Қазіргі
кезеңде математикалық модельдеу практикалық, қолданбалы
ғылым саласында маңызды роль аткаратындығы белгілі. Автор осы
жұмыста сандық модельдердің «бірлік шаршылар мен бірлік текшелер»
жиыны болып табылатын түрлерін ұсынған. Солар арқылы
кейбір алгебралық есептерге геометриялық мазмұн, мағына
беріп, геометриядағы «аудан, көлем» ұғымдары
арқылы екінші, үшінші дәрежелік
теңдеулерді шешуде, сан тізбегі мүшелерінің қосындысын
табуда өзіндік ерекшеліктері бар тәсіл ұсына білген. Бұл тәсілдің ондық
санақ жүйесіндегі санның позициялық
құрылымымен үндестікте берілуі назар аударуға
тұрарлық.
Abstract . On given work some abstract conceptions and some
algebraic sums are looked over and researched by geometric interpretation and
numerical modeling. Nowadays it is known that mathematical modeling plays great
role in practices and usage science. Author offers "square and cubic
metres" of numerical modeling. With the help of this geometric content is
given to some algebraic sums, and the nations such as "area", and
"capacity" are used to summarize second and third degreed equation,
and to sum up terms of progression. Numeric positional struction of demical
numeration is worthy to pay attention.
Ғылым мен техниканың, кұрылыстың даму барысында, физикалық модельдеуден гөрі математикалық модельдеудің маңызы ерекше екендігі белгілі. Ол ғылым мен техниканы, құрылысты дамытуға кететін каражатты мейлінше үнемдеуге және де қарастырып отырған объектіні басқа беймәлім қырлары бойынша тануға мол мүмкіндік береді.
Бұл мақалада кейбір
алгебралық есептердің бізге беймәлім қырларын
ашуға мүмкіндік беретін математикалық модельдеудің бір
түрі ретінде "бірлік шаршылар, бірлік текшелер жиыны" деп
аталатын сандық модельдерді ұсынып отырмын.
Бастауыш сыныптарда санды оқыту
мен санауға үйретуде бұрыннан колданылып келген сандық
модельдер (таяқшалар, дөңгелекшелер және т.б.)
ондық санак жүйесіндегі санның позициялық
қүрылымын өрнектеуге қолайсыз болғандығы
белгілі; заттар мен сандар жиыны арасындағы өзара - бір мәнді
сәйкестікті анықтаудың алғашқы қадамдарында
оқушылар үнемі қателесетін "Пиаже эффектісін"
жоюға қауқарсыз еді.
Ал, жоғарғы сыныптарда
екінші, үшінші дәрежелі көпмүшеліктердің,
теңдеулердің түбірлерін табу тәсілдерінің
сан-алуан екендігін білеміз. Көпмүшеліктерді, теңдеулерді
позициялық құрылымға сәйкес сандық
модельдеу, осы тәсілдердің қатарын жаңа бір,
өзіндік артықшылығы бар әдіспен толықтыруға
мүмкіндік береді. Кейбір алгебралық есептердің
геометриялық интерпретациясы (түсіндірілуі), ол есептердің
жаңа мағынасын ашуға, ол мағыналардың
геометриялық ұғымдармен (мысалы, аудан, көлем ұғымдары)
байланысты шешуге мүмкіндік береді. Алгебралык есептердің
өмірлік құбылыстармен байланысы күшейтіледі.
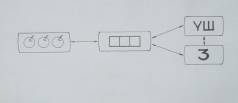
Санауды үйренуден бүрын, санның атауын білген дұрыс. Сондықтан да санауға оқыту, балалардың есте сақтауы мен сандардың атын дұрыс қайталауды оқып-үйренуінен басталады. Бұл әсте де оңай емес. Көбінесе балалар онға дейін санау барысында: «бір, екі, үш, бес, сегіз...» деп бірнеше сандардан секіріп кетіп отырады. Бұған таң қалуға да болмайды, өйткені санау - ол заттардың қандайда бір жиынының элементтері мен сан атаулары қатары арасында өзара - бір мәнді сәйкестікті тағайындау болып табылады, сонымен қатар ол жиын шамасы санау кезінде аталатын сан есіммен ең соңында белгіленетіндігін түсіну. Мұнда «сан» ұғымын өзара бір мәнді сәйкестік орнатылған жиындар класының қасиеті ретінде түсіну керек.
|
1- сурет. |
Балаларға абстракты сандар жиыны
мен нақты заттар жиыны арасындағы өзара бір мәнді
сәйкестікті түсінудегі бұл еңбекті көп
қажет ететін (көп еңбектеңуді керек ететін) этапты
өтуге (игеруге) көмектесу үшін аралық көмекші
құрал енгіземін: квадрат (шаршы), тақталар (плиткалар) жиыны
- тек бір ғана қасиеті бар - ол оның мөлшері. Бұл
шаршылар балаларға санауды оқытуда - бірінші маңызды
қадамды жасауға - заттар, шаршылар, сан есім және цифрлар
арасындағы өзара алмасуды түсінуге көмектеседі.(
1-сурет)
|
а) б) 2 -
сурет. |
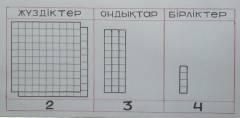
Шаршылардың басқа
сандық модельдерден (дөңгелекшелер, таяқшалар, т.б.)
ерекшелігі кемінде екі
артықшылығы болуында:
1.оларды дайындау оңай (мысалы картон немесе қатты қағаздан);
2.оларды бір жолаққа
біріктіру арқылы бірліктерді, ондықтарды, жүздіктерді жобалау
қолайлы;
Шаршылардың осы
артықшылықтары ондық санақ жүйесінде санның
позициялық (орналасқан жері) құрылымын өрнектеуге
анағұрлым дәл келеді (2-сурет, а).
Сонымен қатар шаршылар көмегімен ондық
бөлшектер мен жай бөлшектерді де оңай
оқып-үйренуге болады. (2-сурет, б).
Екінші дәрежелі
теңдеулерді шаршылар көмегімен шешуді қарастырайық. Ол
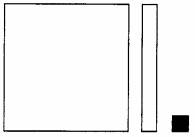
үшін алдын-ала төмендегі белгілеулерді енгізіп аламыз ( 3-сурет):
|
х2 х бос мүше 3-сурет |
1. үлкен шаршы (жүздік шаршы) « х2»
-екінші дәрежелі
көпмүшеліктің бірінші мүшесі;
2. жолақ бағана (ондык)
« х » - екінші дәрежелі көпмүшеліктің екінші
мүшесі;
3.«бірлік шаршы»- екінші дәрежелі
көпмүшеліктің бос мүшесін бейнелейді
Сонда екінші дәрежелі
теңдеулерді шешу есебі теңдеу қүрамындағы
көпмүшелікке сәйкес алынған құрама
бөліктерден «тік төртбұрыш құрастыру» есебіне
алмастырылады.[1]
Енді осы әдістемелік тәсілді
х2+3х+2=0 келтірілген теңдеуін шешу мысалында
түсіндірейік. Құрама бөліктерден тік
төртбұрыш құрастырамыз:
|
4-сурет |
Келесі мысал ретінде 2х2+5х+3=0
толық квадрат теңдеуін шешіп көрейік. Теңдеу
құрамындағы көпмүшелікке сәйкес құрама
бөліктерден тік төртбұрыш құрастырамыз (5-сурет).
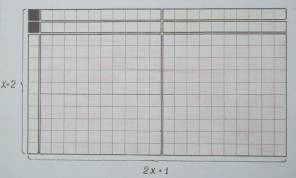
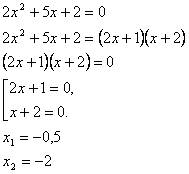
5-сурет
Егер құрама
бөліктерден тік төртбұрыш құрастыру мүмкін
болмаса, онда берілген квадрат
теңдеудің шешімі болмайды. Көз жеткізгілеріңіз келсе: х2+3х+3=0
теңдеуін шешіп көріңіздер.
Ал үшінші дәрежелі
теңдеулерді шешуге жоғарыда көрсетілген фигураларды
пайдаланар болсақ, алдын-ала өзгерістер енгізіп, белгілеп алуымыз
қажет:
1. Жоғарыда көрсетілген
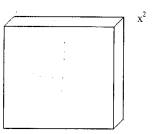
фигураларды кеңістіктік фигураларға дейін толықтырамыз (6-сурет);
Бірлік куб
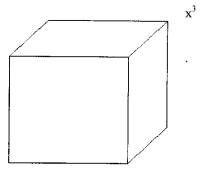
![]()
![]()
а
б в г
6 сурет.
Кеңістік фигуралары
«х3» - үшінші дәрежелі
көпмүшеліктің бірінші мүшесі бейнелейді
«х2» - үшінші
дәрежелі көпмүшеліктің екінші мүшесін бейнелейді.
«х» - үшінші дәрежелі
көпмүшеліктің үшінші мүшесін бейнелейді.
«бірлік куб» — үшінші
дәрежелі көпмүшеліктің бос мүшесін бейнелейді.
Енді бұл әдісті х3+6х2+11х+6=0
келтірілген үшінші дәрежелі теңдеуді шешу мысалында
қарастырамыз ( 7- сурет):


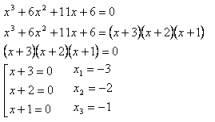
7-сурет
Және де 2х3 +7х2+7х+2=0 толық квадрат
теңдеуін шешуге қолданамыз (8-сурет).
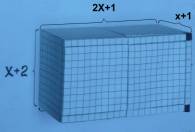
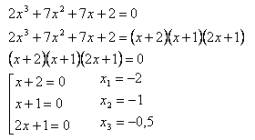
8-сурет
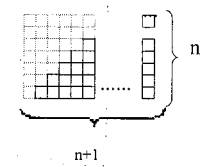
1+2+3+4+5+... + n қосындысын табу керек болсын.
Ол үшін бірлік шаршылардан
тұратын бағандарды пайдаланамыз. Яғни «1» санын – «![]() » бірлік шаршымен, «2» санын
» бірлік шаршымен, «2» санын ![]() екі бірлік шаршыдан тұратын бағанмен, «3» санын -
екі бірлік шаршыдан тұратын бағанмен, «3» санын - ![]() үш бірлік шаршыдан тұратын бағанмен, т.с.с
алмастырамыз[2.3]
үш бірлік шаршыдан тұратын бағанмен, т.с.с
алмастырамыз[2.3]
Сонда
n-
шаршы
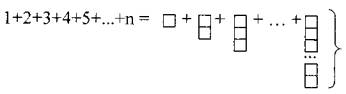
Бұдан келесі бірлік шаршылардан тұратын төмендегі фигура келіп шығады:
|
|
Енді берілген қосындыны табу үшін алынған
фигураны тік төртбұрышқа толықтырамыз. Сонда оның ені-n, ұзындығы
- n+1, яғни ауданы n(n+1)-ге
тең болады.
Сонымен ![]() біздің іздеп
отырған қосындымыз болады.
біздің іздеп
отырған қосындымыз болады.
Яғни ![]()
Шаршы тақтайшалардың келесі бір қолданылымы: 9-сыныпта тізбектер тақырыбын өткенде натурал сандардың, тақ натурал сандардың, жұп натурал сандардың алғашқы n мүшелерінің косындысын анықтайтын формулаларды алудың математикалық индукция әдісінен басқа жолын көрсету; қосындының мағынасын мөлшер (шама) теориясы бойынша аудан ұғымымен байланыстыру.
Бұл байланыс ![]() ; 1+3+5+7+...+(2n-1)=n2; 2+4+6+8+… +2n=n(n+1) қосындыларын (9-сурет, а б) табу барысында
айшықты бейнеленген.
; 1+3+5+7+...+(2n-1)=n2; 2+4+6+8+… +2n=n(n+1) қосындыларын (9-сурет, а б) табу барысында
айшықты бейнеленген.
Сол сияқты ![]() қосындысын есептеу формуласын,
қосынды мағынасын аудан-көлем ұғымдарымен
байланыстыру арқылы бірлік текше көмегімен модельдеу жолын
қолданып, шығарып алуға (9-сурет,в) болатынын
көресіздер
қосындысын есептеу формуласын,
қосынды мағынасын аудан-көлем ұғымдарымен
байланыстыру арқылы бірлік текше көмегімен модельдеу жолын
қолданып, шығарып алуға (9-сурет,в) болатынын
көресіздер


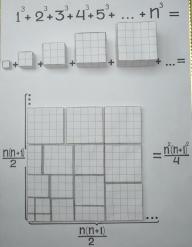
а б в
9 сурет
Мен, өзім ұсынып
отырған сандық модельдің бастауыш сынып оқушылары үшін санды
оқыту мен санауды үйрету барысында көп қателесетін
"Пиаже эффектісін" жоюға, сандарға амалдар қолдануда, көмекші
құрал болатынына сенемін. Мақалада кейбір алгебралық
есептерді геометриялық интерпретациялау
арқылы оларға жаңа мазмұн, жаңа мағына
беруге болатынын көрсеттім. Модельдеу әдісінің
артықшылығын, қарастырып отырған объектіге қатысты
зерттеу тәсілдерін өзара гармониялық үйлесім мен
тығыз сабақтастыра қолданғанда ғана күткен
нәтижеге жетуге болатынын, көрсетуге тырыстым.
Бұл жұмыстың идеясы мен нәтижесі орта
мектеп мұғалімдері үшін маңызды және
практикалық іс-әрекеттерінде кең қолданысқы ие
болады.
Қолданылған
әдебиеттер:
1.
Шыныбеков А.Н. Алгебра. Жалпы білім беретін мектептің 9 сыныбына
арналған оқулық. Алматы «Атамұра», 2005, 2013
2.
Валенкин Я.Н. Алгебра 9 класс для углубленного изучения математики
3.
К.Гинбаяси, президент АМІ, профессор; Н,Ямазаки, член АМІ, профессор
«Радостные уроки или Почему японские дети любят математику»