Подгорная В.В.

УО ФПБ «Международный университет «МИТСО»», Беларусь

Методы и приемы самостоятельной работы при изучении темы «Определенный интеграл»

Самостоятельная работа – это средство активизации учебной деятельности студентов. Вся самостоятельная работа, если она организована в качестве эффективного вида учебной деятельности, выполняется при участии преподавателя, который должен сформулировать цели и задачи самостоятельной работы, оказать необходимую консультативную помощь и осуществить контроль выполняемой работы.

Самостоятельная работа может быть индивидуальной, групповой или фронтальной, выбор формы зависит от цели и задач изучаемого материала. Кроме того, выбирая вид самостоятельной работы, необходимо учитывать уровень подготовки обучаемых и степень их мотивированности. Однако самостоятельную работу можно классифицировать не только по форме ее организации, но и по другим признакам. Это может быть воспроизводящая, эвристическая, реконструктивная либо исследовательская работа, выбор вида зависит от характера учебной деятельности, а если говорить о целевой направленности работы, то она может быть теоретической или практической, можно также выделить обязательную, альтернативную, общую и вариативную формы.

Сочетание тех или иных видов самостоятельной работы зависит от поставленных целей, например, усвоение основных теорем и понятий, анализ и сравнение изучаемых фактов. Выбор вида самостоятельной работы непосредственно завит от содержания учебного материала и этапа обучения студентов.

Рассмотрим основные виды самостоятельных работ:

1. Воспроизведение работы, или работа по образцу. Такой вид работы включает в себя задачу воспроизведения полученных знаний и умений. Все данные для нахождения искомого, а также способ выполнения задания предоставлены в самом задании или соответствующем алгоритме (образце) решения, можно предложить демонстрационные примеры с подробными инструкциями их решения. Такие действия способствуют наполнению студентами опорных фактов и способов деятельности, закреплению знаний, умений и навыков. В этом случае познавательная деятельность состоит в узнавании информации или действий с теми или иными объектами знаний. К таким заданиям можно отнести тренировочные упражнения по образцу.

Вычислить интеграл .

Данный интеграл не является табличным, т. к. аргумент функции не совпадает с переменной, стоящей под знаком дифференциала (x). Следовательно, подстановка приведет данный интеграл к табличному. Не следует забывать, что, вводя новую переменную t необходимо ввести не только ее дифференциал dt, но и новые пределы интегрирования. Если нижний передел переменной x был равен 0, то нижний предел новой переменной t будет равен , верхний предел переменной x был равен , тогда верхний предел новой переменной t будет равен .

.

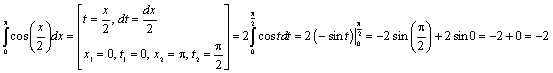Возвращаться к исходной переменной в этом случае не нужно.

2. Реконструктивная самостоятельная работа. Ее признаком является то, что уже в самом задании заложена общая идея решения, а студенту необходимо развить ее в конкретный способ или способы применительно к условиям задачи. Главное в этом случае – актуализация усвоенных знаний, умение выбрать и привлечь необходимые знания для решения задач. Здесь для познавательной деятельности обучаемых характерно обобщение полученных знаний.

Задачи для самостоятельного решения к главе 18

Уровень1

1. Вычислить интеграл ;

2. Вычислить интеграл ;

3. Вычислить интеграл ;

4. Вычислить интеграл ;

5. Вычислить интеграл ;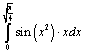

6. Вычислить интеграл ;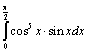

7. Вычислить интеграл ;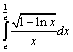

8. Вычислить интеграл ;

9. Вычислить интеграл ;

10. Вычислить интеграл ;

11. Вычислить интеграл ;

12. Вычислить интеграл ;

13. Вычислить интеграл ;

14. Вычислить интеграл ;

15. Вычислить интеграл ;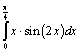

16. Вычислить интеграл ;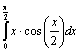

17. Вычислить интеграл ;

18. Вычислить интеграл ;

19. Вычислить интеграл ;

20. Вычислить интеграл .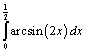

Уровень2

1. Вычислить интеграл ;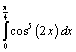

2. Вычислить интеграл ;

3. Вычислить интеграл ;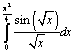

4. Вычислить интеграл ;

5. Вычислить интеграл ;

6. Вычислить интеграл ;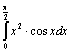

7. Вычислить интеграл ;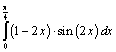

8. Вычислить интеграл ;

9. Вычислить интеграл ;

10. Вычислить интеграл .

3. Эвристическая самостоятельная работа. В данную разновидность необходимо включать нетиповые задачи, которые предлагают студентам нестандартные ситуации. В основе выполнения такой работы лежат поиск, догадка и реализация идеи ее решения. К таковым можно отнести рефераты, доклады с решениями задачи и некоторые задания по выбору.

4. Исследовательская, или творческая работа. При выполнении такой работы у студентов проявляется наиболее высокий уровень познавательности и самостоятельности. Выполняя творческую работу, студент глубоко проникает в сущность изучаемого явления, находит новые идеи в решении поставленных проблем. Творческая задача, если она решена, в итоге имеет объективную ценность.

Чтобы самостоятельная работа давала высокие результаты, она должна быть четко организована и правильно спланирована, кроме того, ее выполнение необходимо проконтролировать.

В процессе планирования собственной деятельности каждый преподаватель должен также планировать самостоятельную работу студентов – ее содержание, виды и формы, методы учета результатов, причем данная информация обязательно должна быть доведена до студентов. Всякая самостоятельная работа должна иметь методическое обеспечение, что подразумевает наличие достаточного количества методической литературы в библиотеке учебного заведения. Не менее важным условием выполнения самостоятельной работы является ее организация.

Обязательным условием рассматриваемого вида деятельности является учет ее результатов, проверка качества знаний и умений студентов, что приучает последних к выполнению заданий, формирует чувство ответственности, дисциплинированность. Анализ работы демонстрирует реальный уровень знаний и умений, дает возможность объективно оценивать достижения каждого студента.

Литература

Сомовол П.И. К проблемам дифференцированного обучения школьников //Математика в школе. 1991. №4.

Саранцев Г.И. Обучение доказательству //Математика в школе.1999. №6.

Селевка Г.К. Современные образовательные технологии: учеб. Пособие. М.: Нар. образ., 1998.