Педагогические науки/5. Современные методы преподавания

Учитель математики Ибрагимова Ф. А.

Средняя школа №29 имени Ю.А.Гагарина, г.Тараз, Казахстан

Дифференцированный подход при обучении математике

Если каждому отводить время,

соответствующее его личным

способностям, то можно обеспечить

гарантированное усвоение базисного

ряда школьной программы.

В последние годы значительно усилился интерес учителей общеобразовательной школы к проблеме дифференцированного подхода в обучении школьников математике на различных ступенях математического образования. Этот интерес во многом объясняется стремлением учителей так организовать учебно-воспитательный процесс, чтобы каждый ученик был оптимально занят учебно-воспитательной деятельностью на уроках и в домашней подготовке к ним с учетом его математических способностей и интеллектуального развития, чтобы не допускать пробелов в знаниях и умениях школьников, а в конечном итоге дать полноценную базовую математическую подготовку учащимся обычного класса. Такой организации обучения математике требует современное состояние нашего общества, когда в условиях рыночной экономики от каждого человека требуется высокий уровень профессионализма и такие деловые качества как предприимчивость, способность ориентироваться в той или иной ситуации, быстро и безошибочно принимать решение. Базовый курс математики призван служить одной из основ развития личностных качеств каждого отдельного ученика и подготовки его к жизни, предстоящей трудовой деятельности.

Математика объективно является наиболее сложным школьным предметом, требующим более интенсивной мыслительной работы, более высокого уровня обобщений и абстрагирующей деятельности. Поэтому невозможно добиться усвоения математического материала всеми учащимися на одинаково высоком уровне. Даже ориентировка на "среднего" ученика в обучении математике приводит к снижению успеваемости в классе, к издержкам воспитательного характера у ряда школьников (потеря интереса к математике, порождение безответственности, нежелание учиться и др.). Нынешнее отношение учащихся к математике характеризуется снижением ее популярности среди школьников.

Уровневая дифференциация выражается в том, что обучение учащихся одного и того же класса в рамках одной программы и учебника проходит на различных уровнях усвоения учебного материала. Уровневая дифференциация предполагает, что каждый ученик класса должен услышать изучаемый программный материал в полном объёме, увидеть образцы учебной математической деятельности. При этом одни учащиеся воспримут и усвоят учебный материал, предложенный учителем или изложенный в книге, а другие усвоят из него только то, что предусматривается обязательными результатами в качестве минимума. Каждый ученик имеет право добровольно выбрать уровень усвоения и отчетности в результатах своего учебного труда по каждой конкретной теме (разделу), а возможно и курсу в целом. Задачей учителя является обеспечение поступательного движения учащихся к более высокому уровню знаний и умений.

Принципы уровневой дифференциации:

1. Овладение обязательным уровнем подготовки.

2. Выделение и открытое предъявление всем участникам учебного процесса уровня обязательной подготовки.

3. «Ножницы» между уровнем обязательных требований и уровнем обучения (не ограничивать учебный процесс обязательными требованиями к результатам обучения).

4. Добровольность в выборе уровня усвоения и отчетности.

5. Соответствие содержания, контроля и оценивания знаний по уровневому подходу, в соответствии с которым контроль должен предусматривать проверку у всех учащихся достижений уровня обязательной подготовки. Это дополняется проверкой усвоения материала на более высоких уровнях.

Опыт показывает, что квалифицированная организация дифференцированного подхода в обучении математике требует огромных временных затрат при планировании и осуществлении учебного процесса. Поэтому учителю важно ознакомиться с уже имеющимся передовым опытом по составлению и использованию разноуровневых учебных задач для дифференцированной работы с учащимися. Руководствуясь теоретическими предпосылками, учитель сможет сам составить разноуровневые задачи по различным темам математических предметов.

Пытаясь создать образ ученика нашей школы, при внедрении дифференцированного подхода в обучении и воспитании учащихся, я исхожу из того, что нет и не может быть единых жестких требований к каждому ученику, так как нельзя оспаривать уникальную индивидуальность каждого человека. Тем не менее, основываясь на базовых ценностях и мисси школы, я попыталась «нарисовать» примерный образ ученика школы. В моём понимании, при использовании дифференцированного подхода ученик- это личность, максимально адаптированная к современным социальным условиям и ориентированная на успех.

Необходимость внедрения дифференцированного подхода на современном этапе подтверждается практикой: дети учатся самоорганизации, умению проводить самооценку. Происходит переосмысление их внутренней мотивации к обучению. Ученик становится активным участником педагогического процесса. Индивидуальное развитие ученика, его личная самооценка на каждом этапе урока формирует у подрастающего поколения стремление учиться по своему внутреннему убеждению.

Технология дифференцированного обучения способствует кардинальному изменению не только сознания ученика, но и сознания учителя. Дифференцированное обучение вдохновляет учителя на создание такого образовательного процесса, в котором ученик в самой жизни учится менять, улучшать, совершенствовать условия этой жизни, повышать её качество. Кроме того, на искусство нового мышления учителя оказывает влияние эмоциональная атмосфера в учебном заведении, его гуманитарная среда, что, конечно же, сказывается на познавательном выходе и продуктивности учебно-воспитательного процесса.

Примеры разноуровневых заданий.

Квадратичная функция

1-й уровень.

1. Дана функция: y=:

а) найти значения при y=8,

б) построить график заданной функции;

в) указать область значений и промежуток возрастания функции, используя построенный график;

г) решить неравенство .

2-й уровень.

2. Найти нули функции: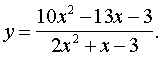

3. Дана функция :

а) построить график функции:

б) найти область значения и промежутки возрастания и убывания заданной функции, используя построенный график;

в) сравнить значение функции на концах отрезка [1;2].

4. Решить неравенство: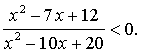

3-й уровень.

5. Найти область значений и промежутки возрастания и убывания функции не строя её графика.

6. При каких значениях график функции не пересекает ось абсцисс?

7. Построить график функции с помощью шаблона параболы , предварительно выделив квадрат двучлена.

8. Разложить трёхчлен на множители.

Методические рекомендации по реализации уровневой дифференциации

1. Использовать уровневый тематический контроль удобнее всего работая крупными блоками. В этом случае весь теоретический материал рассматривается компактно на первых уроках темы, а затем проводится отработка умений и навыков по уровням.

2. Содержание контролирующих работ должно быть заранее известно учащимся в той или иной форме. Открытость уровневых требований к учащимся, норм оценивания - важнейшее условие гуманизации обучения.

3. Сужение списка типовых задач обязательных для усвоения всеми учениками за счет исключения комбинированных, усложненных задач не означает снижения уровня преподавания математики. Изучение теоретического материала, разбор сложных, комбинированных задач должен проводиться в полном объеме, иначе учащиеся, способные усвоить математику на высоком уровне, не смогут пройти через полноценный учебный процесс.

4. Последовательное продвижение учащимися по уровням усвоения может осуществляться в индивидуальном для каждого ученика темпе. Для учеников, работающих в быстром темпе можно рекомендовать досрочную сдачу уровневых тестов.

5. Работая таким образом легко осуществить принцип добровольности в выборе уровня усвоения материала. Зная содержание знаний на всех уровнях, нормы оценивания на каждом уровне, ученик решает на каком уровне будет осваивать материал, какой отметкой ограничиться. В учебном процессе у учащихся формируются навыки планирования и регулирования своей деятельности. Ученик перестает быть пассивным наблюдателем и становится активным субъектом учебного процесса

6. Использование уровневого подхода дает возможность целенаправленно отбирать материал, планируя урок четко ставить цель достижения того или иного уровня и в соответствии с целью выбирать формы проведения учебных занятий.

7. Оценка должна отражать уровневый подход при контроле, в основе которого лежит достижение всеми учащимися минимального базового обучения. При этом достижение 1 уровня оценивается двухбалльной оценкой (зачтено -незачтено, верно-неверно и т.д.). Достижение учеником 2 уровня может оцениваться, исходя из отметки "4", и только при выполнении работы 3 уровня ученик может претендовать на отметку "5". Таким образом, оценка отражает уровень усвоения учеником материала.

8. Уровневый контроль, осуществляемый с помощью тестирования, завершается уровневой контрольной работой (тематической или итоговой).

Дифференцированный подход обеспечивает личностно – ориентированную дифференцированную среду для развития, воспитания и сохранения здоровья обучающихся.

Литература:

1. Давыдов В.В. Теория развивающего обучения. М,1996.

2. Дусовицкий А.К. Развитие личности в учебной деятельности. М., 1996.

3. Журнал «Математика в Школе» 1999 – 2005 гг.

4. Зотов Ю.Б. Организация современного урока/ Под ред. П.И. Пидкасистого. М., 1984.

5. Индивидуально-дифференцированный подход к обучению и воспитанию школьников (проблемы, поиск, опыт): Сборник статей. Орехово-Зуево, 2003.

6. Коротяев Б.И. Обучение – процесс творческий: Из опыта работы. М.,1980.

7. Научно-практический журнал «Завуч» 2004 – 2005 гг.