Физика/ 10. Физика полимеров

Богомолов В.Ю., д.т.н. Лазарев С.И., к.т.н. Вязовов С.А.

Тамбовский государственный технический университет, Россия

Расчет срока службы полимерной мембраны УАМ-150 при концентрировании подсырной сыворотки

Определим срок службы ультрафильтрационной ацетатцеллюлозной мембраны УАМ-150, производства ЗАО НТЦ «Владипор», в плоскокамерном баромембранном аппарате при ультрафильтрационном концентрировании подсырной сыворотки под вакуумом (давления с двух сторон мембраны соответственно равны 0,1 МПа и 0 МПа). Основная задача аппарата – это повышение качества и эффективности разделения подсырной сыворотки, за счет совмещения в нем мембранного концентрирования под действием избыточного давления или вакуума и деминерализации под действием электрического поля. Согласно расчетной схеме (рис.1) считаем, что мембрана уложена на металлическую сетку, жестко закрепленную по периметру. Металлическая сетка служит в аппарате опорой для мембраны и электродом.

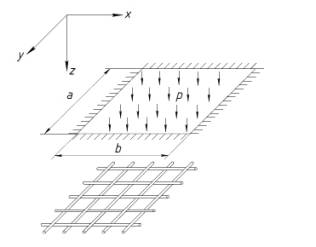
Рис.1. Расчетная схема

Под действием разделяемой среды происходит набухание мембраны, что значительно влияет на ее прочностные характеристики. При этом в процессе работы аппарата на систему действует рабочее давление p, вызывая прогиб мембраны в ячейки сетки-электрода и вызывая разрушающее воздействие контактных напряжений узлов сетки на поверхность мембраны.

Размеры сторон мембраны и в рассматриваемом аппарате соответственно равны 55 мм и 140 мм. Сила действующая на мембрану в таком случае равна

(1)

где F – сила, действующая на мембрану, Н; a и b – длины сторон мембраны, мм; p – рабочее давление в системе, МПа.

Вычисляем распределенную нагрузку на проволоку по наименьшей стороне ():

(2)

где q – распределенная нагрузка, Н/мм.

Для стальной проволоки диаметром 1 мм, максимальные контактные напряжения на ацетатцеллюлозную мембрану составят:

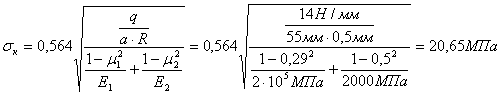, (3)

где R – радиус сечения проволоки, мм; и - коэффициент Пуассона для материала проволоки и мембраны соответственно; E₁ и E₂ – модуль Юнга для материала проволоки и мембраны соответственно, МПа. Материал проволоки – сталь: = 0,29; E₁ = 2·10⁵ МПа; мембраны - ацетат целлюлозы: = 0,5; E₂ = 2000 МПа.

Зная σ_к, можем определить время до разрушения мембраны [1]:

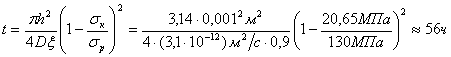, (4)

где h – толщина мембраны с учетом подложки, м; D – коэффициент диффузии разделяемой среды в материал мембраны, м²/с; ξ – коэффициент линейной аппроксимации; σ_р - напряжение разрушения материала мембраны, МПа.

Коэффициент линейной аппроксимации ξ может выбираться исходя из условий конкретной задачи. В данной работе коэффициент ξ принимался равным 0,9. Предел прочности для ацетата целлюлозы σ_р = 130 МПа [2]. Коэффициент диффузии D = 3,1·10^-12 м²/с был определен экспериментально.

Рассчитанное время до физического разрушения, как показывает практика, несколько ниже фактического, что объясняется меньшим влиянием набухания на материал мембраны. В случае набухания мембраны, в первую очередь происходит заполнение разделяемой средой пор, в отличие от волокнистых материалов, для которых выведена формула (4), где происходит проникновение жидкой фазы в волокна материала. Физически активная среда легко проникает в поры мембраны, обуславливая значительную диффузию, однако не снижает столь значительно прочность полимера. Этот фактор можно учесть, введя в формулу (4) эмпирический коэффициент.

Работа выполнена при поддержке ФГБУ «Фонд содействия развитию малых форм предприятий в научно-технической сфере».

Литература:

1. Степанов Р.Д., Шленский О.Ф. Расчет на прочность конструкций из пластмасс, работающих в жидких средах. – М.: Машиностроение, 1981. – 136 с.

2. Ярцев В.П., Киселева О.А., Сузюмов А.В. Прогнозирование прочности, деформативности и долговечности строительной фагнеры – Вестник Тамбовского государственного технического университета, т.14 (4), 2008. – с. 976 – 981.