Физика/2. Физика твердого тела

К.ф.-м.н. Чен Т.

Московский государственный университет тонких химических технологий имени М.В.Ломоносова, Россия

К динамической теории рентгеновского

спектрометра Гамоша

Рентгеновские спектрометры с вертикальной фокусировкой типа Гамоша [1-3] широко используются для рентгено-спектральных исследований кристаллов. Динамическая теория спектрометра Гамоша была рассмотрена в [4]. В настоящей работе представлено развитие динамической теории рентгеновского спектрометра Гамоша.

Используя общий формализм динамической теории дифракции рентгеновского излучения на изогнутых кристаллах [5,6], получим выражение для амплитуды дифрагированной волны в вакууме на расстоянии L_h от кристалла, изогнутого с радиусами кривизны R_x и R_y :

E_h (r_P) @ t^S (a_0x a_0ya_hx a_hy )^{- 1/2} g₀g_h sin² q_B [4p ² lL₀ L_h {(1 - g₀²)^1/2 g_h -

- g₀ (1-g_h²)^1/2 }] ^{- 1} ò dq_x G_h (q_x + q_0x )exp[iF₁ (q_x)] ò dq_yG_h (q_y)exp[iF₂(q_y)],(1)

где эйкональные функции в меридиональной и сагиттальной плоскостях:

F₁(q_x) = - q_x²(a_0x^{- 1}+ a_hx^{- 1} )/2æ + q_x (g_hx_P/a_hx L_h + g₀ x_S /a_0x L₀ ), (2)

F₂(q_y) = - q_y²(a_0y^{- 1} + a_hy^{- 1} )/ 2æ + q_y (y_P/a_hyL_h + y_S /a_0y L₀ ),

a_hx = g_h² /L_h + g_h /R_x , a_hy = 1/L_h + g_h /R_y .

t^S = - ir_e F(2q_B)NlP/sin q_B - коэффициент отражения идеальной (неизогнутой) отражающей атомной плоскостью, r_e = e² /mc² - классический электронный радиус, F- структурный фактор, N - число отражающих центров, приходящихся на единицу площади отражающей плоскости, e - заряд электрона, m - масса электрона, q_B - брэгговский угол, L₀ - расстояние от источника рентгеновской волны до кристалла, æ = 2p/l – волновое число, l - длина волны, r_P (x_P, y_P) – радиус- вектор точки изображения источника, r_S (x_S, y_S) – радиус-вектор точечного источника.

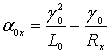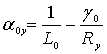, , (3)

G_h (q) = òò dr G_h0 (r)exp (iqr), (4)

G_h0 (r) - функция Грина, которую представим в виде произведения двух независимых функций Грина в двух перпендикулярных плоскостях: G_h0 (r) = G_h0 (x) G_h0 (y). Функция G_h (q) для совершенного кристалла, определяющая амплитуду отражения плосковолновой гармоники q, равна:

G_h(q) = 2i/{q+ (q² - 4p ² g₀² g_h²/L² [g_h(1 - g₀²)^1/2 - g₀ (1 - g_h ²)^1/2 ]² )^1/2 }.(5)

L = l | g₀ g_h | ^1/2 / P| c_h c_{- h}| ^1/2 - экстинкционная длина для совершенного кристалла, c_h и c_{- h} - фурье-компоненты рентгеновской восприимчивости, q_0x = p c₀ (g_h - g₀ )/l{(1 - g₀²)^1/2 g_h - g₀ (1 - g_h²)^1/2 }, g₀ и g_h - направляющие косинусы падающей и дифрагированной волн соответственно.

Вид функции G_h(q_y) и, следовательно, интеграл по q_y в (1), зависят от угловой расходимости падающего пучка в сагиттальной плоскости. В том случае, если величина y_i < y_eff (y_eff @ L_h| 2Dq cosq_B/{sinq_B - L_h ´ ´ (1 + sin² q_B)/R_y}|^1/2 - размер области полного брэгговского отражения вдоль оси y) , интеграл по q_y необходимо вычислять с конечными пределами от - q_{y, eff} до + q_{y, eff} , где q_{y, eff} @ æy_i /L₀ . При этом функция G_h (q_y ) = exp(j_y ), где фаза j_y в пределах угловой области полного отражения меняется от 0 до p. Положим приближенно, что внутри этой области фаза j_y линейно зависит от q_y . Тогда, если в фазе F₂ (q_y) исчезают квадратичные члены (условие фокусировки в сагиттальной плоскости), интеграл по q_y будет равен 2isin{q_{y, eff} a_0y^-1 ´(y_s/L₀-y_p/L_h + a_0y pL₀ /2æy_{e f f})}/{a_0y^{- 1} ´ (y_s/L₀ - y_p/L_h + a_0y pL₀ /2æy_{e f f})}. В работе [4] рассматривался именно этот случай. Однако, если y_i > y_eff , то G_h (q_y) имеет вид (5) и интеграл по q_y при выполнении условия фокусировки a_hy = - a_0y выражается через функцию Бесселя первого порядка.

Вертикальная фокусировка типа Гамоша происходит, если a_hy = - a_oy. В случае, если y_i < y_{e f f} , размер изображения источника вдоль оси Y равен:

Dy_p = lL_h /2y_e , y_e = y_i /|(1 – L₀ g₀ /R_y )|.

Рассмотрим спектральные свойства пучка, отраженного в схеме Гамоша, для случая y_i < y_{e f f}. Разложение излучения в спектр происходит вдоль оси X. Величина спектрального разрешения равна

dl/l = (a_0x^{- 1}+ a_hx^{- 1} ) |c_{h r}| (g_h + L_h /R_x )/{2sin² q_B (L₀ + L_h)},

где L_h ¹ - R_x g_h , a_0x^{- 1} ¹ - a_hx^{- 1} .

Спектральное разрешение для кристалла, изогнутого только в сагиттальной плоскости (т.е. R_x ®¥), равно

dl/l = |c_{h r}| (L₀ /g₀ ² + L_h /g_h ² )g_h/{2sin² q_B (L₀ + L_h)}.

В симметричном случае (g₀ = - g_h ) спектральное разрешение спектрометра Гамоша:

dl/l = |c_{h r}| /2sin³q_B .

Для отражения (220) CuK_a излучения от кристалла кремния (|c_{h r}| » 9´10^-6 , q_B = 23,65°) получаем следующую оценку спектрального разрешения dl/l ~ 7´10^-5 . В случае отражения (444) МоK_a излучения от кристалла кремния (|c_{h r}| » 9,4´10^-7 , q_B = 26,9°) имеем dl/l ~ 5´10^-6 .

Литература:

1. Von Hamos L. Roentgen spectra image by means of the crystal effect.//

Annalen der Physik.-1933.-Vol.17(6).-P.716-724.

2. Von Hamos L. Roentgen spectroscopy and diagram by means of curved

Crystal reflectors. II. Characterisation of a focusing spectrograph without Exact fissure decomposition.//Annalen der Physik.-1934.-Vol.19(3).- P.252-260.

3. Von Hamos L.Formation of true X-ray images by reflection on crystal

mirrors.//Z.Kristallogr.-1939.-Bd.101.-S.17.

4. Габриелян К.Т., Демирчян Г.О., Чуховский Ф.Н. Рентгеновские

спектрометры на отражение с вертикальной фокусировкой типа

Гамоша.//ЖТФ.-1990.-Т.60, Вып. 1.-С.170-178.

5. Габриелян К.Т., Чуховский Ф.Н., Пинскер З.Г. К построению

количественной теории фокусирующих рентгеновских

спектрометров с изогнутым кристаллом. I. Спектрометр на

отражение.//ЖТФ.-1980.-Т.50, Вып.1.-С.3-11.

6. Чуховский Ф.Н. Динамическое рассеяние рентгеновских лучей в

упруго изогнутых кристаллах. II. Брэгг-дифракция.//Металлофизика.-

1981.-Т.3, №5.-С.3-30.