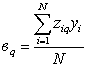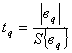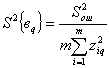Ахметов Жанболат Елемесович,

Сембаев Нурболат Сакенович,

Ыксан Жанар Мунсызбаевна

Павлодарский государственный университет имени С.Торайгырова, г.Павлодар Республика Казахстан

Оценка влияния основных параметров газоимпульсного прессового оборудования на качество изделий

Целью экспериментальных исследований является получение подтверждения результатов теоретических исследований, приведенных и реализация задач, поставленных в ходе выполнения работ в рамках госбюджетной программы.

Программа исследований была разработана в соответствии с поставленными задачами и на основании рекомендаций литературы по планированию экспериментов [1, 2, 3], которая содержала следующие этапы:

1) Разработка методики экспериментального исследования;

2) Подготовка объектов исследования и оборудования для проведения экспериментов;

3) Проведение экспериментов;

4) Обработка экспериментальных данных.

План экспериментальных исследований включает в себя следующие этапы:

1) Определение физико-механических свойств прессуемой смеси;

2) Определение погрешности измерений;

3) Составление регрессионных уравнений основных технологических параметров разрабатываемого оборудования.

1 Методика проведения экспериментальных исследований и подготовка объектов исследования и оборудования для проведения экспериментов

Для исследования газоимпульсного метода прессования была использована экспериментальная газоимпульсная прессовая машина (рисунок 1) [4]. Объем камеры сгорания – 0,15 м³, объем газового дозатора – 0,027 м³. Внутренний диаметр прессовой машины – 0,40м. Максимальный и минимальный ход поршня 0,70м и 0,35м соответственно. Подача и отвод форм осуществляется с помощью пластинчатого конвейера.

Последовательность технологических операций получения тротуарных плит из полусухой смеси газоимпульсным методом прессования следующее: под рабочий орган устанавливается форма (рисунок 2). Производится подача необходимой дозы смеси из бункера. Форма со смесью подается под рабочую насадку. Включается машина и приводится прессование смеси рабочим органом за счет импульса взрыва определенного стехиометрического состава газовоздушной смеси.

Мощность импульса J определяли по формуле [5]:

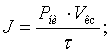(1)

где p – давление импульса нагружения, Н;

_τ – время нарастания давления импульса нагружения до максимума, с;

– объем камеры сгорания, м³.

После осуществления процесса прессования спрессованная форма отводится от установки и при помощи конвейера доставляется на следующий этап изготовления готовой продукции.

При проведении экспериментальных исследовании для фиксирования параметров и определения влияния различных факторов на качество изготовляемого изделия в соответствующих точках формы были установлены датчики регистрации скорости прессования смеси и нормальных давлений в прессуемой смеси. Сигналы с датчиков передавались на измерительный комплекс. По полученным результатам были построены графики зависимости.

После процесса прессования изготовленные изделия проверялись на прочность и плотность.

Эксперименты проводились на специальной тротуарной смеси следующего состава: цемент – 14%, песок – 46%, пластификатор – 12%, керамзит – 16% и специальные добавки – 12%. Влажность – 4…12%. Прочность на сжатие – 0,28…0,32 МПа.

Рисунок 1 – Общий вид экспериментальной установки

Рисунок 2 – Виды форм

2 Проведение экспериментов

Перед проведением экспериментальных исследований определены физико-механические свойства смеси. Для определения объемного веса смеси была изготовлена специальное приспособление Литвинова, после приготовления смеси определялись объемный вес, влажность, гранулометрический состав, вязкость, газопроницаемость, прочность на сжатие и на разрыв.

Определен погрешность измерений, где рассчитаны: коэффициент вариации, среднестатистическая ошибка, показатель точности измерений в процентах

2.1 Выбор основных параметров газоимпульсного прессового оборудования

Планирование многофакторных экспериментов – новый подход к организации и проведению экстремальных исследований сложных систем. Цель планирования эксперимента – извлечение максимума информации при заданных затратах на эксперимент либо минимизация затрат при получении информации, достаточной для решения задач. Планирование эксперимента позволяет соразмерить число опытов поставленной задаче.

Планирование многофакторных экспериментов с сокращением перебора вариантов является мощным средством повышения эффективности исследований и уменьшения затрат времени и средств на эксперимент.

2.2 Матрица планирования

С использованием кодированных значений –I, +I могут быть построены матрицы планирования , где - число возможных опытов.

Экспериментальные исследования проводились согласно условиям, приведённым в таблице 1.

Матрица планирования для четырех факторов представлена в таблице 3.1. Строки в столбцах х₁, х_2, х₃ и х₄ матрицы задают план эксперимента, то есть условия опытов, реализуемых при всех возможных комбинациях уровней факторов.

Матрица планирования составляется следующим образом: первая строка матрицы выбирается так, чтобы все изучаемые факторы находились на нижних уровнях, то есть ,. Образование всех последующих строк матрицы осуществляется так, чтобы при построчном переборе всех вариантов частота смены знака варьируемых факторов для каждого последующего фактора была вдвое меньше, чем предыдущего.

Таблица 1 – Значения факторов при экспериментах

Уровни варьирования	Значения факторов
	Площадь формы в свету		Насыпная высота		Вязкость смеси		Гранулометрический состав
	нат.	код.	нат.	код.	нат.	код.	нат.	код.
	S, мм^2	х1	h,см	х2	λ, МПа*с	х3	γ,мм	х4
Основной уровень	25000	0	14	0	20	0	2	0
Верхний уровень	40000	+ 1	18	+ 1	30	+ 1	3	+ 1
Нижний уровень	10000	– 1	16	– 1	10	– 1	1	– 1
Интервал варьирования	15000		2		10		1

Построенная по такому принципу матрица планирования для четырех факторов представлена в таблице 2.

Таблица 2 – Матрица планирования

Номер опыта	Факторы
	х0	х1	х2	х3	х4	х1х2	х1х3	х1х4	х2 х3	х2х4	х3х4
1	+1	-1	-1	-1	-1	+1	+1	+1	+1	+1	+1
2	+1	+1	-1	-1	+1	-1	-1	-1	+1	+1	+1
3	+1	-1	-1	-1	+1	+1	+1	-1	+1	-1	-1
4	+1	+1	-1	-1	+1	-1	-1	+1	+1	-1	-1
5	+1	-1	-1	+1	+1	+1	-1	-1	-1	-1	+1
6	+1	+1	-1	+1	+1	-1	+1	+1	-1	-1	+1
7	+1	-1	+1	+1	+1	-1	-1	-1	+1	+1	+1
8	+1	+1	+1	+1	+1	+1	+1	+1	+1	+1	+1
9	+1	-1	-1	+1	-1	+1	-1	+1	+1	+1	-1
10	+1	+1	-1	+1	+1	-1	+1	+1	-1	-1	+1
11	+1	-1	+1	-1	-1	-1	+1	+1	-1	-1	+1
12	+1	+1	+1	-1	-1	+1	-1	-1	-1	-1	+1
13	+1	-1	+1	+1	-1	-1	-1	+1	-1	-1	-1
14	+1	+1	+1	+1	-1	+1	+1	-1	+1	-1	-1
15	+1	-1	+1	-1	+1	-1	+1	-1	-1	+1	-1
16	+1	+1	+1	-1	+1	+1	-1	+1	-1	+1	-1

3 Регрессионные уравнения основных технологических параметров

3.1 Уравнение регрессии объема камеры сгорания

3.1.1 Рандомизация

Проведение любого эксперимента связано с ошибками, знание которых необходимо для результатов эксперимента. В связи с этим порядок проведения опытов должен быть выбран таким, чтобы имелась возможность оценить случайную ошибку эксперимента и избежать влияния возможных систематических ошибок.

Сделать случайными мешающие факторы, действие которых может иметь систематический характер, позволяет принцип рандомизации, который применяется при реализации матрицы планирования эксперимента.

Рандомизация заключается в случайной последовательности постановки опытов, запланированных матрицей. Для матрицы планирования 2⁴ (таблица 3.2) при трехкратном выполнении каждого (т=3) нужно провести 48 опытов. Используя таблицу случайных чисел выписывают числа от 1 до 48 с отбрасыванием уже выписанных чисел, например, 6, 2, 1, 7, и т. д. Эти числа заносят в матрицу планирования (таблица 4) и реализуют опыты согласно порядку записи этих чисел, то есть первым реализуем опыт № 3, вторым – опыт № 2 и т. д. При таком проведении опытов неучтенный фактор не будет вызывать систематической ошибки. Результаты каждого опыта записывают в столбцы таблицы 4 и производят их построчное осреднение

, (2)

где т – число повторных опытов, т обычно принимают равным трем.

3.1.2 Оценка воспроизводимости эксперимента

Прежде, чем приступать к определению модели эксперимента в виде уравнения регрессии, необходимо произвести проверку воспроизводимости эксперимента для исследуемого объекта.

Оценку воспроизводимости эксперимента проводят по критерию Кохрена G. Эксперимент считается воспроизводимым, если ,

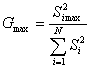(3)

где - оценки дисперсий в строках таблице 3, которые вычисляются по формуле

; (4)

- максимальная оценка дисперсии из всех полученных в таблице 3;

N – количество опытов в плане, N=16.

G_табл – табличное значение критерия Кохрена. Оно определяется по таблице 5 в зависимости от числа степеней свободы ν₁=т-1=3-1=2, количества выборок ν₂=Ν=16 и выбранной вероятности Р.

Для технических расчетов принимаем Р=0,95. Если проверка воспроизводимости эксперимента дала отрицательный результат, то эксперимент считается невоспроизводимым. Это возможно вследствие наличия в исследуемом объекте источников неоднородности (например, изменения температуры во время проведения повторных опытов, вязкости материала и т. д.).

Таблица 3 – Оценка дисперсии

Номер опыта	(уi1-i)^2	(уi2-i)^2	(уi3-i)^2	Дисперсия,
1	1650	1670	1700	422,9167
2	1750	1600	1750	500,0
3	1610	1710	1700	2022,917
4	1680	1660	1610	866,6667
5	1620	1630	1670	466,6667
6	1720	1710	1750	289,5833
7	1630	1690	1600	1400
8	1710	1680	1620	1400
9	1750	1700	1720	422,9167
10	1610	1700	1710	2022,917
11	1620	1630	1690	956,25
12	1750	1700	1680	866,6667
13	1700	1680	1630	866,6667
14	1650	1660	1600	689,5833
15	1690	1670	1620	866,6667
16	1750	1700	1610	3356,25

Таблица 4 – Матрица планирования

Номера опыта			Порядок реализации			Факторы											Плотность изделия, il			Среднее значение плотности, i	Среднее значение с учетом коэфф. регрессии, ŷi
						х0	х1	х2	х3	х4	х1х2	х1х3	х1х4	х2 х3	х2х4	х3х4
						Z0	Z1	Z2	Z3	Z4	Z5	Z6	Z7	Z8	Z9	Z10
1	17	33	10	25	40	+1	-1	-1	-1	-1	+1	+1	+1	+1	+1	+1	1650	1670	1700	1675	1479,063
2	18	34	41	26	11	+1	+1	-1	-1	+1	-1	-1	-1	+1	+1	+1	1750	1600	1750	1700	1880,625
3	19	35	12	27	42	+1	-1	-1	-1	+1	+1	+1	-1	+1	-1	-1	1610	1710	1700	1675	1865,625
4	20	36	43	28	13	+1	+1	-1	-1	+1	-1	-1	+1	+1	-1	-1	1680	1660	1610	1650	2299,688
5	21	37	14	29	44	+1	-1	-1	+1	+1	+1	-1	-1	-1	-1	+1	1620	1630	1670	1640	2314,688
6	22	38	45	30	15	+1	+1	-1	+1	+1	-1	+1	+1	-1	-1	+1	1720	1710	1750	1725	2733,75
7	23	39	16	31	46	+1	-1	+1	+1	+1	-1	-1	-1	+1	+1	+1	1630	1690	1600	1640	1862,813
8	24	40	47	32	48	+1	+1	+1	+1	+1	+1	+1	+1	+1	+1	+1	1710	1680	1620	1670	2293,75
9	25	41	2	17	1	+1	-1	-1	+1	-1	+1	-1	+1	+1	+1	-1	1750	1700	1720	1725	1083,125
10	26	42	33	18	3	+1	+1	-1	+1	+1	-1	+1	+1	-1	-1	+1	1610	1700	1710	1675	2733,75
11	27	43	4	19	34	+1	-1	+1	-1	-1	-1	+1	+1	-1	-1	+1	1620	1630	1690	1645	1883,438
12	28	44	35	20	5	+1	+1	+1	-1	-1	+1	-1	-1	-1	-1	+1	1750	1700	1680	1710	1464,375
13	29	45	6	21	36	+1	-1	+1	+1	-1	-1	-1	+1	-1	-1	-1	1700	1680	1630	1670	1449,375
14	30	46	37	22	7	+1	+1	+1	+1	-1	+1	+1	-1	+1	-1	-1	1650	1660	1600	1635	1015,313
15	31	47	8	23	38	+1	-1	+1	-1	+1	-1	+1	-1	-1	+1	-1	1690	1670	1620	1660	1451,875
16	32	48	39	24	9	+1	+1	+1	-1	+1	+1	-1	+1	-1	+1	-1	1750	1700	1610	1685	1897,813

Находим наблюдаемое значение критерия Кохрена – отношение максимальной исправленной дисперсии к сумме всех дисперсий (таблица 5):

Находим по таблице по уровню значимости 0,05, числу степеней свободы ν₁ =2 и количеству выборок ν₂ =16 критическую точку (0,05; 2; 16) = 0,2705.

Так как 0,054 < 0,2705 нет оснований отвергнуть нулевую гипотезу об однородности дисперсий. Другими словами, исправленные выборочные дисперсии различаются незначимо.

Таблица 5 – Значения критерия Кохрена при Р=0,95, α=0,05

Количество выборок, ν2	Число степеней свободы, ν1
2	0,9985	0,9750	0,9392	0,0957	0,8584
3	0,9669	0,8709	0,7977	0,7457	0,7071
4	0,9065	0,7679	0,6841	0,6287	0,5895
5	0,8412	0,6838	0,5981	0,5440	0,5063
6	0,7808	0,6161	0,5321	0,4803	0,4447
7	0,7271	0,5612	0,4800	0,4307	0,3907
8	0,6798	0,5157	0,4377	0,3910	0,3595
9	0,6385	0,4775	0,4027	0,3584	0,3286
10	0,6220	0,4450	0,3733	0,3311	0,3029
12	0,5410	0,3924	0,3264	0,2880	0,2624
15	0,4709	0,3346	0,2795	0,2483	0,2219
20	0,3894	0,2705	0,2326	0,2086	0,1814
∞	0000	0000	0000	0000	0000

3.1.3 Определение коэффициентов модели

После оценки воспроизводимости эксперимента переходим к определению коэффициентов уравнения регрессии.

Для матрицы планирования эксперимента 2⁴, приведенной в таблице 8, модель эксперимента записываем в следующем в виде

(5)

Определение коэффициентов уравнения регрессии (5) производится по формуле

; q=0…n, (6)

где – см. таблицу 3.3;

n – число коэффициентов.

3.1.4 Статистический анализ уравнения регрессии

Статистический анализ выше полученного уравнения регрессии включает проверку:

– значимости коэффициентов уравнения

– пригодности или адекватности полученного уравнения или описания процесса.

Проверка значимости коэффициентов проводится с помощью критерия Стьюдента.

, (7)

где - среднеквадратическое отклонение оценки коэффициентов.

(8)

Оценка дисперсии коэффициентов вычисляется с числом степеней свободы ν_в=N(m-1) по формуле

, (9)

где т – число повторных опытов;

N – число всех опытов в плане;

- дисперсия ошибки опыта

(10)

Таблица 6 – Значения критерия Стьюдента

t0	t1	t2	t3	t4	t12	t13	t14	t23	t24	t34
867,6454	4,103874	-4,53586	-0,64798	215,7774	1,511954	-1,94394	112,1006	-4,96785	-106,053	109,5086

Если величина больше значений t_крит, по таблице 6 для числа степеней свободы ν_в=N(m-1) и выбранной вероятности Р=1-α/2, то коэффициент в_q считается значимым. Здесь α – уровень значимости. Для технических расчетов α принимается равным 0,05. Если же t_q≤t_крит, то коэффициент в_q считают статистически незначимым. В этом случае фактор с незначимым коэффициентом может быть исключен из уравнения регрессии без пересчета остальных значимых коэффициентов.

В нашем случае исключаем значения - 0,64798, 1,511954 и - 1,94394 так как, они являются незначимыми.

Оцениваем неизвестное математическое ожидание при помощи доверительного интервала 0,95. Пользуясь справочника «Критические точки распределения Стьюдента» по α = 0,05 и N=16 находим t_γ = 2,12.

Находим доверительные границы для параметра – объем камеры сгорания:

Итак, с надежностью 0,95 неизвестный параметр α заключен в доверительном интервале 1673,326 < α <1674,174, так как 1673,326-1674,174=0,848.

Данный доверительный интервал присуще и для остальных факторов (вязкость материала, площадь формы в свету, фракция смеси) потому, что согласно Стьюденту второе слагаемое уравнения () применима для всех.

После исключения факторов с незначимыми коэффициентами производится проверка адекватности полученной модели.

3.1.5 Адекватность модели

Проверка адекватности полученной модели производится с помощью F– отношения (критерия Фишера)

, (11)

где - остаточная дисперсия, которая характеризует рассеяние результатов эксперимента относительно результатов (смотри таблицу 3), получаемых расчетом по модели:

(12)

где d – число оцениваемых коэффициентов в уравнении регрессии. Остаточная дисперсия определяется с числом степеней свободы ν_вст=N-d=16-11=5.

Так как значение полученного F – отношения меньше критического значения F_крит, выбранного по справочной таблице [6] для числа степеней свободы числителя ν_ост и знаменателя ν_ош=N(m-1) =16(4-1) =16·3=48 и выбранной вероятности Р=1-α=0,95, модель адекватно описывает процесс, то есть признается пригодной.

После чего с помощью найденных коэффициентов уравнения регрессии и исключения незначимых коэффициентов значимости составляем для нашего эксперимента уравнения регрессии.

У= + Х₁ Х₂ + Х₄+ Х₁₂ Х₁₃-

Х₁₄ Х₂₃ Х₂₄+ Х₃₄

Далее по такому же принципу составляем для выбранных технологических параметров уравнения регрессии

3.2 Уравнение регрессии длины хода штока

У=1670 - 2,5 Х₂ -11,2 Х₃+ 418 Х₄ +1,8 Х₁₃+ 208,5 Х₁₄ - 3,1 Х₂₃

- 208,1 Х₂₄+ 213,5 Х₃₄

3.3 Уравнение регрессии скорости прессования

У=1653-16,87 Х₂ -18,1 Х₃+ 418 Х₄ +3,1 Х₁₂ +3,5 Х₁₃+ 206,4 Х₁₄ +8,1 Х₂₃+ 210,6 Х₂₄ + 209,8 Х₃₄

3.4 Уравнение регрессии модуля упругости пружины

У= 1670-2,57 Х₁ +2,57 Х₂ -3,75 Х₃+ 408 Х₄ - 4,5 Х₁₂ +

+ 2,5 Х₁₃+ 211,2 Х₁₄ -7,9 Х₂₃ - 211,6 Х₂₄ + 208 Х₃₄

Выводы

1. Разработаны программа и планы проведения экспериментальных исследований и обработки результатов.

2. Создан измерительно-регистрирующий комплекс для фиксирования и определения необходимых параметров согласно плана экспериментальных исследований.

3. Для проведения экспериментов определены физико-механические свойства смеси.

4. Определены погрешности измерении при проведении экспериментальных исследований составляющие не более 10%. При таких показателях точности измерений надежность эксперимента считается обеспеченной.

5. Разработан план проведения экспериментальных исследований для определения основных параметров газоимпульсного пресса

6. Составлено уравнение регрессии для объема камеры сгорания.

7. Составлено уравнение регрессии для хода штока.

8. Составлено уравнение регрессии для скорости прессования.

9. Составлено уравнение регрессии для модуля упругости пружины.

Литература:

1. Спиридонов А.А. Планирование эксперимента при исследовании технологических процессов. М.: Машиностроение, 1981. – 184 с., ил.

2. Радченко Станислав Григорьевич, Устойчивые методы оценивания статистических моделей: Монография. – К.: ПП «Санспарель», 2005. – С. 504.

3. Гришин В.К. Статистические методы анализа и планирование экспериментов. Издательство МГУ им. Ломоносова, 1973.

4. Инновационный патент Распублики Казахстан №24366. Бекенов Т.Н., Ахметов Ж.Е., Абишев К.К., Богомолов А.В. Бюл.№8 от 15.08.2011 г.

5. Матвеенко И.В., Исагулов А.З., Дайкер А.А. Динамические и импульсные процессы и машины для уплотнения литейных форм.-Алматы:Ғылым,1998. – 345 с.ил.

6. Веденяпин Г.В. Общая методика экспериментального исследования и обработка опытных данных. – М.: Колос, 1973.