Технические науки/6. Электротехника и радиоэлектроника
Ст. преп.
Мирзакулова Ш.А.
Алматинский
университет энергетики и связи
СТАТИСТИЧЕСКАЯ ПРОВЕРКА
ГИПОТЕЗЫ О ВИДЕ ЗАКОНА РАСПРЕДЕЛЕНИЯ
В пакете Statistica исследовано эмпирическое распределение пакетов протокола
TCP (Transmission Control Protocol). Объем выборки 158 пакетов. При
этом рассмотрены интервалы между пакетами (157 интервалов) с целью оценки
степени согласия наблюдаемых данных с теоритическим экспоненциальным
распределением. На рисунке 1 представлены расчетные данные, полученные в
программном продукте Statistica.
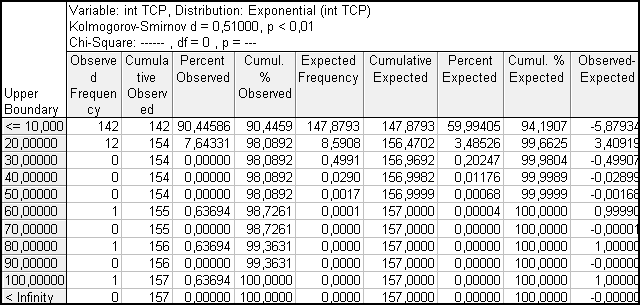
Рисунок 1 – Расчетные данные
пакета Statistica
На рисунке 2 представлен график, на
котором построена гистограмма ТСР с выравнивающей ее кривой экспоненциального
распределения. При этом в верхней части таблицы показано значение Dэксп = 0,42488
(максимальное расстояние между эмпирической и теоритической экспоненциальной
функциями) при экспериментально рассчитанном уровне значимости р<0,01 (очень
надежного).
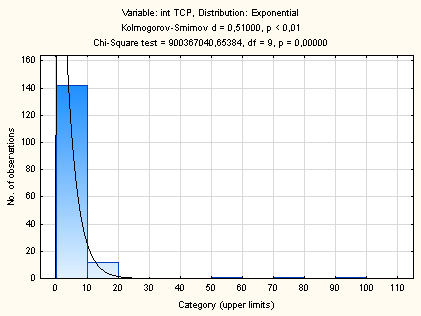
Рисунок 2 – Подгонка экспоненциального распределения
на распределение интервалов между пакетами ТСР
Форма гистограммы на рисунке 2 показывает,
что не точно распределение ТСР аппроксимировано экспоненциальным
распределением, которое отмечено красным цветом. Эмпирическое распределение
длиннохвостое распределение.
Одно выборочный критерий
Колмогорова-Смирнова в качестве меры расхождения между теоретическим и
эмпирическим распределениями рассматривает максимальное значение абсолютной
величины разности между эмпирической и теоретической функцией распределения.
Если D статистика Колмогорова-Смирнова
значима, то гипотеза о том, что соответствующее распределение экспоненциальное,
должна быть отвергнута. В специальной таблице «Критические значения критерия
Колмогорова-Смирнова при сопоставлении эмпирического распределения с
теоретическим» при объеме выборки 
и значении р=0,01
показано, что [1]
.
Выводы: так как 
больше 
, то гипотеза о достоверных
различиях принимается. Следовательно интервалы между пакетами ТСР не
распределены по экспоненциальному закону.
Литература:
1. Чубуков Ж. А., Угольник Т. С., Описательная статистика: учебно-методическое пособие для студентов всех факультетов медицинских вузов, аспирантов, магистрантов, соискателей и преподавателей. – Гомель: учреждение образования «Гомельский государственный медицинский университет», 2012. — 28 с.