Doctor of technical sciences, full professor, M.K. Shuakayev1
Ph.D, associate professor, S.T. Nazarbekova2
1Kazakh British Technical University, Kazakhstan
2Al-Farabi Kazakh National University, Kazakhstan
Working -
Out of Mathematical Nonlinear Models of
Theory of Dynamics Population
In control theory there are two concepts for describing
mathematical models of systems[1]. The first is the concept of "space of
states", which describes a system in the form of systems of ordinary or
stochastic differential equations. The second is Map "input-output",
describes the system as a series of Volterra in nonlinear case. Study of the
relationship between these concepts in various tasks is reflected in the works
[2-12].
In the study of theories of population dynamics, all models were considered
only in the concept of "space conditions". For example, examined
management issues not limited environmental objects[13]. In [14], differential
dynamics systems. .How to comment on works of theory of population dynamics, in
our view, that have not been received analytical decision systems.
Therefore, this work is devoted to the development of mathematical models
of population theories in the form of linear approximation deterministic model
using a nonlinear transformation of variables R. Brockett and linearization by
T. Karleman.
In [15] presented a specific biological example, model Mac Arthur, which is
a special case of model Rosenzveig W.L., Mac Arthur R.H., which under certain
assumptions the model is a special case of Kolmogorov, Kolmagorov A.N. from
1935, and published later in [16-18]. However, in General case, it has no place
Consider a model Rosenzveig
W.L., Mac Arthur R.H. [17], which is the next system
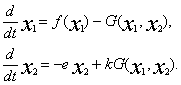 (1)
(1)
Let the polynomials ![]() and p
and p![]() resented in
the following form
resented in
the following form
![]() ,
, ![]()
![]() .
(2)
.
(2)
According to [15], polynomial ![]() system (1)
describes the rate of change of the number of victims
system (1)
describes the rate of change of the number of victims ![]() in the absence of predators, and polynomial
in the absence of predators, and polynomial![]() -intensity
predation, coefficients
-intensity
predation, coefficients ![]() -
efficiency ratios, making victims of predator and
-
efficiency ratios, making victims of predator and ![]() mortality in predator.
mortality in predator.
Note that the system (1)-(2)
is singular system of ordinary differential equations, which is, for example,
by the extremely narrow class of matrices of Drazin [19], using numeric
algorithms, but not the only way.. In the multidimensional case, when n is
solvable system, since there is no multiplication of vectors and this is the
main obstacle for her solution.
However, the problem of
stochastic bilinear filtering, where was a multi-dimensional system with
operation Kroneker product[20]. The authors intend to soon give the analytical
solution of the system already in operation.
Statement of the problem
For (1)-(2) we must build a linearized
model , retaining the original polynomial constant coefficients![]() ,
, ![]() and
and ![]() ,
, ![]() .
.
Theorem 1. For nonlinear deterministic system (1) - (2)
there is linearized, approximation model
![]() ,
(3)
,
(3)
Ãäå where
![]()
 ,
(4)
,
(4)
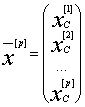 ,
,
The matrix ![]() contains all of the original coefficients of
polynomials
contains all of the original coefficients of
polynomials
![]() ,
, ![]() and parameters
and parameters![]() ,
, ![]() .
.
Proof: On the base of the method of nonlinear
conversion variables R. Brockett [21], we have 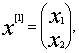
![]() - äâóõ ìåðíûé âåêòîð êîìïîíåíòû - 2-demensional vector of components
- äâóõ ìåðíûé âåêòîð êîìïîíåíòû - 2-demensional vector of components ![]() ,
,
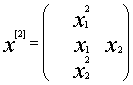 ,
, ![]()
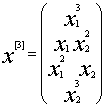 . (5)
. (5)
Through![]() , we denote
vector,
, we denote
vector, ![]() consisting
of all p-linear forms from
consisting
of all p-linear forms from![]()
Then using the (2) and (5) we get to system (1)
is equivalent to the following form
![]() .
( 6)
.
( 6)
Because
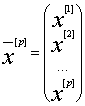 ,
,
we get the model of type
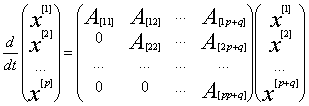 .
(7)
.
(7)
Matrixes ![]() of system (7), composed of the coefficients polynomials
of system (7), composed of the coefficients polynomials![]() and
and ![]() , defined by
(2) and parameters
, defined by
(2) and parameters![]() and
and ![]() .
.
Turning to the limit in (7) at
![]() û, we
obtain infinite dimensional system, that after linearization method of T.
Carleman, we have approximation model type (3) and (4) that in the end proves
our theorem[22]. On the base of theorems 1 we can build the linearized an
approximation model of system (3) - (4) for Lotka-Volterra models and
Kolmogorov.
û, we
obtain infinite dimensional system, that after linearization method of T.
Carleman, we have approximation model type (3) and (4) that in the end proves
our theorem[22]. On the base of theorems 1 we can build the linearized an
approximation model of system (3) - (4) for Lotka-Volterra models and
Kolmogorov.
Example 1. For illustration purposes, the application of the
theorem 1 demonstrate its use on Mac Arthur
model.
Due to the fact that this model presented in [4] is 2 - dimensional, we
have every reason to rewrite it as follows
![]() (8)
(8)
![]() .
.
According to [4], the system (8), ![]() means biomass of two species of insects. To
update the values of the members of the right-wing parts of the equations,
consider it relative
means biomass of two species of insects. To
update the values of the members of the right-wing parts of the equations,
consider it relative![]() .
.
Insect of larvae ![]() are eaten by larvae
are eaten by larvae![]() ( member +
( member +![]()
![]() ), but adults are eaten by larvae
), but adults are eaten by larvae ![]() species of larvae
species of larvae ![]() at condition to a high number of species
at condition to a high number of species ![]() or
or ![]() , or of both types (members-
, or of both types (members-![]() ).
).
At low![]() mortality
rate
mortality
rate![]() of higher
than its natural growth (
of higher
than its natural growth (![]()
![]() ).
).
(![]()
![]() ).
).
In the second equation ember reflects the natural growth of the species![]() , -
, -![]() - the self-restraint of this species, the larvae -
- the self-restraint of this species, the larvae -![]() of insect eating species by eating insect larvae look like adults
of insect eating species by eating insect larvae look like adults![]() . According to the theorem 1, the equation system
(3) shall conform to the following ratios:
. According to the theorem 1, the equation system
(3) shall conform to the following ratios:
![]() , (9)
, (9)
![]() , (10)
, (10)
![]() (11)
(11)
At ![]() , we have
, we have
![]()
-![]()
![]()
![]() (12)
(12)
At ![]() , we have
, we have
![]()
-![]() . (13)
. (13)
Check the
accuracy formulas (10), when ![]()
![]() (
(![]()
![]() )
)![]() +
+
(![]()
![]() )
) ![]() . (14)
. (14)
Producing
similar on the right side of (14), we obtain the formula (11) at ![]() .
.
Elements![]() of the system (6), are calculated
using formulas (8) -(13) in the following form
of the system (6), are calculated
using formulas (8) -(13) in the following form
![]()
![]()
![]() ,
,
![]()
 ,
,
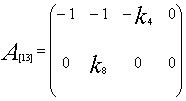 ,
,
![]()
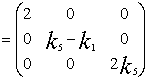 ,
,
 ,
,
 .
.
Still, you can get all the
parameters of the model for approximation system (7).
As noted in [4], that the
model of Mac Arthur [5] helps to answer the question: how should impact the bio
enosis, manage to quickly destroy the harmful kind. In [4] assumes that the
population of harmful species is compatible with surrounded of biocenoses. The introduction of management functions in the
system of equations (1) may be in two forms. First, you may enter the control
parameters that define the kind of features and. This is consistent with the
use of a biological control, changing the character of interaction between
populations.
Secondly, the authority may be confined to a brief, dramatic changes in
variables and functions. This is a one-time destruction techniques for either or
both populations of chemical means. From the formulated above shows that
approval for the joint of the second method is ineffective, while changing the
kinds of functions and can lead to the desired result is the destruction of
populations of harmful type. It is interesting to note that sometimes effects
to apply not to the pest, but to his partner.
Some of the ways to be more efficient in General can be said. It depends on
the available means of control and of an explicit type functions and describing
interaction between populations of researched conenoses. In connection with the
aforementioned comments from [4], you can enter in future the classes of linear or bilinear deterministic and
stochastic systems, based on the original system (6). In nonlinear
deterministic and stochastic cases, they are described as an infinite uniformly
convergent Volterra’s series. We note, that this work corresponds to the
theoretical direction of research, it would be interesting to solve the
following problems in the future for the dynamics of populations. The problem
of Realization. Let the mean kernel
type known deterministic or stochastic systems. We must to defined parameters
of the original system.
Problems of the structural and
parametric identification. Let the known values of the input and output of the system. We must to
defined firstly structure and parameters of the original system. Solution of
Realization Problem, structural and
parametric identification are members assigned with the biological meaning,
here we see a modern development of the theory of mathematical models of
ecological systems. This paper investigates the problem of finding the
analytical solutions to mathematical models of the dynamics of populations, due
to the use of classical methods of management theory, which undoubtedly will
make a definite contribution to and enrich the scope of this direction, and it
is the nature of the theoretical result. The authors working - out algorithm
representation of two-dimensional approximation models using a nonlinear
transformation of variables and linearization of T. Karleman. The results are illustrated on the biological model
of Mac Arthur [16].
Theory models for future studies, we can propose of another classes of
bilinear, deterministic and stochastic systems, and also made mathematical
problems of setting structural and parametric identification for the dynamics
of populations.
References
1.
Assaubayev K/Sh., Shuakayev M.K.
Voterra`s Series and Theory of Control, Alma Ata, (in russion), 167 p., 1993.
2.
Volterra V. SopraleFuzionicheDipendone de AltreFunzioni.
Ren.R. Academia deiLincei 2 Sem. p.p. 97 – 105, 141 – 146 and 153 – 158, 1887.
3.
Volterra V. Leconssur les Fonctionc De Lignes. Paris.
France: Gaunthier – Villars, 1913.
4.
Kalman R.E. Math. Description of Linear Dynamical Systems. – J. Control
(SIAM), 1 (1963), p.p. 152 – 192.
5.
Popkov Y.S. Funkcionalnii ryadi v
teorii upravlyaemih dinamycheskih ñèsystemñòåì. – Ì. 1976. 257s.
6.
Popkov Y.S., Kiselev Î.N., Petrov Î.R., Shmulyan B.L. Identifikaciya I optimizaciya nelineinih
stohasticheskih system. – Ì.: Energiya, 1976. – 444 s.
7.
Bruni C., Di`Pillo C., Koch G. On
the Mathematical Models of Bilinear
Systems. Ricerche di Automatica, 1971, v.2, n.1.
8.
D`Allesandro P., Isidori A., Ruberti
A. Realization Structure Theory of Bilinear Dynamical Systems. – Ins. Automat.
Univ. of Rome, Rome., 1974, Italy,
Rep.2 – 04 and 2 – 06.
9.
Isidori A. Direct Construction of
Minimal Bilinear Realizations from Nonlinear Input – Output Maps . –
IEEE TR. Aut. Contr., 1973, AC – 18,
n.6, Dec.
10.
Gilbert E.C. Controllabity and
Observability in Multivariable Systems. – J.Control (SIAM), 1963, n. 1, p.p.128
– 151.
11.
Gilbert E.C. Functional Expansions
for the Response of Nonlinear Differential Systems. – IEEE TR. Aut. Contr.,
1977, v. AC – 22, n.6, Dec.
12.
Brockett R.W. Nonlinear Systems and
Differential Geometry. Recent trends
in system theory. Proc. IEEE, vol.64, no. 1, pp. 61–72, 1976.
13.
Zaslavskii B.G.,, Poluektov R.
Upravlenie ecologicheskimi systemamy. Ì. Nauka.- 1985. 181 s.
14.
Kashyap R.L., Rao A.R. Postroenie
dinamycheskih stohostocheskih modelei po experimentalnim denim. Ì. Mir.- 1983.384 s.
15.
Rubin A.B., Pyteva N.F.,
Reznitchenko G.Y.,. Mathematical models of Biological Production processes.
Moscow: Moscow State University, 304 h., 1987.
16.
Mac Arthur R. Graphical
analisys of ecological systems. Division of Biology Report.- Prinston, 1971.
17.
Rosenzveig W.L., Mac Arthur R.H. Graphical
representation and stability conditions of predator –prey interactiens. Amer.
Nature.- 1963/-Vol.97, p.p. 209-223.
18.
Kolmogorov A.N. kachestvennoe izuchenie
modelei dinamiki populyacii. Problemy kibernetyki. Vip. 25. Ì., 1972. 241s.
19.
Brockett R.W. Volterra
Series and Geometric Control Theory. Automatica.Vol.12, Pergamon Press, 1976.
pp.167-176.
20.
Carravetta, F., A.Germani, M.Shuakayev. A New Suboptimal Approach to the Filtering
Problem for Bilinear Stochastic Differential Systems. SIAM J. Control Optim.,v.38, ¹ 4, 2000. pp. 1171-1203
21.
Campbell S.L. Singular system of differential
equations. San Francisko: Pitman.1982
22.
Carleman T.
Application de la theorie des
equations integrals singulieres aux equations differentiallies de la dynamique/
T.Ark. Mat.Astrom. Fys.22 R.1 1932