Д.э.н., проф. Дроговоз П.А., Шиболденков
В.А.
МГТУ им. Н.Э. Баумана, Россия
Нейросетевое картирование показателей
деятельности
предприятия как средство поддержки принятия решений
Финансовые данные являются основой феномена Big data: информации действительно много, она разного качественного состава, имеет протяжённость по источникам, по объектам, по факторам и по времени. Для решения такого рода задач: поиска в огромном и сложном наборе важных и полезных знаний, применяют особые математические механизмы, которые относят к обширной категории методов интеллектуального анализа данных (ИАД). Один существенный плюс экономических данных в их природе: они содержаться в цифровой форме, которая позволяет оперативно работать с ними на компьютере, минуя фазы сбора и предобработки, присущие другим областям науки.
Когда количество исследуемых параметров преодолевает значение 3D, нам становится тяжело отобразить законы многомерного мира. Для этого применяют некоторые упрощения или ухищрения. Но упрощения, это по сути отказ от некоторых факторов, которых не всегда правомерен и полезен, а во-вторых порождает неточную математическую модель. К ухищрениям относятся способы сокращения размерностей или применение проекций. Но этот принцип позволяет нам лишь чуть-чуть завысить планку работы с многомерным «миром». К примеру, если у нас 20 значимых факторов, то простое их попарное сравнение создаст почти 200 зависимостей. Адекватной работы с таким набором всё равно не получится. Для более результативной работы применяют разные методы визуального представления и визуального анализа Больших данных. К данной категории относится большой класс представителей такого вида «мягких вычислений», как искусственные нейронные сети.
Нейросеть можно представить в виде ориентированного графа, где узлы составлены нейронами, а связи между ними обладают весовым коэффициентом. Данный математический метод, подражает биологическому устройству человеческого мозга и копирует его преимущества при создании нейрокомпьютерной техники: в мозге присутствует особый молекулярный механизм, который оценивает не только время поступления сигналов на синапс, но и их количество, и группировку (паттерн) [4].
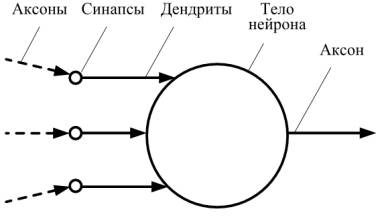
Рисунок 1. Принципиальная схема нейрона
Мозг человека – связанная структура из мозговых клеток, называемых нейронами. Между нейронами есть связи-синапсы, осуществляющие регулируемую и управляемую передачу сигналов между клетками. Формализуют их с помощью веса связей, т.е. выражения их значимости и эффекта (возбуждения или торможения). У нейрона один выход-аксон, которым передаёт сигнал далее к любым другим нейронам.
Качественное отличие нейросетевого подхода от других – это возможность научиться выполнять задание, а не выполнять конкретную, заранее предопределённую программу, и даже исправить возникающие в процессе работы ошибки. Искусственные нейронные сети (ИНС) относятся к мягким методам интеллектуального анализа, т.е. к таким методикам, которые могут работать с неявной, неполной информацией, содержащие пропуски и ошибки.
Среди обширного класса нейронных сетей есть особо удобный метод нейрокартирования по принципу Кохонена, который существенно выделяется из прочих алгоритмов ИНС [1,2,3].
Нейросеть данного типа обладает способностью к самоорганизации, что означает её работу без влияния учителя. Это в свою очередь позволяет выполнять в автоматическом (или автоматизированном) режиме сложный и тяжёлый этап обработки входной, или другими словами сырой, информации. Также отсутствие предустановок позволяет избегать ошибок априорного суждения о результатах кластеризации и нахождении неожиданных, скрытых закономерностей.
Этот метод называют картированием неслучайно – результатом работы нейронной сети является карта (а если сказать строже картограмма), т.е. визуальное отображение найденных закономерностей в самом геометрическом расположении объектов. Такая манера визуального исследования в разы удобнее сложного и ненаглядного аппарата традиционной статистики, и прочих аналитических математических методов. Полученный результат интерактивен: с ним можно плодотворно работать впоследствии, детально изучать особенности в расположении данных, причём в виде интуитивно понятных изображений.
Метод очень эффективен при работе с многомерными данными. Самоорганизующиеся карты не только анализируют зависимость от нескольких факторов сразу, но и сводят это к специальной группировке объектов, традиционно к двумерному расположению, где учтены все закономерности в данных, но размерность сокращена до приемлемой для человеческого восприятия.
Работа с SOM требует минимальных знаний математики и программирования, не нужна специализированная подготовка (для конечного пользователя) [4,5].
Если провести
математическую аналогию, то принцип построения узлов самоорганизующейся карты
Кохонена является близкой к регрессионному анализу, но с возможностью
нелинейного визуального проецирования результата. В обоих случаях пытаются
последовательными приближениями (аппроксимациями) сформировать аналитическую
функцию из простого набора, близкую к реальному объекту. В методе
среднеквадратической ортогональной регрессии находят самую «приближённую»
функцию (а для SOM
топологию узлов) к изучаемой экспериментальной зависимости. Причём мера
расстояния выбирается именно ортогональной, что аппроксимирует к ближайшей
точке кривой, чтобы полученная фигура была сглаженной [1,2].
Для задач
разведочного анализа конечно же неизвестны ожидаемые закономерности в данных, и
поэтому применяются методы гибкой аппроксимации, когда никакие априорные
параметры не вводятся в модель. Для самоорганизующейся карты находят набор
дискретных данных, олицетворяющих узлы, которые представлены своими векторами,
составленными из переменных геометрического положения и весовых коэффициентов
связей между нейронами. Такая «цепная» конструкция из дискретных, но связанных
между ячеек, эффективнее, с более плавным движением, так как когда узел
перемещается, он тянет за собой именно соседние узлы, и как уже писалось выше,
на каждой итерации «подтяжка» соседей будет происходить на всё меньшее и
меньшее расстояние. Цепная модель
позволяет избавиться от части топологических проблем традиционных методов,
таких как зигзаги, петли, и прочие спутанности непрерывных кривых. Для
формализации описанного процесса используют меру соседства, некую монотонно
убывающую от времени функцию, выражающую влияние на соседей.
С полученным геометрическим результатом работы карты Кохонена можно работать далее. В первую очередь стоит проанализировать компонентные плоскости, которые являются своего рода срезами по одному выбранному параметру из всего многомерного множества, а проще говоря это проекции, помогающие отразить на полученной карте рассматриваемый в данный момент отдельный фактор [6,9]. Для этой процедуры формируют цветовую палитру, простой градиентный метод раскраски, который превращает полученную карту в «тепловую», другими словами у карты появляется третье измерение (для выбранного параметра), выраженное интенсивностью цвета [1,6].
Компонентная плоскость – это инструмент интерактивного анализа данных, позволяющих формулировать визуальное суждение о закономерностях в данных, как по отдельным параметрам, так и в множественном рассмотрении, и наглядно видеть связь между факторами, характер их взаимоотношения. Группа компонентных плоскостей формирует целый компонентный «атлас», удобно рассматривая который можно оценивать влияние всех параметров одновременно. Визуально такой атлас значительно проще рассматривать, чем такой же объём диаграмм или графиков рассеивания [7,8,9].
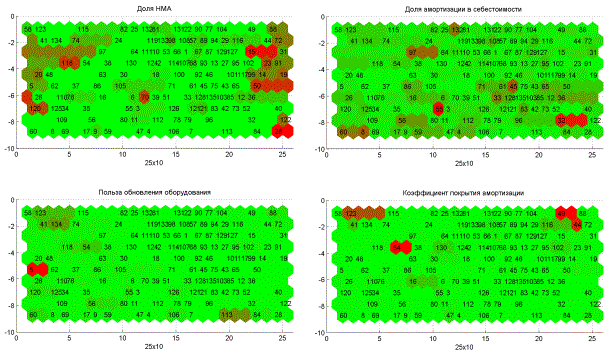
Рисунок 2. Пример нескольких компонентных плоскостей
Второй путь для аналитики полученных закономерностей – анализ кластеров и их границ. Для такой задачи существует своя процедура построения особой U-матрицы (unified distance matrix), которую мы будем называть картой кластеров. На деле это такая же картограмма (матрица с некоторыми геометрическими закономерностями), но на ней указаны узлы, связывающие нейроны между собой, причём эти узлы окрашены в такую палитру, чтобы визуально олицетворять «пропасть» между непохожими объектами [1,2]. Эти разноцветные границы подчёркивают очертания кластеров, а также указывают на их групповую близость.
На полученную карту данных можно наносить любую важную информацию, будь то подписи, легенды, замечания, инфографические маркеры и прочие атрибуты [1,6]. Глядя на «геометрический» результат можно увидеть новые закономерности, заполнить недостатки в информации и заметить тренды будущих изменений.