ПРОБЛЕМЫ
МОДЕЛИРОВАНИЯ ФИНАНСОВОЙ УСТОЙЧИВОСТИ СТРАХОВЩИКОВ В ОБЩЕМ СТРАХОВАНИИ
Рыжков О.Ю.,
к.э.н, научный консультант
Сибирская
межрегиональная ассоциация страховщиков
Показано,
что в общем страховании ни для одного из известных способов обеспечения
финансовой устойчивости страховщиков не имеется моделей, гарантирующих заданный
уровень финансовой устойчивости. Предложена концепция обобщенного актуарного
базиса, единого для страхования жизни и общего страхования. В рамках данной
концепции разработан комплекс моделей расчета страховых тарифов,
резервирования, определения достаточности собственного капитала и деления
риска, который в рамках имеющейся информации обеспечивает заданную вероятность
неразорения (надежность) страховщика как меру его финансовой устойчивости.
Статья 25 Закона РФ «Об организации
страхового дела в Российской Федерации» [2] предусматривает следующие способы
обеспечения (гарантии) финансовой устойчивости страховых организаций:
-
экономически
обоснованные страховые тарифы;
-
страховые резервы,
достаточные для исполнения страховщиком принятых на себя обязательств;
-
собственный капитал;
-
перестрахование.
Как ни парадоксально, но, по крайней мере,
в общем страховании[1] отсутствует
достаточный арсенал научно обоснованных моделей, позволяющих для каждого из
перечисленных способов определить такие суммы или ставки, которые обеспечивают
требуемый уровень финансовой устойчивости.
Так, официальная методика расчета
страховых тарифов в общем страховании [4] применима только к простейшим
ситуациям, когда вероятность наступления страхового случая не изменяется в
течение срока страхования, вероятность наступления более чем одного страхового
случая в течение срока страхования является практически невозможным событием, а
страховые суммы по договорам страхования почти одинаковы. При этом в целом ряде
видов страхования (медицинское страхование, страхование ущерба в автомобильном
транспорте и т.п.) в течение срока действия договора страхования может произойти
несколько страховых случаев (особенно если договор заключается не на один год),
а вероятность наступления страхового случая меняется со временем [10,11].
Страховой портфель часто бывает неоднородным, и условие о практически
совпадающих страховых суммах не выполняется. В общем страховании все чаще
встречаются многолетние договоры, но официальная методика не учитывает
изменения ценности денег во времени.
Сказанное целесообразно проиллюстрировать
на примере конкретного страхового риска, характеристики которого (так
называемый актуарный базис) являются вполне обычными для страховой практики и
представлены в
таблице 1.
Таблица
1 – Актуарный базис страхового риска
|
Параметр |
Значение |
|
Страховой
риск |
«Ущерб
автотранспортному средству (в страховании каско)» |
|
Единица
измерения времени |
Год |
|
Срок действия
договора страхования |
3 |
|
Срок действия
страхования |
3 |
|
Выжидательный
период |
0 |
|
Отсрочка начала
страховых взносов |
0 |
|
Рассрочка
страховых взносов |
0 |
|
Отсрочка начала
страховых выплат |
0 |
|
Рассрочка
страховых выплат |
0 |
|
Учитывать
возраст объекта |
ИСТИНА |
|
Начальный
возраст объекта страхования |
0 |
|
По договору
возможен только один страховой случай |
ЛОЖЬ |
Таблица 1 (продолжение)
|
Параметр |
Значение |
|||
|
Сумма убытка в
относительных единицах к страховой сумме |
ЛОЖЬ |
|||
|
Интенсивность
наступления страхового случая в единицу измерения времени |
нижняя граница возраста (не
включая) |
верхняя граница возраста
(включая) |
интенсивность наступления
страхового случая в единицу измерения времени |
|
|
0 |
1 |
0,0350 |
||
|
1 |
2 |
0,0450 |
||
|
2 |
3 |
0,0550 |
||
|
Интенсивность
наступления отменительного события в единицу измерения времени |
0 |
|||
|
Начальная
страховая сумма, руб. |
нижняя граница интервала |
450000 |
||
|
верхняя граница интервала |
1150000 |
|||
|
вероятность попадания в
интервал |
1 |
|||
|
Сумма
убытка, руб. |
нижняя граница интервала |
50000 |
||
|
верхняя граница интервала |
1150000 |
|||
|
вероятность попадания в
интервал |
1 |
|||
|
Уровень начальных
переменных расходов на ведение дела от брутто-премии (агентское
вознаграждение), отн. ед. |
0,10 |
|||
|
Уровень равномерных
переменных расходов на ведение дела от брутто-премии (текущие расходы страховщика),
отн. ед. |
0,1275 |
|||
|
Уровень переменных расходов
от поступивших страховых взносов, отн. ед. |
0 |
|||
|
Уровень переменных расходов
от суммы убытков, отн. ед. |
0,03 |
|||
Таблица 1 (продолжение)
|
Параметр |
Значение |
|
Сумма постоянных расходов
на ведение дела, руб. |
0 |
|
Сумма постоянных расходов
на ведение дела |
0 |
|
Ставка доходности, годовых |
0 |
|
Надежность |
0,95 |
|
Число договоров в портфеле |
100 |
|
Период
запаздывания убытков |
91/365 |
У данного страхового риска имеется
вариация страховых сумм, договор страхования заключен на 3 года с различной
вероятностью наступления страхового случая, убыток от наступления страхового
случая составляет величину, не меньшую 50000 рублей и ограниченную страховой
суммой по конкретному договору страхования.
Кроме того, по одному договору возможно наступление нескольких страховых
случаев.
При расчете страховых резервов по общему
страхованию предусматривается директивное увеличение произошедших, но неурегулированных
убытков на 3% (то есть уровень таких расходов составляет 0,03 от суммы убытков)
– расходы на урегулирование [6]. Данная величина предусмотрена в таблице 1.
Общая нагрузка страховщика, включающая в себя все виды расходов, составляет
0,25 от страховой брутто-премии. Действительно, справедливо тождество:
0,1+0,1275+(1-0,25)*0,03=0,25.
Период запаздывания убытков (время между
наступлением страхового случая и его урегулированием) составляет 91день (91/365
года).
По данным актуарного базиса рассчитан страховой
тариф с применением официальной методики (таблица 2).
Для расчета в таблице 2 использован
актуарный базис из таблицы 1, распределение заданных в нем случайных величин
принято равномерным, что полностью согласуется с таблицей 1. Вероятность
наступления страхового случая определена по формуле сложения вероятностей трех
совместных независимых событий, состоящих в наступлении страхового случая
соответственно в первый, второй и третий годы срока действия договора страхования.
Таблица
2 – Расчет страхового тарифа и страховой премии по официальной методике
|
Показатели |
Значение |
|
Количество
договоров |
100 |
|
Средняя
страховая сумма по 1 договору, руб. |
800 000 |
|
Вероятность
наступления страхового случая по 1 договору в год, доли ед. |
0,1291 |
|
Средний
убыток по одному страховому случаю, руб. |
600 000 |
|
Среднеквадратическое
отклонение убытка по одному страховому случаю, руб. |
317 543 |
|
Вероятность
неразорения (надежность) страховщика, доли ед. |
0,95 |
|
Нагрузка,
отн. ед. |
0,25 |
|
Страховой
тариф брутто, отн. ед. |
0,1925 |
Таблица
3 – Результаты статистического моделирования страховых портфелей
|
Номер попытки |
Математическое
ожидание страховых выплат по портфелю, руб. |
Среднеквадратическое
отклонение страховых выплат по портфелю, руб. |
Средняя
начальная страховая сумма по портфелю, руб. |
Дисконтированная
страховая нетто-премия по портфелю, руб. |
Дисконтированная
страховая брутто-премия по портфелю, руб. |
Страховой тариф
брутто, доли ед. |
|
1 |
9 418 837 |
2 591 966 |
80 136 945 |
10 232 682 |
13 643 576 |
0,1703 |
|
2 |
9 430 700 |
2 755 278 |
79 928 178 |
10 390 932 |
13 854 575 |
0,1733 |
|
3 |
9 359 554 |
3 033 115 |
80 001 788 |
11 163 128 |
14 884 171 |
0,1860 |
|
4 |
9 207 277 |
2 697 469 |
79 700 634 |
10 291 827 |
13 722 437 |
0,1722 |
|
5 |
9 414 365 |
3 060 851 |
79 969 068 |
10 816 366 |
14 421 821 |
0,1803 |
|
6 |
9 281 931 |
2 988 638 |
80 176 001 |
10 869 063 |
14 492 083 |
0,1808 |
|
7 |
9 851 421 |
2 661 376 |
80 102 133 |
10 120 576 |
13 494 101 |
0,1685 |
|
8 |
9 894 392 |
2 992 386 |
80 083 028 |
10 910 602 |
14 547 469 |
0,1817 |
|
9 |
9 661 150 |
2 895 140 |
80 072 695 |
10 513 048 |
14 017 398 |
0,1751 |
|
10 |
9 636 762 |
2 963 117 |
80 092 642 |
10 805 027 |
14 406 703 |
0,1799 |
|
Среднее |
9 515 639 |
2 863 933 |
80 026 311 |
10 611 325 |
14 148 433 |
0,1768 |
|
Коэфф.
вариации |
0,025 |
0,060 |
0,002 |
0,033 |
0,033 |
0,032 |
Официальная методика декларирует, что при
применении страхового тарифа, рассчитанного в соответствии с ней, сумма
страховых выплат с вероятностью, равной заданной величине надежности, не
превысит сумму страховой нетто-премии по портфелю.
Однако с применением алгоритма, указанного
в [12], проведено статистическое моделирование страховых портфелей. Произведено
в общей сложности 10 попыток, в каждой из которых получена статистика по 100
страховым портфелям со свойствами, указанными в таблице 1.
Результаты статистического моделирования
представлены в таблице 3.
Сравнение результатов оценки страховых
премий и страховых тарифов по официальной методике со средним результатом
статистического моделирования по всем попыткам приведено в таблице 4.
Таблица
4 – Сравнение страховых премий и страховых тарифов с результатами
статистического моделирования.
|
Показатели |
Официальная методика |
Имитационное моделирование |
|
Математическое ожидание страховых выплат по портфелю, руб. |
7 746 698 |
9 515 639 |
|
Среднеквадратическое отклонение страховых выплат по портфелю, руб. |
2 312 959 |
2 863 933 |
|
Дисконтированная страховая нетто-премия по портфелю, руб. |
11 551 177 |
10 611 325 |
|
Дисконтированная страховая брутто-премия по портфелю, руб. |
15 401 569 |
14 148 433 |
|
Страховой тариф брутто, доли ед. |
0,1925 |
0,1768 |
Как свидетельствует таблица 4, официальная
методика расчета страховых тарифов не согласуется с результатами имитационного
моделирования, для обеспечения заданной величины надежности страховщика было бы
вполне достаточно более низкого страхового тарифа.
Для наглядности сравнения в рассмотренном
примере ставка доходности принята равной нулю. Если же в таблице 1 учесть
изменение стоимости денег во времени (получение страховщиком доходности от
размещения средств страховых резервов) и задать ставку доходности, равную,
например, 5% годовых, то страховой тариф снизится до 0,1589, то есть более чем
на 10%.
Модель страховых тарифов в официальной
методике базируется на предположении о том, что коллективный убыток по
страховому портфелю распределен по нормальному закону. Однако, как показывает
вычислительный эксперимент [15], если распределение вероятностей коллективного
убытка и близко к нормальному закону, параметры этого распределения
(математическое ожидание и дисперсия) не являются статистически устойчивыми
величинами. Объяснение заключается в следующем. Вывод о нормальности основан на
центральной предельной теореме теории вероятностей, которая, как известно,
справедлива при постоянном числе слагаемых (одинаково распределенных случайных
величин). В случае же коллективного убытка число слагаемых является переменным
и, более того, представляет собой случайную величину, поскольку определяется
количеством наступивших страховых случаев. Соответственно, при каждом новом
испытании сумма коллективного убытка состоит из разного числа слагаемых.
Обычное количество договоров страхования в портфеле, принимаемое для расчета
страховых тарифов, составляет от 100 до 500. При таком количестве договоров
вариация наблюдаемых значений математического ожидания и дисперсии может
оказаться достаточно сильной.
В, пожалуй, наиболее полном руководстве по
общему страхованию [3] перечисленные выше вопросы, к сожалению, не нашли своего
разрешения: наибольшее внимание уделено построению законов распределения на
основе имеющейся статистической информации.
Как следствие, нет возможности говорить о
том, что страховые тарифы в общем страховании являются экономически
обоснованными и соответствуют заданной надежности страховщика.
Аналогично, можно показать, что страховые
резервы по официальной методике [6] не обеспечивают заданной надежности
страховщика. Прежде всего, официальная модель расчета страховых резервов
никаким образом не учитывает такого параметра как величина надежности
страховщика. Кроме того, указанная модель не позволяет учитывать при расчете
резервов обоснованные актуарные предположения о развитии убытков.
Так, в рассматриваемом примере наступление
убытков распределено во времени равномерно в течение каждого года действия
договора, существуют единовременные и периодические расходы, как равномерные,
так и пропорциональные сумме страховых выплат. Если для определенности задать
дату заключения договоров, например, 15.05.2014, смоделировать развитие убытков
и рассчитать суммы резервов по официальной методике, то обнаружится, что в
течение срока действия договора страхования резервы формируются в сумме,
недостаточной для исполнения обязательств страховщика с требуемой надежностью
(рис.). 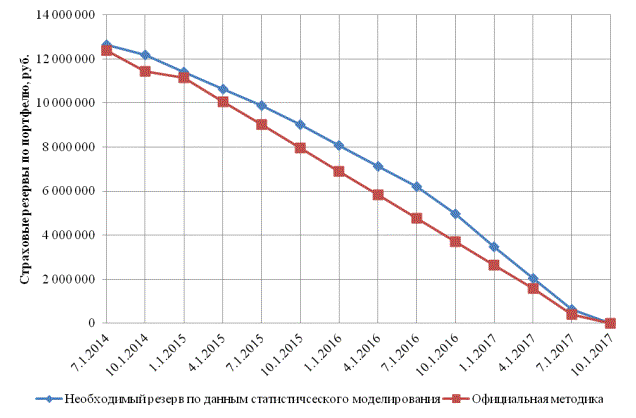
Рис. – Сравнение
страховых резервов по официальной методике с результатами статистического
моделирования
Наблюдаемое на рис. явление противоречит
требованию достаточности страховых резервов, не говоря уже о недостаточно
объяснимой динамике величины страховых резервов в первые три квартала.
Не лучше обстоят дела и с величиной
собственного капитала. Действующие требования предусмотренные [2, 7] заданы в
виде фиксированных сумм и линейных зависимостей от страховой премии и страховых
выплат, не учитывают ни характеристик страхового портфеля, ни требований к
уровню надежности страховщика.
Между тем, собственный капитал выступает в
роли «подушки безопасности» при недостаточности средств страховых резервов.
Соответственно, его величина зависит от расширенной гарантии безопасности
страховщика, которая представляет собой вероятность неразорения с учетом
расходования средств собственного капитала [8, 14].
Для перестрахования (а равно и иных
способов деления риска: франшизы, неполного страхования, сострахования)
отсутствуют проработанные модели, учитывающие соблюдение требований к
финансовой устойчивости страховщика.
Автором предложен [10] обобщенный
актуарный базис, содержащий единый стандартизованный список актуарных
предположений (параметров), который может быть применен как для договоров
страхования жизни, так и для договоров общего страхования. Страховой риск
рассматривается как поток случайных событий, за счет чего может быть учтено
наступление нескольких страховых случаев в течение срока действия страхования,
если это не противоречит существу страхового риска [11].
При этом, как показано в [10], и
страхование жизни, и общее страхование имеют единую природу, отсутствуют
основания считать, что этими двумя отраслями страхования имеются какие-либо
принципиальные различия. И со временем эти различия все больше и больше
стираются: в частности, развивается долгосрочное общее страхование с переменными значениями
вероятности наступления страхового случая, страховой суммы и т.д. В страховании
жизни могут быть выделены краткосрочные полисы: например, страхование жизни на
случай смерти во время туристической поездки, авиаперелета и т. п. Следовательно,
представляется возможным и целесообразным использовать единую актуарную основу
для расчета страховых тарифов (в том числе с учетом деления риска), страховых
резервов, необходимой величины
собственного капитала.
Вариант обобщенного актуарного базиса
представлен в таблице 1.
На основе концепции обобщенного актуарного
базиса разработан единый комплекс моделей оценки и управления финансовой устойчивостью
страховщиков [1, 10-14], который включает в себя модели тарификации, деления
риска, резервирования, определения необходимой величины собственного капитала.
В моделях применяется метод статистических испытаний. Предложенный комплекс
отличается тем, что любая из входящих в него моделей использует исключительно
информацию, содержащуюся в обобщенном актуарном базисе конкретного страхового
риска.
Приведенные выше расчеты в настоящей
статье выполнены с применением данного комплекса моделей.
Для распространенных страховых рисков в
страховании жизни и в общем страховании проведено сравнение [15] страховых
тарифов с тарифами, полученными по
классическим методикам [4, 5]. Сравнение показало, что предложенная модель
тарификации дает результаты, очень близкие к результатам применения
классических методик. Имеются небольшие расхождения при определении страховых
тарифов в общем страховании, но данные расхождения, как было установлено,
обусловлены невыполнением условий центральной предельной теореме теории
вероятностей, которая справедлива при постоянном числе слагаемых (одинаково
распределенных случайных величин).
На основе обобщенного актуарного базиса
также может быть определена необходимая величина собственного капитала,
обеспечивающего финансовую устойчивость страховщика [14]. При этом потребность
в собственном капитале оценивается через предопределенную вероятность
неразорения страховщика с учетом собственного капитала. Тем самым, необходимая
величина собственного капитала страховщика, в отличие от имеющейся методики,
получает строгое научное обоснование.
Таким образом, в результате проведенных
исследований на основе концепции обобщенного актуарного базиса получен комплекс
моделей, позволяющих рассчитывать необходимые параметры страховых операций при
гарантированном соблюдении требований к надежности страховщика. Обобщенный
актуарный базис представляет собой непротиворечивую информационную основу для
таких расчетов. Применение данного комплекса моделей позволило бы сделать более
прозрачными управление и контроль финансовой устойчивости страховщика на основе
системы взаимосвязанных показателей.
Проводится апробация разработанного
комплекса моделей с применением статистического моделирования. В настоящее
время получены результаты, подтверждающие его практическую
применимость для решения задач тарификации и резервирования.
Литература:
1. Бобров
Л.К., Рыжков О.Ю. Расчет страхового тарифа на основе обобщенного актуарного
базиса с учетом деления риска / Л.К. Бобров, О.Ю. Рыжков // Вестник НГУЭУ.
– 2012. – № 1. – С. 188-196.
2. Закон РФ от 27.11.1992 № 4015-1 «Об организации
страхового дела в Российской Федерации» [Электронный
ресурс]: Доступ из справ.-правовой системы «Консультант Плюс».
3. Мак Томас. Математика рискового страхования / Пер.
с нем. – М.: ЗАО «Олимп-Бизнес», 2005. – 432 с.: ил.
4. Методики расчета тарифных ставок по рисковым видам
страхования (утв. распоряжением Росстрахнадзора от 08.07.1993 N 02-03-36)
[Электронный ресурс]: Доступ из справ.-правовой системы «Консультант Плюс».
5. Порядок формирования страховых резервов по
страхованию жизни (Приказ Минфина РФ от 09.04.2009 N 32н) [Электронный ресурс]:
Доступ из справ.-правовой системы «Консультант Плюс».
6. Правила формирования страховых резервов по
страхованию иному, чем страхование жизни (Приказ Минфина РФ от 11.06.2002 №
51н, ред. от 08.02.2012) [Электронный ресурс]: Доступ из справ.-правовой
системы «Консультант Плюс».
7. Приказ Минфина РФ от 02.11.2001 N 90н «Об
утверждении Положения о порядке расчета страховщиками нормативного соотношения
активов и принятых ими страховых обязательств» [Электронный ресурс]: Доступ из
справ.-правовой системы «Консультант Плюс».
8. Приказ Росстрахнадзора от 28.06.1996 № 02-02/18 «О
Методике расчета страховых тарифов по видам страхования, относящимся к
страхованию жизни» [Электронный ресурс]: Доступ из справ.-правовой системы
«Консультант Плюс».
9. Рыжков О.Ю. Моделирование и анализ финансовой
устойчивости страховщиков // Вестник Новосибирского государственного
университета. Серия: Социально-экономические науки. - 2007. - Т. 7. - № 2. - С.
62-73
10. Рыжков О.Ю. Обобщенный актуарный базис страхового
риска // Вестник НГУЭУ. – 2011. – № 2. – С. 166-178.
11. Рыжков О.Ю. Динамический подход к договору
страхования: применение при расчете страховых премий // Вестник НГУЭУ. – 2010.
– № 2. – С. 65-74.
12. Рыжков О.Ю., Бобров Л.К. Тарификация договора
страхования на основе обобщенного актуарного базиса // Вестник СГТУ. – 2013. –
№ 4 (73). – С. 329-335.
13. Рыжков О.Ю., Бобров Л.К. Комплексная автоматизация
деятельности актуария страховой организации // Вестник АГТУ. Серия: Управление,
вычислительная техника и информатика. – 2014. – № 2. – С. 98-108.
14. Рыжков О.Ю. Какой размер собственного капитала
необходим страховой компании? // Идеи и Идеалы. – 2014. – Т.2. - № 3(21). – С.
106-113.
15. Рыжков О.Ю., Бобров Л.К. Оценка точности
численного метода расчета страховых тарифов, основанного на обобщенном
актуарном базисе // Вестник НГУЭУ. – 2014. № 4. – С. 60-80.