Геоэлектриканың кері есебін шешудің Гельфанд – Левитан әдісі

Гельфанд-Левитан әдісінің динамикалық вариантын квазистационарлық жуықтаудағы геоэлектриканың бip өлшeмдi кepi есебін зерттеуге қолданылуын

(1.1)

(1.2)

(1.3)

(1.4) карастырамыз.

Фурье турлендіруінің -параметрі горизонтальды айнымалы бойынша 0-ге тең деп есептейміз. (1.1)-(1.3) аралас есебінің шешімі келесі толқындық теңдеу үшін қойылған

(1.5)

(1.6)

(1.7)

аралас есебінің шешімімен

(1.8)

түрінде байланыста болады, мұндағы

Сондықтан бірінші peттi

интегралдық теңдеуін ға қатысты шеше отырып, біз (1.5)-(1.7)

тура есебінің шешіміне қатысты қосымша (1.9) мәліметті ала аламыз:

(1.9)

Әрине (1.8) интегралдық тендеуін шешудің өзі күрделі мәселе болып табылады, сонда да кейбір жағдайларда бұл бізге бастапқы кepi есептің шешімі туралы манызды мәліметті алуға мүмкіндік береді. Бiз (1.8) интегралдык теңдеуі шешілген деп ұйғарамыз және (1.5) - (1.7), (1.9) кері есебін шешуде Гельфанд-Левитан тәсілінің динамикалық вариантының колданылу схемасын карастырамыз.

Алдагыдай, -ды белгілі оң тұракты деп есептей отырып, жана айнымалы еңгіземіз:

(1.10) және жаңа функциялар еңгізіміз

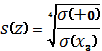
Сонда, егер бойынша қарастырылатын барлық функциялардың жұпжалғасын облысына пайдаланып, функциясы келесі есептің шешімі болатындығына көз жеткізу қиын емес:

(1.12)

(1.13)

Мұндағы

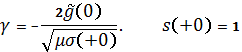
болғандыктан, (1.9) бойынша

(1.14)

болады.

Бізге (1.12)-(1.14) кepi есебін шеше отырып, сосын функциясы бойынша

-ті, олай болса -ті қалпына келтіре алатынымыз анық. (1.12)-(1.14) кepi eceбіне эквивалентті болатын Фpeдгoльмнiң eкiншi peттi сызықтық интегралдық теңдеулерінің

жиынын құрастырамыз. Осы мақсатта кeлeci көмекші есепті еңгіземіз:

(1.15)

(1.16)

операторын түрлендіру үшін Даламбер формуласын қолданамыз, сонда

Ерекшеліктері бойынша жіктеу әдісін пайдаланып, функциясы төмендегідей (1.18) құрылымды болатындығын анықтау қиын емес:

Мундағы функциясы айнымалысы бойынша оң және

болғанда үздіксіз ).

(1.7) бойынша

болғандықтан, (1.19) және (1.14) ескеріп, (1.12) тендеуінің шешімін келесі түрде жазуға

болады:

Мұндагы және функциялары

облысына тақ түрде жалғасқан. Eгep

деп белгілесек және функциясы

болғанда 0-ге тең екенін ескерсек, онда (1.20) тендеуін келесі түрде жазуға болады:

функциясы (1.12), (1.13) есебінің шешімі болғандықтан, сонғы теңдеуден

тендігі шығады.

(1.13), (1.14) шарттарын еркеріп,

нуктесінде функциясы

бірінші peттi узікке ие деп қорытындылаймыз. Олай болса, (1.21) теңдеуін бойынша дифференциалдап, әрбір белгілі

үшін Фредгольмнің екінші peттi тендеуіне келеміз.

(1.22) тендеуін шеше отырып және (1.18) құрылымынан шығатын

теңдігін шеше отырып, біз функциясын

формуласы бойынша аламыз.

Көрсетілген әдістемені толығырак талдау келесі теореманы дәлелдеуге мүмкіндік береді.

Теорема. (1.12)-(1.14) кepi есебінің кесіндісінде бірмәнді шешілуі үшін функциясы келесі шарттарды қанағаттандыруы кажетті және жеткілікті:

1)

2) (1.22) интегралдық теңдеуі кез келген

үшін бірмәнді шешіледі, мұндағы

КОРЫТЫНДЫ

Жұмыста геоэлектриканың бip өлшемді кepi есептерін шешудің әртүрлі сандық әдістері зерттелді. Зерттелу барысында жумыста:

• Максвелл тендеулер жүйесі ушін қойылган көп өлшемді кepi есепті шектелген бip өлшемді кepi есептер жуйесіне келтірудің проекциялық әдісі көрсетіледі;

• жағдайында Максвелл теңдеулер жуйесі yшін қойылған бip өлшемді кері есепті шешудің сандық алгоритмі көрсетілді;

• Гельфанд-Левитан әдісінің динамикалық вариантына сәйкес Максвелл теңдеулер жуйесі үшін қойылған бір өлшемді кepi есепке эквивалентті сызыкты Фредгольмнің екінші текті интегралдық теңдеулер жуйесі алынды.

Жұмыс нәтижелерін практикалық маңызы зор геофизиканың көптеген кepi есептерін шешуде және оқу процесінде пайдалануға болады.

Әдебиеттер:

1. Елубаев С.Е., Ділман Т. Гиперболалық және параболалық теңдеулер үшін кейбір кері есептер.-Алматы, 1992. – 183б.

2. Баканов Г.Б. Методы решения конечно-разностных обратных задач теории распространения волн. – Кызылорда, 2001.-128с.

3. Тихонов А.Н., Арсенин В.Я. Методы решения некорректных задач.-М: Наука, 1974. -224с.