А. А. Кудь, А. Б. Щукин, А. В. Макаричев, к.ф.-м.н., доц.

Национальный аэрокосмический университет «ХАИ»

Харьковский национальный автомобильно-дорожный университет

Московский государственный университет им. М.В. Ломоносова

ГАММА ИДЕНТИФИКАЦИЯ АЛЬТЕРНИРУЮЩЕГО ПРОЦЕССА

При использовании новой техники возникают альтернирующие процессы. Моменты их идентификации представляют собой поток однородных событий [1]. В некоторый момент времени возникает скачок вверх альтернирующего процесса, продолжительность пребывания которого в этом состоянии (продолжительность сигнала) есть неотрицательная случайная величина с функцией распределения . Нас интересует вероятностное распределение времени от начала сигнала до момента его обнаружения при условии, что он обнаружен.

Предположим, что поток моментов идентификации альтернирующего процесса является стационарным рекуррентным и время между соседними моментами идентификации имеет функцию распределения

,

и плотность распределения

, .

Нетрудно видеть, что вероятность того, что возникший сигнал не будет обнаружен, равна

,

А вероятность обнаружения возникшего сигнала определяется по формуле

,

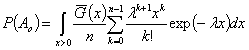где .

Функция распределения случайной величины - времени от начала сигнала до момента его обнаружения при условии, что сигнал будет обнаружен, равна

, .

Условное математическое ожидание времени от момента начала сигнала до момента его обнаружения при условии, что он обнаружен, равно

.

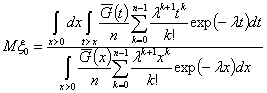Моменты случайной величины - условного времени от момента начала сигнала до момента его обнаружения при условии, что он обнаружен, найдем в виде

, .

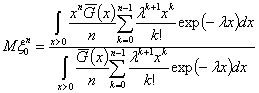А её дисперсия равна

.

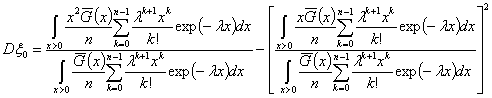Пусть - функция распределения времени между соседними сигналами альтернирующего процесса. Обозначим случайное время от момента окончания сигнала до момента очередной гамма идентификации при условии, что до этого момента новый сигнал не начался. Функция распределения случайной величины имеет вид

, .

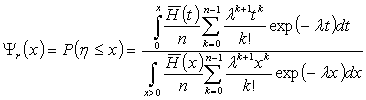Условное математическое ожидание времени от момента окончания сигнала до момента очередной гамма идентификации при условии, что до этого момента новый сигнал не начался, равно

.

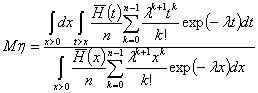Моменты случайной величины времени от момента окончания сигнала до момента очередной гамма идентификации при условии, что до этого момента новый сигнал не начался, имеют вид

,

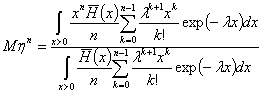А дисперсия времени от момента окончания сигнала до момента очередной гамма идентификации при условии, что до этого момента новый сигнал не начался равна

.

Вероятность же того, что за время после окончания сигнала до момента очередной гамма идентификации начнется очередной сигнал, равна

.

Литература.

1. B. V. GNEDENKO AND I. N. KOVALENKO, Introduction to Queueing Theory, Program for Scientific Translations, Jerusalem, 1968.

2. Соловьев А. Д. Асимптотическое поведение момента наступления

редкого события в регенерирующем процессе. Известия АН СССР.

Техническая кибернетика, 1971, № 6, с. 79-89.

3. Вопросы математической теории надежности/Е. Ю. Барзилович, Ю. К.

Беляев, В. А. Каштанов, И. Н. Коваленко, А. Д. Соловьев, И. А. Ушаков;

Под ред. Б. В. Гнеденко.- М.: Радио и связь, 1983.- 376 с., ил.

4. Ширяев А.Н. Вероятность, М.: Наука, 1980, 576 c.