Д.ф.-м.н. Срумова Ф.В.

Таджикский национальный университет

 

ОБ АБСОЛЮТНОЙ И РАВНОМЕРНОЙ СХОДИМОСТИ ОБОБЩЕННОГО ИНТЕГРАЛА ФУРЬЕ

 

         Доказана абсолютная и равномерная сходимость обобщенного интеграла Фурье.

         Ключевые слова: обобщенный интеграл Фурье.

 

Пусть  -мерное евклидово пространство,  -оператор Лапласа,  ограниченная замкнутая область в . Мы предположим, что граница области   принадлежит классу Ляпунова. Пусть -расширение оператора  , отвечающее краевым условиям одного из следующих типов:

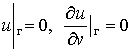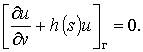                            или                          (1)

         Определение. Функция   называется собственной функцией непрерывного спектра оператора , если она удовлетворяет уравнению

граничным условиям (1)  и представима в виде

где   удовлетворяет условиям излучения

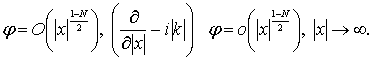
         Как известно  [1,2], для  любой функции   справедливы равенства

                    где                  (2)

(Интегралы в (2) понимаются в смысле сходимости в среднем). Назовем первый из интегралов в (2) обобщенным интегралом Фурье.

         Теорема. Если , где  -любое число, удовлет-воряющее неравенству  , и равна нулю в пограничной полосе, то обобщенный интеграл Фурье сходится абсолютно и равномерно для  .

         Доказательство теоремы опирается на следующие леммы.

         Лемма 1. Если   где  , и обращается в нуль в пограничной полосе, то

                                           .                                    (3)

         Доказательство. Прежде всего, преобразуем интеграл (3)

          

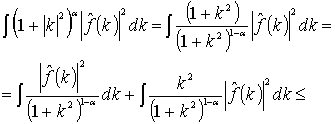
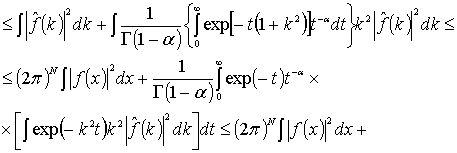
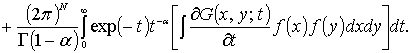                                       (4)

Затем, пользуясь равенством

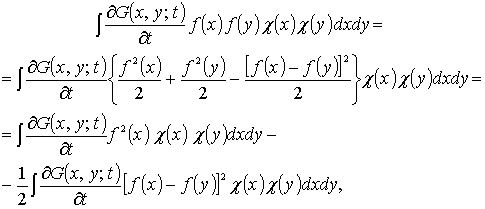
где  -бесконечно гладкая функция, равная единице на носителе   и нулю в погранполосе области , получаем

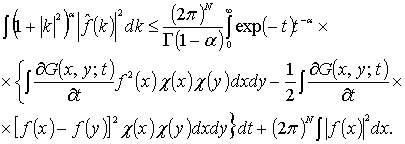                                     (5)

Оценим первый интеграл, стоящий в правой части (5),

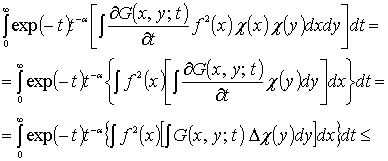
                           (6)

Далее, из справедливости оценки

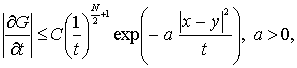
вытекает, что

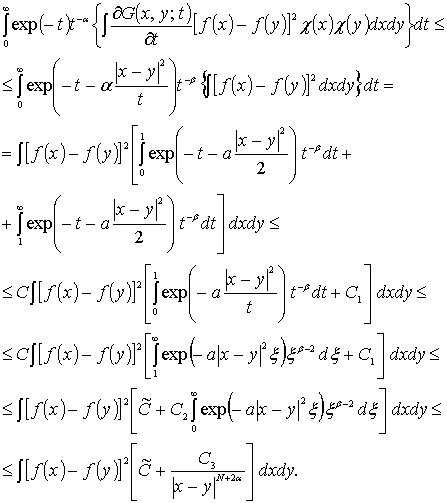                                 (7)

Сопоставляя (5), (6), (7), получим  .

         Лемма 2. Если  , где  , и обращается в нуль в пограничной полосе, то

                                             .                                (8)

         Доказательство. Положим  , где  , и преобразуем интеграл (8)

         

      

        

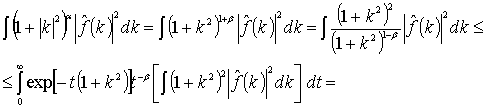
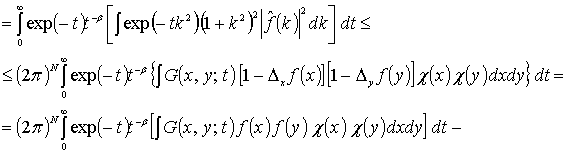
                           (9)

Используя следующее равенство

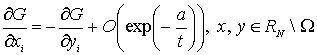                           ,                            (10)

оценим второй интеграл, стоящий в правой части (9),

                      

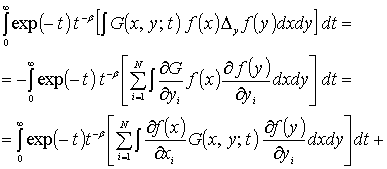
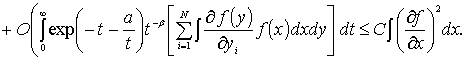                        (11)

Далее отметим, что справедлива следующая оценка:

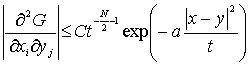                                                                       (12)

и  будем оценивать третий интеграл, стоящий в правой части (9). Нетрудно заметить, что

                   

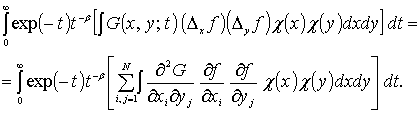
Справедливо равенство

              

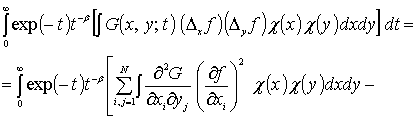
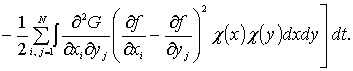                                   (13)

Оценим первый интеграл правой части (13)

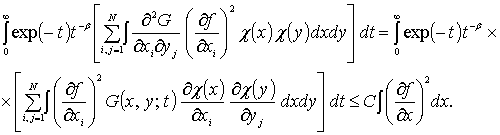                    (14)

Согласно (12), второй интеграл правой части (13) имеет вид

 

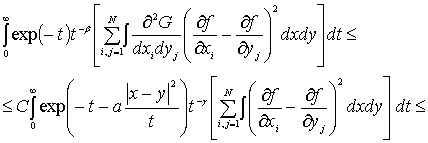
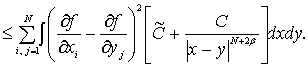                                                                     (15)            

И, наконец, оценим первый интеграл правой части (9). Имеем

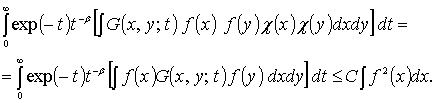                                (16)

Из (9), (11), (14), (15) и (16) следует, что

         Лемма 3. Если   и , то интеграл 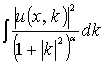  сходится равномерно относительно .

         Доказательство. Пользуясь соотношением

и оценкой функции Грина при  , получим

              

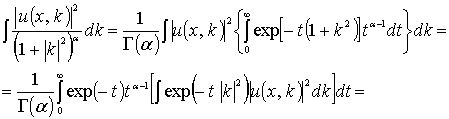
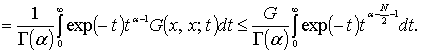                                  (17)

Последний интеграл в (17) сходится равномерно относительно  при . Лемма 3 доказана.

         Перейдем теперь к доказательству теоремы. Применяя неравенство Коши - Буняковского, получаем

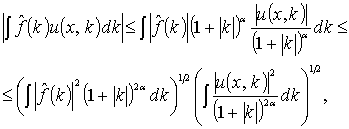
где первый из интегралов сходится в силу лемм 1,  2, а второй-леммы 3. Теорема доказана.

         Замечание. Существует функция , где 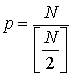  такая, что не может быть речи об абсолютной сходимости обобщенного интеграла Фурье при , поскольку эта функция имеет особенность типа  .

        

 

Литература

 

1.     I k e b e  T. - Archive for Rational Mech. and Anal., 1960, т.5, с.1-34.

2.     I k e b e  T. - Jap. J. Math., 1967, т.36, с.33-55.