Конференция «Современный научный потенциал - 2015»

Секция «Математика»

к.ф.м.н. Ивлиев Ю.А.

Международная Академия Информатизации, Россия

yuri.ivliev@gmail.com

ВЕЛИКАЯ ТЕОРЕМА ФЕРМА КАК ОБРАТНАЯ ЗАДАЧА МАТЕМАТИЧЕСКОЙ ПСИХОЛОГИИ.

Доклад посвящен следующим вопросам: 1. Почему Великая теорема Ферма стала изгоем официальной математики ? 2. Как математическая психология раскрывает новый смысл теоремы Ферма в виде обратной задачи математического моделирования ? 3. Спасет ли будущая научная парадигма, предвосхищенная Великой теоремой Ферма, человечество от лжи и самоуничтожения ?

Ключевые слова: Великая теорема Ферма, гипотеза Биля, математические структуры объективного мира.

1.Введение. Почему Великая теорема Ферма стала изгоем официальной математики ?

Современные исследования Великой теоремы Ферма (далее: ВТФ) как самой загадочной математической проблемы, относящейся к теории чисел, натолкнулись на железобетонную стену тотального их неприятия со стороны корпоративной (читай: официальной) математики [1;2]. Автор доклада считает, что такое положение вещей обусловлено двумя главными причинами. Первая причина заключается в общем культурном невежестве основной массы профессиональных математиков, зациклившихся на своих узкопрофессиональных интересах и презрительно относящихся к любым математическим изыскам непрофессионалов [3]. Такое их высокомерие играет с ними злую шутку: после того, как они скармливают новичкам фальшивые определения математических объектов, они и сами подпадают под гипноз своих же собственных иллюзий. Но главное зло заключается в том, что эти иллюзии завладевают тотальным корпоративным мышлением, заставляя математическое сообщество жестко консолидироваться под страхом неминуемого отлучения нонконформистов от математической церкви. В случае с ВТФ, это иллюзия ее корпоративного доказательства, которое никто не может воспроизвести и которое, естественно, никогда не может быть разъяснено хотя бы на уровне вузовской математики.

Вторая причина заключается в том, что широкие массы энтузиастов ВТФ, завороженные простотой ее формулировки и генетической связью с теоремой Пифагора, как сердцевиной древней сакральной математики, всегда чувствовали на уровне своих высших ощущений, что в ВТФ заложена математическая истина, вполне доступная проницательным исследователям. Только вот отточить свою проницательность до необходимой степени остроты и чистоты многим оказалось не под силу из-за незнания чистой (фундаментальной) математики, оберегаемой от непосвященных фальшивыми рецензентами и некомпетентными популяризаторами науки. Таким образом, ВТФ оказалась запертой в золотой клетке, ключик от которой так и не был найден официальной наукой, несмотря на все усилия корпоративных математиков убедить культурное население планеты в обратном.

2.Математическая психология раскрывает новый смысл теоремы Ферма в виде обратной задачи математического моделирования.

Между тем автор доклада давно нашел способ восстановить утраченное (не записанное Пьером Ферма) доказательство ВТФ [4]. С этой целью пришлось обратиться к психологии научного творчества и, в частности, к математической психологии, решающей математическими методами психологические задачи. К последним можно отнести эвристический поиск математических объектов с наперед заданными свойствами. Подобными задачами занимаются также такие разделы психологии, как психология творческого мышления и психология математики, фактически являющаяся обратной стороной (изнанкой) математической психологии.

Итак, вначале надо было сформулировать проблему, чтобы приступить затем к ее исследованию. Проблема ВТФ заключается в том, что для степеней целых чисел с показателем n > 2 невозможно записать равенство, аналогичное равенству Пифагора для степеней целых чисел при n = 2 [4]. И вот здесь, после осознания этой проблемы, Ферма делает первый творческий шаг, а именно, допускает, что уравнение для высших степеней целых чисел, аналогичное уравнению Пифагора, существует (в современной математике такое предположение относят к методу доказательства от противного). Чтобы построить уравнение Ферма для целых чисел, следует, по-видимому, применить метод построения уравнения Пифагора. Последнее легко получается из геометрической теоремы Евклида для средних пропорциональных.

Но и уравнение Ферма также может быть получено последовательным применением теоремы Евклида, только с той разницей, что одно из слагаемых в равенстве Ферма само оказывается равенством Ферма, но в меньших целых числах, и требует применения того же метода в бесконечной цепочке все меньших и меньших равенств Ферма. На этом шаге Ферма завершает демонстрацию своего метода, назвав его заключительный этап бесконечным спуском, который собственно и доказывает ВТФ вследствие того математического факта, что целые степени целых чисел не могут быть меньше единицы.

Однако при построении уравнения Ферма с помощью теоремы Евклида существует один тонкий математический момент – это установление тождества разбиений какой-либо высшей степени целого числа на два аналогичных слагаемых разбиениям на три слагаемых в цепочке преобразований, генерируемых теоремой Евклида. Между разбиениями на два и на три слагаемых существует взаимнооднозначное соответствие, т.е., другими словами, между гипотетическим равенством Ферма и построенным разбиением на три слагаемых существует изоморфизм (сохранение структуры равенства Ферма). Обратное приведение полученных разбиений к виду уравнения Ферма и составляет обратную задачу математического моделирования искомого равенства для высших степеней целых чисел. Обратные задачи математического моделирования давно изучаются в различных областях науки (математической физике, математической биологии и т.д.), но только Ферма смог открыть первую обратную задачу в математической психологии, что и вызвало у него реакцию восторженного изумления, когда он записывал формулировку своей теоремы на полях «Арифметики» Диофанта.

3.Заключение. Будущая научная парадигма, предвосхищенная Великой теоремой Ферма, спасет человечество от лжи и самоуничтожения.

В докладах [3;5], рассматривающих гипотезу Биля как обобщенную ВТФ, автор попытался хотя бы вкратце обрисовать значение ВТФ для будущей науки. В частности, при исследовании ВТФ было отмечено, что в основе объективно наблюдаемого мира лежат математические структуры, управляющие всем многообразием его свойств. Эти структуры являются истиной в последней инстанции, за которой нет ничего другого и от которой надо отталкиваться, чтобы идти по верному пути прогресса. Однако, если постоянно не сверять свои действия (исследования, теории, модели) с этой глубинной математической реальностью, то существует серьезная опасность, даже в области математики, свернуть с истинного пути и устремиться в иллюзорные дали спекулятивных теорий. Значит, в изучении любых явлений природы и человеческого социума надо полагаться, прежде всего, на истинность математического доказательства, а не на внешние атрибуты опытных данных или результатов экспериментов, предпринятых для проверки гипотетических моделей. Только так, по-видимому, можно будет избавиться от присущей человеческой природе склонности ко лжи и самообману.

Древние люди, по-видимому, хорошо умели чувствовать глубинную основу бытия и могли в своих сакральных образах и символах точно выразить то, что в современных фундаментальных науках дается с таким колоссальным трудом и постоянными издержками и ошибками [6;7]. Конечно, они не оперировали современными математическими понятиями, которые являются продуктом своей эпохи, но с помощью доступных им средств могли наглядно представлять действующие принципы бытия без разрушительных последствий от их применения. Одним из самых наглядных и эффективных древних символов является символ Тай Чи («китайская монада»), заключающий в себе все известные современной науке фундаментальные принципы, а также не известные еще системные принципы, увязывающие основные научные категории, такие, как пространство, время, движение, энергия и другие, в единую систему бытия. Так вот главной заслугой ВТФ перед будущей наукой явилось открытие математической структуры китайской монады, совпадающей со структурой ВТФ. На рис.1, взятом из работ [5;6], изображена эта структура в действии (обозначения на рис.1 объяснены в работах [5;6]).

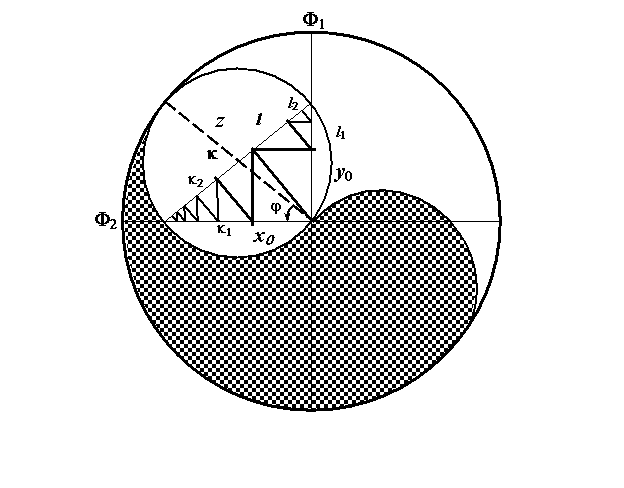
Рис. 1

Завершая свой доклад о смысле и значении ВТФ, автор видит свое участие в дальнейшей работе по изучению ее структуры в виде масштабного научно-исследовательского проекта, имеющего своей целью создание новой научной парадигмы одухотворенного человечества, избавленного с ее помощью от химер лжи и самообмана.

Литература.

1. Руди Л.В. Неопубликованные рукописи (из архива Ю.А.Ивлиева).

2. URL: http://yuri-andreevich-ivliev.narod.ru/

3. Ивлиев Ю. А. Преступная математика (как корпоративная наука блокирует появление новой научной парадигмы) – Materials of the XI International Scientific and Practical Conference “Areas of Scientific Thought – 2014/2015”, vol. 9, Sheffield, December 30, 2014 – January 7, 2015, pp. 46-52.

4. Ивлиев Ю. А. Реконструкция нативного доказательства Великой теоремы Ферма – Объединенный научный журнал 2006 № 7, 3-9.

5. Ivliev Y. A. Beal’s Conjecture as global break-through in natural sciences –Materials of the I International Scientific Conference “Global Science and Innovation”, vol. II, Chicago, December 17-18, 2013, pp. 345-349.

6. Ivliev Yuri Sacred mathematics of ancient symbols: on the example of the Chinese monad geometry and arithmetical geometry of the Fermat’s Last Theorem – GISAP History and Philosophy 2014 No. 2 pp.16-18.

7. Ivliev Yuri Fermat’s Last Theorem in the context of the modern natural-science knowledge – GISAP 2014 No. 2 pp.44-46.