Burakovski V

Burakovski V.V.

Gomel State University, Belarus

Nonsymmetric Dual-Ring Token-Passing Local Area Network

Abstract: A nonsymmetric dual-ring token-passing local area network with N stations in which each station has a single buffer is studied. The message arrival streams at each station are assumed to be independent Poisson processes with arrival rate λ_i for the i-th station, 1 ≤ i ≤ N. The stationary probabilities of considered local area network and main characteristics were obtained.

Introduction. Token-passing is one of the most effective schemes to eliminate contention among stations in a ring data-communication network. It involves passing the token, which is a special bit pattern, from one station to another. The station that holds the token has control over the medium for a predetermined amount of time, which is referred as the token-holding time in the IEEE 802.5 standard [2]. Token-passing on a ring configuration ensures that all stations tied to the ring have an opportunity to send messages. In a token ring network the token circulates cyclicly among the stations so that arriving messages at stations can be transmitted in a round fashion.

In this paper we propose a “dual-ring” architecture with token passing protocol. The proposed approach is based on the idea that there are two rings and two tokens circulate in network [1]. Ring 1 is referred as the forward channel. The token travelling along the forward channel is referred as the forward token and is denoted as T_f.

The second ring is referred as the reverse channel. The token in this ring is the reverse token and is denoted as T_r. The forward and the reverse token move in opposite directions. In other words, the network stations form a doubly linked list, which not only knows its “next” station but also is aware of its previous station.We assume that T_f and T_r arrive and leave the stations at the same moments.

Analytical model. A nonsymmetric dual-ring token-passing local area network with N stations is considered. Each station has a single buffer. The walk time for the forward or reverse token to move from one station to the next one is assumed to be a constant equal to δ. The service time for any station is a. During this time the station serves message if it is in buffer or waits for the moment of departure if buffer is empty. The message arrival streams at each station are assumed to be independent Poisson processes with arrival rate λ_i for the i-th station,1 ≤ i ≤ N.

We consider the ordinary service discipline, which assumes that the station transmits message when the token arrives, but none of those messages that arrive after the token [4]. So no more than one message can be transmitted from the station during T_f or T_r is at this station.

Let us denote by (i,j,k₁,…k_N) the state of the dual-ring local area network, where i – is the number of the station where T_f arrives and j – is the number of the station where T_rarrives, k_m – is the number of customers at the m-th station, 1 ≤ m ≤ N, at the moment when T_f and T_r arrive at correspondent stations, k_m{0,1}. The stationary probabilities of these states are P (i,j,k₁,…k_N).

1. The stationary probabilities. The behavior of our dual-ring network at the moments when T_f and T_r arrive at the stations we can describe with the help of periodical Markov chain. Let us denote by A_ij, 1 ≤i, j ≤ N, the matrix of the transition probabilities, where i and j are the numbers of the stations where T_f and T_r arrive correspondently. It is evident that the numbers of the next stations where T_f and T_r arrive from the stations i and j are i+1 and j-1. Let us denote by P(i,j) the stationary probabilities vectors, 1 ≤i, j ≤ N.

The steady-state probabilities of considered queuing system are the solution of the following matrix-vector system:

;

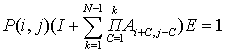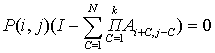where 1≤ i,j≤N, E is vector of 2^N units, I –is (^2N 2^N) matrix а units, A_ij- (2^N2^N) matrix of the transition probabilities. These probabilities are

where 0≤k,r≤2^N-1, I_{B}-is the indicator of set B, ,

α_с–are the coefficients of the state (i, j, α₁,…, α_N), β_c–are the coefficients of the state (i+1, j-1, β₁,…, β_N).

2. The main characteristics. The main characteristics of the considered network are [3], [5], [6], [7]:

1) the probability that there are no messages in the network(the network is empty);

2) the probability that there are messages at each station;

3) the load coefficient for the i-th station;

4) the load coefficient of the network;

5) the mean service time at each station;

6) the mean return time for the T_f and T_r;

7) the mean number of lost customers in the network;

8) the mean number of busy stations;

9) the mean delay time at the station.

The definition of these characteristics is based on the steady – state probabilities (1). We have obtained the dependence for the main characteristics of the network on messages arrival rates.

3. Conclusions. The present paper has presented the mathematic model of nonsymmetric dual – ring token – passing local area network with single buffer stations. The methodology used is based on the cyclic Markovian processes [4]. It is interesting to investigate the LAN with different service disciplines (k-limited, gated, Bernoulli) and finite capacity buffers at each station. The processes in such networks are very similar to the cell telephone stations widely used now. The description of the symmetric dual – ring LAN is also very actual because of its complexity.

References

1. Wu Jean–Lien C., Wu Jingshown, Huang Tien-Yu. A reliable token – passing bus LAN with reservation / Wu Jean–Lien C., Wu Jingshown, Huang Tien-Yu // IEEE Infocom`89 Conf. Comput. Commun. – 1989. – Vol 1. – Р. 1–8.

2. ANSI/IEEE 802.5 Standard – 1985. Token-passing ring access method and physical layer specification. – IEEE Press, 1985. – 89 p.

3. Bux, W. Performance issues in local – area networks / W. Bux // IBM Systems Journal. – 1984. – Vol. 23, No 4. – Р. 351–374.

4. Takagi, H. Analysis of polling systems / H. Takagi. – Cambridge, M.A. : MIT Press, 1989. – 198 p.

5. Бураковский, В.В. Маркерная кольцевая локальная сеть с конечными буферами и ординарным обслуживанием сообщений / В.В. Бураковский // Аэрокосмическое приборостроение России. Сер. 2, Авионика. – 1998. – Выпуск 1, Санкт-Петербург, НААП, с. 63–67.

6. Бураковский, В.В., Медведев, Г.А. Кольцевая локальная сеть с протоколом маркерного доступа / В.В. Бураковский, Г.А. Медведев // Техника средств связи. Сер. Системы связи. – 1990. – Вып. 7. – С. 9–16.

7. Бураковский, В.В. Исследование кольцевых маркерных локальных вычислительных сетей при помощи циклических марковских процессов / В.В. Бураковский. – Гомель, 1997. – 15 с. (Препринт / Гомельский государственный университет им. Ф. Скорины; № 31).