ОПРЕДЕЛЕНИЕ
МАКСИМАЛЬНЫХ ВЕЛИЧИН ИЗГИБА ГРАНИЦЫ ПОЛОСОВОГО ДОМЕНА ПО ПАРАМЕТРАМ МАГНИТНОЙ
ЭЛЛИПТИЧЕСКОЙ НЕОДНОРОДНОСТИ
М.Л. Акимов, А.П. Буйда, П.А. Поляков, Н.Н. Усманов
Московский государственный университет им. М. В .Ломоносова, Физический факультет, Россия
Развитие приборов и устройств, в которых используются магнитные пленки в качестве магнитных носителей информации, стимулировало экспериментальные и теоретические исследования магнитных структур в различных материалах.
На реализацию доменной структуры в равновесных состояниях в реальных условиях оказывает влияние наличие в ферромагнетике неоднородностей и дефектов магнитного и немагнитного происхождения: примеси, пустоты, дефекты атомной структуры, форма поверхности образца и т. д. Точный аналитический расчет доменной структуры при наличии таких дефектов представляет собой сложную проблему [1].
В работах [2-4] были получены смешанные доменные структуры, состоящие из полосовой доменной структуры и магнитной неоднородности в форме цилиндра и эллипса. В данной работе были получены теоретические зависимости величины максимального изгиба границы полосового домена от параметров магнитной неоднородности. Также экспериментально были получены полосовые доменные структуры при наличие в них эллиптических магнитных доменов. Проведено сравнение экспериментальных значений максимальных изгибов доменных границ полосового домена в результате воздействия поля рассеяния эллиптического магнитного домена с полученными теоретическими результатами.
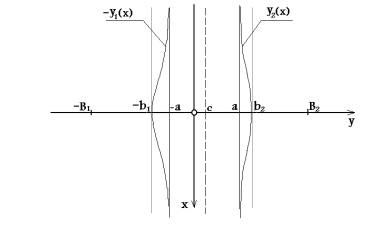
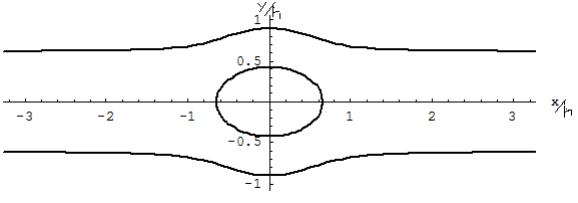
Рис. 1.
Рассмотрим единичный изолированный полосовой домен (Рис. 1) при
наличии внутри него магнитного домена в форме эллиптического цилиндра (где ![]() - большая,
- большая, ![]() - малая
полуось эллипса вытянутого вдоль полосового домена, с – параметр несимметричности). Начало системы координат помещено в
центр эллиптической области (например: ЦМД, эллиптическая магнитная
неоднородность). На Рис. 1 изображен изолированный полосовой домен ширины w=2a, расположенный вдоль
координатной оси x в бесконечной пленке толщины h. Координатная ось z направлена перпендикулярно
плоскости пленки, а ось y - перпендикулярно доменной стенке.
- малая
полуось эллипса вытянутого вдоль полосового домена, с – параметр несимметричности). Начало системы координат помещено в
центр эллиптической области (например: ЦМД, эллиптическая магнитная
неоднородность). На Рис. 1 изображен изолированный полосовой домен ширины w=2a, расположенный вдоль
координатной оси x в бесконечной пленке толщины h. Координатная ось z направлена перпендикулярно
плоскости пленки, а ось y - перпендикулярно доменной стенке.
Воздействие неоднородности исказит формы доменных
границ и приведет к зависимости их от координаты x. Пусть функции ![]() и
и ![]() определяют
изгибы левой и правой доменных стенок в результате влияния несимметричного
цилиндрического домена эллиптической формы. Были получены аналитические формулы
для расчета искажений форм доменных границ,
обусловленных воздействием несимметричного цилиндрического домена эллиптической
формы, которые имеют следующий вид:
определяют
изгибы левой и правой доменных стенок в результате влияния несимметричного
цилиндрического домена эллиптической формы. Были получены аналитические формулы
для расчета искажений форм доменных границ,
обусловленных воздействием несимметричного цилиндрического домена эллиптической
формы, которые имеют следующий вид:
 ,
,
 , (1)
, (1)
где


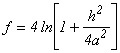 ,
,
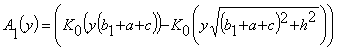
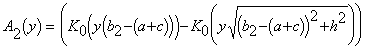 ,
,
 ,
,
 , ,
, ,
![]() и
и ![]() - максимальные
значения модуля функций
- максимальные
значения модуля функций ![]() и
и ![]() , описывающих формы искажений доменных границ
полосового домена вследствие магнитостатического поля рассеяния несимметричного
цилиндрического домена эллиптической формы, h – толщина магнитной плёнки. При с = 0 (параметр несимметричности)
формулы (1) преобразуются в симметричный случай, когда магнитная неоднородность
расположена в центре изолированного полосового домена.
, описывающих формы искажений доменных границ
полосового домена вследствие магнитостатического поля рассеяния несимметричного
цилиндрического домена эллиптической формы, h – толщина магнитной плёнки. При с = 0 (параметр несимметричности)
формулы (1) преобразуются в симметричный случай, когда магнитная неоднородность
расположена в центре изолированного полосового домена.
С помощью
формул (1) определена форма полосового домена при наличии внутри него
магнитного домена в форме эллипса

и построены теоретические зависимости величины максимального
изгиба границы полосового домена от параметров эллиптической магнитной
неоднородности.
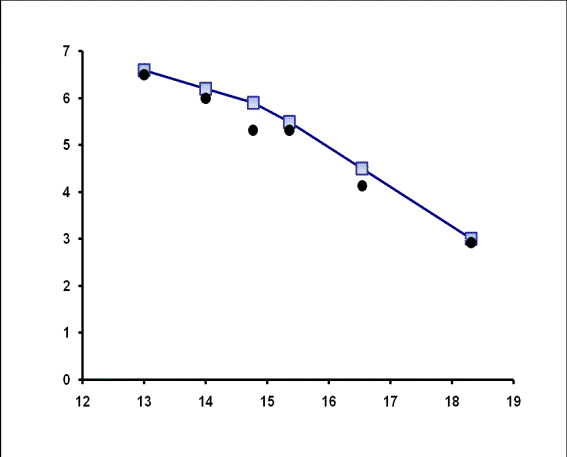
На рис. 2 черными кружками отмечены значения
максимального изгиба доменной стенки,
полученного из эксперимента, для значения большой оси эллипса 23мкм. На оси
абсцисс отложена ширина полосового
домена, внутри которого локализован эллиптический домен. Квадратиками показаны расчетные
значения величины изгиба доменной стенки.
![]()
![]()
Из рисунка видно , что экспериментальные значения максимального изгиба границы
полосового домена незначительно
отличаются от теоретических значений, рассчитанных
по формуле (1). Проведенные эксперименты показывают, что рассмотренная
теоретическая модель пригодна для описания
изменения формы доменной стенки сложной доменной структуры с
эллиптической неоднородностью.
Литература
1.
Ландау Л. Д.,
Лифшиц Е. М. Электродинамика сплошных сред. М.: Наука. 1992, 664 с.
2.
М. Л. Акимов,
П. А. Поляков, Н. Н. Усманов. ЖЭТФ, 121 (2002) с. 347-353.
3. M. L.
Akimov, P. A. Polyakov, Y. V. Starokurov, N. N. Usmanov,
Y. N. Fedyunin. Physica B 405 (2010) 2376–2379.
4.
М. Л. Акимов,
П. А. Поляков. Вест. Моск. ун-та, сер. 3, физ. астр., 2004, № 2,
с.47-50.