О МОДЕЛЯХ НЕПОЛНОГО КОНТАКТА

ДВУХСЛОЙНЫХ УПРУГИХ ПОЛОС ИЗ ОРТОТРОПНЫХ СЛОЕВ

ГЕВОРКЯН Р.С.

Асимптотический метод решения неклассических краевый задач теории упругости был предложен и впервые применен в [1]. Эффективность метода позволила решить множество статических и динамических задач для анизотропных полос (балок), пластин и оболочек  [2-9]. Эта эффективность заключается в том, что в отличие от асимптотического метода [10,11], предложенным подходом [1-9] выводятся рекуррентные  расчетные формулы для компонент тензора напряжений и вектора перемещения упругого тонкого тела, которые позволяют вычислить их значения с любой асимптотической точностью. И, поскольку после каждого шага итерации эти расчетные рекуррентные формулы  подразумевают одно интегрирование по поперечной координате и одно дифференцирование по продольным координатам, они  приводят к замкнутому математическому решению краевой задачи для анизотропных полос и пластин бесконечных  продольных размеров после конечного числа шагов, когда заданные в уравнениях и в граничных условиях функции являются полиномами продольных координат.

 Учитывая  это, в работе выводятся математически точные решения ортотропной двухслойной полосы с кинематиескими граничными условиями при различных наиболее часто встречающихся  моделей   неполного контакта между слоями. Проводится анализ существующих моделей и предлагается  обобщенные модели упругого контакта слоев. 

1.     Постановка краевой задачи и общий интеграл асимптотического

решения внутренней за­дачи. Имеем узкую прямоугольную двухслойную ортотропную полосу в двумерной декартовой  системе координат занимающую область  (фиг.)

На продольных краях полосы заданы компоненты вектора перемещения

                                     (1.1)

Требуется определить напряженно-деформированное состояние двухслойной полосы, если на линии (поверхности) раздела слоев задана одна из комбинаций условий  неполного контакта слоев [12,13]:

а).     по аналогии гипотез Винклера – Фусса

        

                                                                  (1.2)

              

(Эта модель предполагает образование плотного слоя толщины  в зоне контакта шероховатых поверхностей, который подвергается сдвигу по длине поверхности контакта на величину , где  – перемещения точек верхнего и нижнего (краев) берегов воображаемого уплотненного слоя контакта шероховатостей и  – соответственно его касательное напряжение и модуль сдвига).

б). по аналогии закона сухого трения Кулона

                                                                 (1.3)

                        

                                                                      

                                                                  

    

      

                                                       

                

  ///////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////

         

                                                    Фиг.

                      

 

В  формулах (1.2),(1.3), выражающих модели неполной связи слоев, величина   должна быть задана для  корректности поставленных задач (например, при полном котакте слоев ), однако в сформулированных задачах она величина неизвестная, поскольку дана величина определяющая модель  неполной связи слоев , и поэтому не нарушаеся корректность поставленных краевых задач. Исходя из этого значения  зависят от модели неполного контакта слоев.                 

Для решения поставленной задачи приведем уравнения равновесия и соотношения упругости , в общем случае, плоской задачи ортотропного упругого тела в плоскости

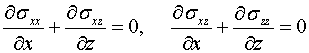                                                          (1.4)

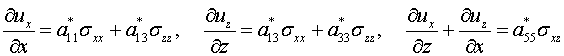
При плоском напряженном состоянии   получают вид

(1.5)

(физико-механические коэффициенты ортотропного упругого тела обозначены , а для изотропного тела они приведены в скобках).

А при плоском деформационном состоянии   должны иметь вид

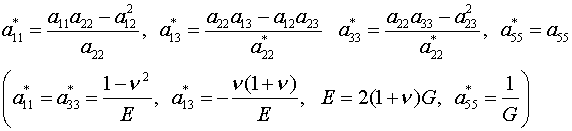(1.6)                                             

В уравнениях и соотношениях (1.4) переходим к безразмерным координатам и перемещениям по формулам

                     (1.7)    

и получаем

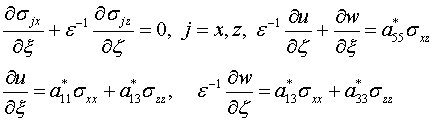                             (1.8)                                                      

 Система уравнений и соотношений (1.8) сингулярно возмущена геометрическим малым параметром . Cледовательно ее асимптотическое решение складывается из двух типов решений [3–4,10, 14,15]. Первое – решение внутренней задачи , которое удовлетворяет  граничным условиям, заданным на продольных краях полосы и доминирует внутри области, занимаемой полосой. Второе решение, –является решением задачи пограничного слоя, которое  на лицевых поверхностях тонкого тела удовлетворяет соответствующим однородным (нулевым) условиям  и в сумме с решением внутренней задачи удовлетворяет граничным условиям, заданным на боковых краях  (торцах) полосы. Как правило оно доминирует вблизи торцов и экспоненциально убывает по направлению внутренней нормали к поверхности торцов.

         Решение внутренней задачи ищется в виде асимптотического разложения

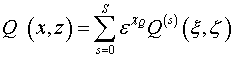                                               (1.9)                                                                                                                  

где – любая из неизвестных компонент  вектора перемещения  и тензора напряжений ,  –асимптотический  порядок соответствующей величины, который  – для всех перемещений и  – для всех напряжений.

Подставив (1.9) в сустему (1.8) после  некоторых несложных преобразований, получим общий интеграл поставленных краевых задач в виде следующующей системы рекуррентных формул

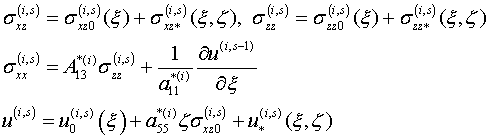
                                                    (1.10)            

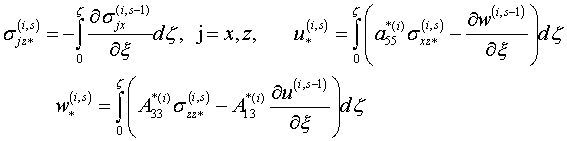
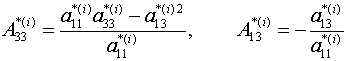
Удовлетворив граничным условиям  (1.1) и общим условиям контакта слоев из (1.2) и (1.3)  получаем

 

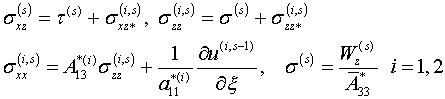
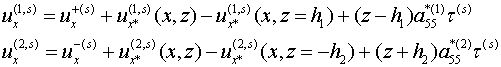           (1.11) 

  

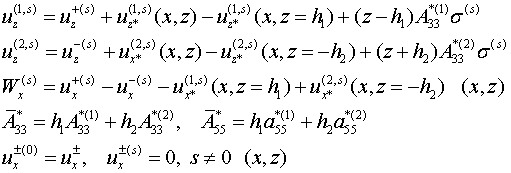
Все эти формулы сохраняют свой вид  и   при модели (1.2), и при модели (1.3), и вообще при любой модели неполного контакта. В зависимости от условий на линии (поверхности) контакта слоев меняются только касательное напряжение  и разность сдвиговых перемещений .  При модели (1.2) они имеют вид

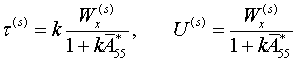                                       (1.12)

а при модели (1.3) они имеют вид

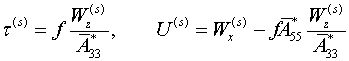                       (1.13)                                                    

И, поскольку расчетные рекуррентные формулы  (1.10),(1.11) после каждого шага итерации подразумевают одно дифференцирование по продольной координате и одно интегрирование по поперечной координате, они  приводят к замкнутому математическому решению краевой задачи для анизотропных полос и пластин бесконечных  продольных размеров после конечного числа шагов, когда заданные в уравнении и в граничных условиях функции являются полиномами продольных координат.

2.      Учитывая вышеизложенное рассмотрим  простейший случай, когда на продольных краях двухслойной полосы заданы постоянные перемещения                              (2.1)

и получено математически точное (замкнутое) решение.

а)  Из формул  (1.12) следует, согласно модели неполного контакта (1.2) отсутствие касательного перемещения приводит к отсутствию касательного напряжения

                                                      (2.2)

Это  вполне соответствует действительности, поскольку равномерно распределенные воздействия по направлению нормали продольного края полосы вызывают только сжатие или растяжение поперечных тканей материала полосы и не вызывают тангенциальных напряжений и перемещений  ее точек независимо от условий контакта слоев[1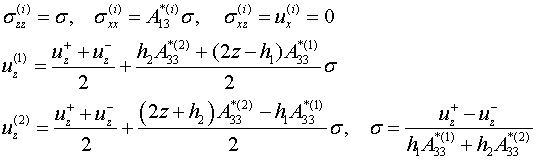-3]        (2.3)   

б) Согласно модели неполного контакта слоев (1.2)  касательное напряжение на линии контакта  определяется по формуле   

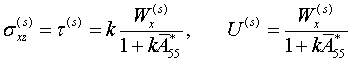                                   (2.4)

и непосредственно (при ) не связано с внешними воздействиями, направленными по нормалям продольных краев. Такая связь проявит себя начиная со второго шага итерации (), если эти внешние воздействия будут неравномерными.

в) Согласно модели неполного контакта (1.3) на линии контакта слоев касательное напряжение определяется формулой

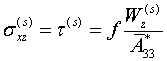                                                                               (2.5)

и в исходном шаге () итерации не зависит от параллельных продольным краям полосы внешних воздействий. Считаем, что такая модель уменьшает эффект шероховатости и не всегда соответствует реальной действительности.

Учитывая вышеизложенное, для неполного контакта ортотропных слоистых полос, пластин и оболочек предлагается линейный и нелинейные обобщенные модели, которые частично устраняют вышеуказанные недостатки.

3. Если предполагать, что на линии (поверхности) контакта слоев возникновению касательного напряжения способствуют и нормальное напряжение (закон сухого трения Кулона), и изменение касательных (сдвиговых) перемещений (аналогия гипотезы Винклера), то это может произайти по одной из следущих моделей:

а).                                                                             (3.1)

которое дает

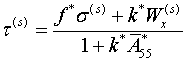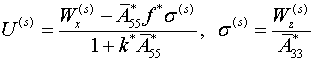,           (3.2)

б).   при                                                         (3.3)                                                        

при такой  нелинейной модели получаем

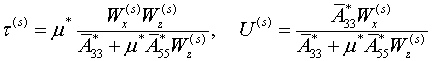                           (3.4)

в)     при                                  (3.5)                   

Такая нелинейная модель охватывает все предыдущие модели и дает ( )

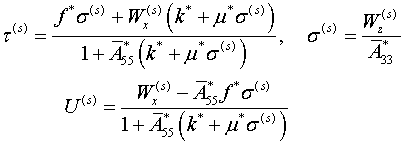                                   (3.6)

Преимущество предлагаемых обобщенных моделей очевидно, если для каждой пары контактирующих матералов слоев   коэффициенты  и   будут   определены экспериментально.

 

 

 

 

                                                    Литература

1. Агаловян Л. А.  О структуре решения одного класса плоских задач теории

    упругости анизотропного тела// Механика. Ереван: Изд-во ЕГУ, 1982.C.7–12.

2. Агаловян Л.А., Геворкян Р.С. Неклассические краевые задачи пластин с общей анизотропией //Сб. тр. 4-го Всес. Симп. по механике конструкций из композиционных материалов. Новосибирск: Наука, 1984. С.105–110.

3. Агаловян Л. А. Асимптотическая теория анизотропных пластин и оболочек. М: Наука.Физматлит, 1997.  414с.

4. Агаловян Л. А., Геворкян Р. С. Неклассические краевые задачи анизотропных слоистых балок, пластин и оболочек Ереван: Гитутюн, 2005. 468с.

5.Агаловян Л.А., Геворкян Р.С., Хачатрян Г.Г. Смешанные краевые задачи для анизотропных пластин переменной толщины // ПММ. 1996. Т.60. Вып.2. С. 290–298.

6. Агаловян Л.А., Халатян Л.М. Асимптотика вынужденных колебаний  ортотропной полосы при смешанных граничных условиях.// Докл. НАН РА 1999. Т.99, № 4.С.315–321.

7. Геворкян Р.С. Асимптотические решения установившичся динамических (связанных) задач термоупругости для изотропных пластин. // ПММ АН РФ.  2008.Вып.1. С.148-156.

8. Агаловян Л.А.,Геворкян Р.С. Асимптотические решения связанных динамических задач термоупругости для тонких тел из анизотропных, в плане анизотропных материалов//ПММ. 2011. Т.75. Вып. 5. С. 858-871.

9. Агаловян Л.А.,  Азатян Г.Л., Геворкян Р.С., Погосян А.М.  Об асимптотическом решении пространственной динамической задачи для прямоугольной пьезокерамической пластины// Доклады НАН РА  2011. Т.111,  № 2. С.129-137.

10 Гольденвейзер А.Л. Теория упругих тонких оболочек. М.: Наука, 1976. 512 с.

11. Зино И.Е., Тропп Э.А. Асимптотические методы в задачах теории

теплопроводности и термоупругости. Л.: Изд-во ЛГУ, 1978. 224 с.

12. Хачатрян А.М.  Об уравнениях  двухслойной анизотропной пластинки при нежестком контакте слоев.//Доклады НАН РА.1999. Т.99. №2. С.159-164.

13. Агаловян Л.А., Хачатрян А.М.  О двумерных уравнениях двухслойной анизотропной пластинки при неполном контакте между слоями// В сб.н.т. Контактные и смешанные граничные задачи механики деформируемого твердого тела. Ереван-1999. С.23-29.

14. Агаловян Л.А. Упругий пограничный слой для одного класса плоских задач// Меж. Вуз. Сборник н.трудов. Механика. Ереван: Изд-во ЕГУ, 1984. С.51-58.

15.  Геворкян Р.С. Асимптотика пограничного слоя для одного класса краевых задач анизотропных пластин //Изв.АН АрмССР.Механика.1984.Т.37.№6.С.3-15.