Технические науки/3. Отраслевое машиностроение

К.т.н. Гольдштейн Ю.М.

Институт технической механики НАНУ и ГКАУ, Украина

К вопросу о непараметрических моделях роста
надёжности для отработки эргатических систем

Непараметрические модели основываются на последовательности статистических оценок показателей надёжности, полученных после каждой серии проведённых доработок эргатической системы.

В биномиальной модели период испытаний разбивают на два этапа отработки, для которых характерны разные условия испытаний, так как отрабатываемое изделие изменяется в результате проведённой доработки. Предполагается, что испытания проводят по биномиальной схеме, причём на первом этапе в объёме испытаний зафиксировано отказ, а после проведения доработки на втором этапе в испытаниях зафиксировано отказа. Оценивается вероятность безотказной работы эргатической системы по результатам двух этапов испытаний с учётом различий условий их проведения. Для оценки этой вероятности рассматриваются четыре гипотезы.

Гипотеза . Для этой гипотезы условия испытаний остаются неизменными при переходе от одного этапа к другому, т.е. проведённые доработки не изменяют надежности эргатической системы. Эту гипотезу представим в виде .

Оценку вероятности безотказной работы в случае справедливости этой гипотезы, находят по формуле

. (1)

Гипотеза состоит в том, что после доработки надёжность эргатической системы может только увеличиваться, т.е. эту гипотезу можно записать в

следующем виде

Гипотеза . На втором этапе, т.е. после доработки, надёжность эргатической системы снижается. Гипотеза запишется так

Гипотеза . Отсутствует определённость в изменении условий испытаний после проведённой доработки, т.е.

Если условиям эксплуатации эргатической системы будет соответствовать второй этап испытаний, т.е. гипотезу отклоняют, то оценку вероятности безотказной работы находят из выражения

. (2)

Оценку вероятности безотказной работы эргатической системы по информации о двух проведённых этапах отработки находят по формуле

, (3)

где h - весовой коэффициент, равный вероятности выбора гипотезы ;

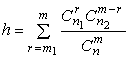, (4)

где , ,

При справедливости гипотезы значение вероятности расхождения двух групп данных определяют по формуле (4).

В случае справедливости гипотезы значение весового коэффициента . Наконец, для гипотезы значение весового коэффициента равно

. (5)

В триномиальной модели для оценивания уровня отработанности эргатической системы весь период испытаний делят на шагов, каждый из которых содержит определённый объем испытаний и заканчивается проведением доработки. Эта статистическая модель основана на том, что каждое испытание может иметь успех, случайный отказ, причина которого не установлена, и отказ, причина которого известна и устранима. В каждой серии испытаний фиксируют число случайных отказов, вероятность появления которых в течение всей отработки остаётся неизменной и равной . Вероятность устранимого отказа в процессе отработки имеет тенденцию к снижению, т.е. соответствующие вероятности образуют невозрастающую последовательность . Тогда оценку максимального правдоподобия для и определяют по формулам:

, (6)

где - оценка вероятности появления случайного отказа; - число случайных отказов, зафиксированных на -м этапе отработки; - объем испытаний за весь период отработки; - число этапов отработки;

, (7)

где , - оценка вероятности устранимого отказа на - м этапе отработки; - число устранимых отказов на - м этапе отработки; - объем испытаний на -м тапе отработки.

Если все оценки не возрастают, то их принимают в качестве окончательных; если же для некоторого - го этапа выполняется неравенство то наблюдения на этапах объединяют и вычисляют соответствующую оценку. Эту процедуру продолжают до тех пор, пока оценки не образуют невозрастающую последовательность. На основе полученных оценок определяют оценку вероятности успешной работы отрабатывемой эргатической системы на -м этапе по формуле

. (8)

Выражение (8) представляет собой триномиальную статистическую модель изменения надежности отрабатывемой эргатической системы.