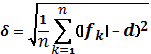Abstract:

Anomaly detection is a problem of finding unexpected readings in the measured data set. Whatever the cause of it, which is numerous, it must be detected and analyzed for accurate assessment of the expected behavior.

The current work developed novel methods to detect Anomalous patterns in temperature measurements or any similar time series. The proposed method is based on the analysis of the time series trend over time period. The proposed method has been compared to other famous detection methods and the result indicated that the trend analysis based detected the anomalous patterns more accurately; furthermore, the proposed method doesn’t need any additional parameters settings.

KEY WORDS: Anomalous; Outliers; modified Z-score; modified Thompson tau; modified boxplot, DBSCAN .

1. Introduction

Anomalous detection aims to find patterns in the measured data that do not conform to expected behavior. It has extensive use in many applications. But are not rigid mathematical definitions for constituting it; determining whether or not an observation is an anomalous is ultimately a subjective exercise. Many researches propose different techniques for anomalous detection [1]–[7]

These techniques include Parametric Statistical Modeling [8]–[11], Neural Networks [12]–[14], Spectral Techniques [15], Nearest Neighbor Based Techniques [16], Bayesian Networks [17], [18]and more.

Most of well-known anomalous detection techniques concerned in detecting the extremes values. But, they did not aware by the changing in series trend and direction.

This paper presents new methods for detecting anomalies in weather monitoring, specifically in air temperature measurements.

The series trend analysis is proposed to improve the accuracy of anomalous detection in air temperature measurements. However, they may be generalized to cover similar observations.

The following sections will describe in detail the proposed methods algorithm and methodology.

2. Time series trend analysis method

The proposed method depends on the analysis of the clustered time series trends. The main object of the proposed method is detecting two types of anomalous patterns:

- The extreme pattern (Type A): This refers to the data set that lay outside the expected boundaries of the measured data. These types of anomalies maybe considered as outliers.

- Trend anomalies (Type B): this refers to the deviation of the data pattern direction or shape. They may be considered as outliers or novelties.

3. The proposed method methodology

For simplicity the proposed method will be summarized in the following steps:

- Step 1: preparing the input data, which includes smoothing and clustering the input data using moving average method [19].

- Step 2: calculating the distance between each point and the nearest neighborhoods using the following equation:

f_k =2* y_k - (y_k+1 + y_k-1 )

(1)

Where: y(t): the smoothed input data, k=1:n and “n” is the measured data samples.

The average d of the distance function f will be calculated using the following equation:

d =

(2)

Then the residual E(t) will be calculated as follows:

E(t)= f(t) -sign( f(t) ).d

(3)

For ideal case, all residuals should be zero, if the measured data has not any anomalous or outliers. But that doesn’t happen in reality. The actual residuals may deviate within certain displacement threshold.

- Step 3: Threshold δ

In case of air temperature, δ will be equal the modified standard deviation of f(t):

(4)

The values of E will be categorized to three zones depending on δ according to the following classification :

When

(5)

The following section will summarize the experimental result for proposed algorithm.

4. Experimental results

The proposed method has been applied to a randomly selected sample of temperature measured data in a day (20 June 2014) and a week using DS18S20 sensors, which is a part of a full academic weather monitoring project. More details about the project can be found on the website “abc.altstu.ru”.

This sample has been divided into one hour time slots. Then the average for each slot has been calculated as well as f(t), d, E(t) and δ.

In figure 1, measured temperature y(t) and E(t) have been plotted using Matlab.

Type B

Type A

As shown in the figure, the measured data has the two types of anomalous data
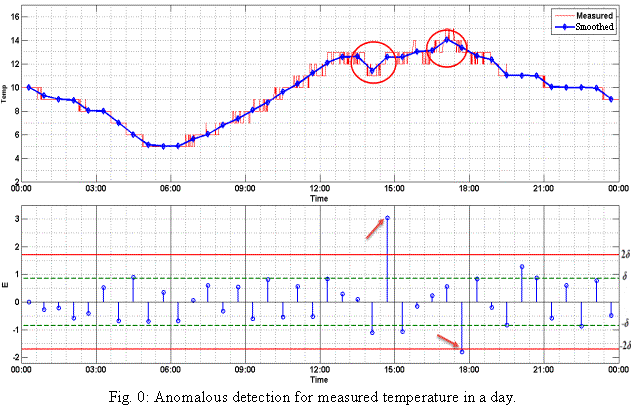
251669504“the highlighted area”; those are outside the boundary 2 δ.

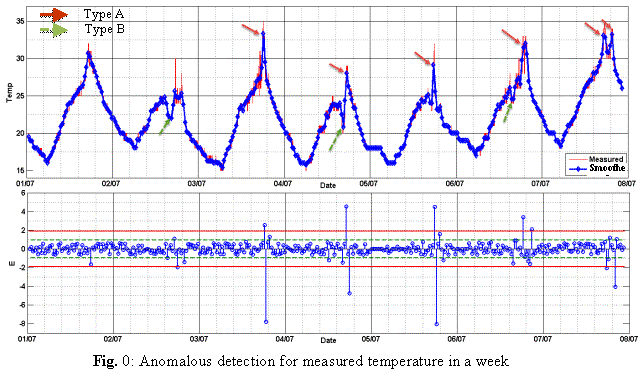
Also, the algorithm has been applied for one week sample measurement, the result showed that, the sample has many anomalies from both type A and B, as shown in figure 2.

5. Comparison with other detection techniques

The measured sampled have been tested with other techniques. Some of them (The adjusted boxplot [20] and the modified Thompson tau technique [21],) failed to detect these types anomalies, and the other (Z-scores [22] and DBSCAN [23]) detected only the type A anomalies with casting parameters .

6.
251670528251669504251671552Conclusion

The current work concluded that the trend analysis method was found to be quick and accurate method to detect outliers in air measurement data sets compared with the currently used methods. For future work, some techniques maybe developed, based on the proposed method, to determine whether the anomalies are outliers or novelties.

References:

[1] M. Sreedevi and D. S. Kumar, “Discovering Behavioral Characteristics of Anomalous Subpopulations,” vol. 1, no. 4, 2014.

[2] X. Song, M. Wu, C. Jermaine, and S. Ranka, “Conditional Anomaly Detection,” no. 0325459, pp. 1–14.

[3] P. Gogoi, D. K. Bhattacharyya, B. Borah, and J. K. Kalita, “A survey of outlier detection methods in network anomaly identification,” Comput. J., vol. 54, pp. 570–588, 2011.

[4] T. Idé, S. Papadimitriou, and M. Vlachos, “Computing correlation anomaly scores using stochastic nearest neighbors,” in Proceedings - IEEE International Conference on Data Mining, ICDM, 2007, pp. 523–528.

[5] J. M. Estevez-Tapiador, P. Garcia-Teodoro, and J. E. Diaz-Verdejo, “Anomaly detection methods in wired networks: A survey and taxonomy,” Comput. Commun., vol. 27, pp. 1569–1584, 2004.

[6] B. Hunt, “Climatic outliers,” Int. J. Climatol., vol. 27, pp. 139–156, 2007.

[7] V. Barnett, “The Study of Outliers: Purpose and Model,” J. R. Stat. Soc. Ser. C (Applied Stat., vol. 27, pp. 242–250, 1978.

[8] P. S. Horn, L. Feng, Y. Li, and A. J. Pesce, “Effect of outliers and nonhealthy individuals on reference interval estimation.,” Clin. Chem., vol. 47, pp. 2137–2145, 2001.

[9] H. E. Solberg and A. Lahti, “Detection of outliers in reference distributions: performance of Horn’s algorithm.,” Clin. Chem., vol. 51, pp. 2326–2332, 2005.

[10] D. A. Clifton, S. Hugueny, and L. Tarassenko, “Novelty detection with multivariate extreme value statistics,” J. Signal Process. Syst., vol. 65, pp. 371–389, 2011.

[11] E. Keogh, S. Lonardi, and B. “Yuan-chi” Chiu, “Finding surprising patterns in a time series database in linear time and space,” in Proceedings of the eighth ACM SIGKDD international conference on Knowledge discovery and data mining - KDD ’02, 2002, p. 550.

[12] T. C. Lu, J. C. Juang, and G. R. Yu, “On-line outliers detection by neural network with quantum evolutionary algorithm,” in Second International Conference on Innovative Computing, Information and Control, ICICIC 2007, 2008.

[13] Z. Bakar, R. Mohemad, A. Ahmad, and M. Deris, “A Comparative Study for Outlier Detection Techniques in Data Mining,” 2006 IEEE Conf. Cybern. Intell. Syst., pp. 1–6, 2006.

[14] S. S. Sane and A. A. Ghatol, “Use of instance typicality for efficient detection of outliers with neural network classifiers,” in Proceedings - 9th International Conference on Information Technology, ICIT 2006, 2007, pp. 225–228.

[15] V. Chatzigiannakis, S. Papavassiliou, M. Grammatikou, and B. Maglaris, “Hierarchical anomaly detection in distributed large-scale sensor networks,” in Proceedings - International Symposium on Computers and Communications, 2006, pp. 761–766.

[16] S. Subramaniam, T. Palpanas, D. Papadopoulos, V. Kalogeraki, and D. Gunopulos, “Online outlier detection in sensor data using non-parametric models,” VLDB ’06 Proc. 32nd Int. Conf. Very large data bases, pp. 187–198, 2006.

[17] S. Albrecht, J. Busch, M. Kloppenburg, F. Metze, and P. Tavan, “Generalized radial basis function networks for classification and novelty detection: Self-organization of optimal Bayesian decision,” Neural Networks, vol. 13, pp. 1075–1093, 2000.

[18] D. Janakiram, V. A. Reddy, A. V. U. P. V. U. P. Kumar, and A. M. R. V, “Outlier Detection in Wireless Sensor Networks using Bayesian Belief Networks,” in 2006 1st International Conference on Communication Systems Software & Middleware, 2006, pp. 1–6.

[19] C. Ya-Lun, Statistical Analysis, 2nd ed. Holt,Rinehart & Winston of Canada Ltd, 1975, p. 894.

[20] M. Hubert and E. Vandervieren, “An adjusted boxplot for skewed distributions,” Comput. Stat. Data Anal., vol. 52, pp. 5186–5201, 2008.

[21] W. R. Thompson, “On a Criterion for the Rejection of Observations and the Distribution of the Ratio of Deviation to Sample Standard Deviation,” Ann. Math. Stat., vol. 6, no. 4, pp. 214–219, Dec. 1935.

[22] R. E. Shiffler, “Maximum Z Scores and Outliers,” Am. Stat., vol. 42, pp. 79–80, 1988.