Кадыров А.С., Ганюков А.А., Нурмаганбетов А.C.

Карагандинский государственный технический университет, Казахстан

Нагружение гладкого цилиндра при движении

в глинистом тиксотропном растворе

Основной операцией при строительстве стен подземных сооружений, глубоких фундаментов или создание противофильтрационных завес является выкапывание узких глубоких траншей в грунте. Для устойчивости стенок траншеи во время отрывки грунта, траншею заполняют глинистым тиксотропным раствором, который, находясь в покое, образует студенистую массу – гель, а при механическом взаимодействии превращается в вязкую жидкость – золь. При этом рабочие органы траншейной машины работают в глинистом растворе и испытывают дополнительное давление со стороны раствора. Авторами проведены теоретические и экспериментальные исследования нагружения и напряженно-деформированного состояния рабочих органов бурильных и фрезерных машин при их движении в глинистом растворе[2]. Метод установления сил сопротивления, действующих на рабочий орган, а также напряженно-деформированного состояния рабочего органа, движущегося в глинистом растворе, заключается в его представлении совокупностью плоских тел и тел вращения.

В данном сообщении рассматривается модельная задача о движении гладкого цилиндра (вращательное и сложное) радиуса R и длиной L в глинистом тиксотропном растворе. Цилиндр приводится во вращение из состояния покоя с угловой скоростью . При движении цилиндра со скоростью, обуславливающей шведовский режим течения раствора [3], момент от силы сопротивления определяется следующим выражением:

(1)

где,

– площадь боковой поверхности цилиндра; – релаксационная вязкость; – относительная деформация; – начальный условно-мгновенный модуль сдвига; – модуль эластичности; – предел упругости, ниже которого остаточные деформации не развиваются; – время; – время релаксации.

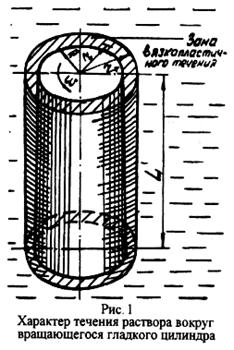Зона течения вязкопластичной жидкости распространяется лишь на конечное расстояние от вращающегося цилиндра (рис.1). Остальная часть раствора будет находиться в покое. Вокруг цилиндра образуется очень тонкий ламинарный слой, за которым находится зона вязкопластичного течения. Радиус зоны вязкопластичного течения и скорость движения жидкости связаны между собой зависимостями. При радиусе векторе , равном радиусу распространения зоны вязкопластичного течения , скорость движения раствора равна нулю, а при равенстве значений скорость движения раствора максимальна.

Градиент скорости сдвига по нормали:

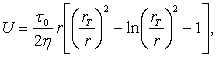
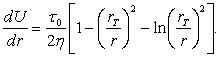(2)

где – скорость движения жидкости; – предельное напряжение сдвига; – структурная вязкость.

Момент сопротивления вращению цилиндра в глинистом тиксотропном растворе, при установившемся бингамовском режиме с учетом последеней зависимости в (2), выразится системой уравнений:

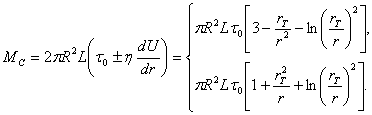(3)

Примем в дальнейшем максимальное значение момента, соответствующее сумме предельного касательного напряжения и произведения структурной вязкости на градиент скорости, с выполнением равенства , получим:

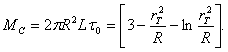(4)

В (4) момент сопротивления вращению цилиндра при бингамовском режиме течения раствора зависит от размеров цилиндра, предельного касательного напряжения сдвига и радиуса распространения зоны течения. Величина радиуса является функцией реологических характеристик раствора и угловой скорости движения цилиндра.

При псевдоламинарном режиме течения вязкопластичная жидкость по реологическим характеристикам адекватна вязкой жидкости с динамическим коэффициентом вязкости [3]. Вращение вязкой жидкости отличается от вращения твердого тела тем, что жидкость совершает динамическое вращение,
то есть частицы жидкости, удаленные на различное расстояние от оси
вращения, движутся с различными угловыми скоростями. При этом:

, (5)

где – окружная скорость жидкости; С – некоторая постоянная величина.

Следовательно, с удалением частиц раствора от оси вращения, их окружная скорость движения уменьшается за счет слоистого вращения и наличия трения между слоями. В пограничном слое и . Градиент скорости движения раствора: .

Сила трения по поверхности цилиндра с учетом равенства значений и определится выражением: , а момент от силы сопротивления: . При турбулентном режиме течения раствора момент сопротивления его вращению: , где – касательное напряжение сдвига определяется по зависимости:

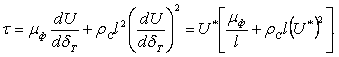(6)

Найдя градиент скорости движения раствора, получим:

. (7)

В случае сложного движения цилиндр вращается с постоянной угловой скоростью и движется со скоростью подачи . Для рабочих органов землеройных машин . В связи с этим силы сопротивления трению во вращательном движении значительно превышают силы сопротивления трению в поступательном движении. Поэтому с большой степенью точности для расчетов можно пользоваться зависимостями (3) и (5). В случае, если значения сравнимы со значениями скорости подачи, то необходимо учитывать угол между переносной и относительными скоростями.

Анализ полученных зависимостей позволяет сделать следующие выводы: при шведовском режиме течения глинистого раствора, сопротивление вращению цилиндра определяется упругими свойствами геля, при бингамовском – предельным сопротивлением сдвигу среды и размерами зоны вязкопластичного течения, при псевдоламинарном – динамической вязкостью раствора и скоростью его вращения.

Литература:

1. Смородинов М.И., Б.С. Федоров, Устройство сооружений и фундаментов способом «стена в грунте». – М.: Стройиздат, 1986. -216 с.

2. Кадыров А.С., Кабашев Р.А. Основы нагружения фрезерных и бурильных машин. – Караганда, КарГТУ, 1999. – 124с.

3. Огибалов П.М., Мирзаджанзаде А.Х. Нестационарное движение вязкопластичных сред. – М.: МГУ, 1970. – 415с.