Технические науки
Сурьянинов Н.Г.
Одесский национальный политехнический
университет, Украина
К расчету пластин,
подкрепленных ребрами жесткости,
методом граничных элементов
Дифференциальное уравнение изгиба ребристой пластинки
имеет вид
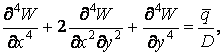 (1)
(1)
где ![]() — прогиб пластинки;
— прогиб пластинки; ![]() — свободный член
уравнения, учитывающий не только внешние нагрузки, но и наличие подкрепляющих
ребер в продольном направлении, под которым будем понимать направление,
параллельное оси y (рисунок 1).
— свободный член
уравнения, учитывающий не только внешние нагрузки, но и наличие подкрепляющих
ребер в продольном направлении, под которым будем понимать направление,
параллельное оси y (рисунок 1).

Рисунок 1 —
пластинка с ребром в продольном направлении
Наиболее общий вид ![]() имеет в том случае,
когда подкрепляющие ребра будут как сплошного сечения, так и тонкостенного:
имеет в том случае,
когда подкрепляющие ребра будут как сплошного сечения, так и тонкостенного:
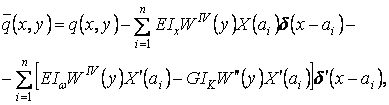 (2)
(2)
где ![]() — жесткости ребер при
изгибе и кручении;
— жесткости ребер при
изгибе и кручении;
![]() — координата расположения i-го ребра (рисунок 1).
— координата расположения i-го ребра (рисунок 1).
Применим для (1) метод Канторовича-Власова, т.е. прогиб срединной плоскости
пластинки будем искать в
виде
![]() (3)
(3)
Усечем ряд (3) до одного члена и возьмем вариацию прогиба только по
направлению y, что равносильно принятию расчетной
схемы пластины, имеющей бесконечное число степеней свободы в одном направлении
и одну степень свободы в другом направлении. Тогда прогиб точки срединной
плоскости пластины будет
![]() (4)
(4)
Функцию поперечного
распределения прогибов пластины ![]() нужно выбирать так,
чтобы она максимально точно описывала форму изогнутой поверхности пластины в
направлении оси х. Этому требованию в
полной мере удовлетворяют кривые прогиба балки, имеющей такие же условия
опирания, как и пластина, в направлении оси х.
нужно выбирать так,
чтобы она максимально точно описывала форму изогнутой поверхности пластины в
направлении оси х. Этому требованию в
полной мере удовлетворяют кривые прогиба балки, имеющей такие же условия
опирания, как и пластина, в направлении оси х.
В результате получим
задачу Коши одномерной модели изгиба прямоугольной пластины, подкрепленной
продольными ребрами:
![]() (5)
(5)
при
начальных условиях
![]()
![]()
![]()
![]() ; (6)
; (6)
где
![]()
![]()
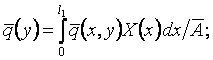 (7)
(7)
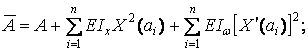 (8)
(8)
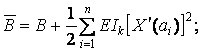 (9)
(9)
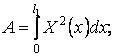
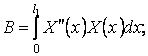
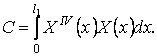 (10)
(10)
Дифференциальное
уравнение (5) по своей структуре аналогично уравнению, описывающему изгиб пластин без подкреплений, однако
вид (7)-(9) свидетельствует о том, что в (5) учтены параметры ребер. Применительно
к реализации алгоритма метода граничных элементов это означает, что параметры
ребер будут учтены и в выражениях фундаментальных функций.
Решение задачи Коши (5)-(6) можно представить в соответствии с
алгоритмом метода граничных элементов:
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
Таким
образом, при использовании метода Канторовича-Власова решение основного
дифференциального уравнения задачи сводится к определению прогиба (4), где
функция ![]() задана, а
задана, а ![]() определяется из (11) в
виде
определяется из (11) в
виде
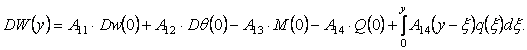 (12)
(12)
Решение уравнения (5)
зависит от корней соответствующего ему характеристического уравнения, которые
представляются выражением
![]() (13)
(13)
Вид
фундаментальных функций определяется соотношением между r и s,
которое зависит от граничных условий на продольных кромках пластины. При этом
здесь возможны шесть случаев.
Рассмотрим
вариант, когда ![]() , при этом
, при этом
![]()
где 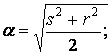
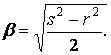
Прогиб ![]() запишется в виде
запишется в виде
![]() (14)
(14)
где ![]() —
гиперболо-тригонометрические функции:
—
гиперболо-тригонометрические функции:
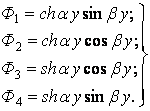 (15)
(15)
Фундаментальные функции задачи, получение которых
аналогично описанному в [1, 2], предстанут в форме:
 (16)
(16)
 (17)
(17)
Литература:
1.
В.А. Баженов, А.Ф. Дащенко, Л.В. Коломиец, В.Ф.
Оробей, Н.Г. Сурьянинов / Численные методы в
механике. — Одесса, «СТАНДАРТЪ», 2005. — 563 с.
2. Оробей В. Ф., Работягов Д. Д. Расчет пластин на изгиб одномерным
вариантом метода граничных интегральных уравнений // Изв. вузов. Строительство.
— 1993. — № 1. — С. 20-27.