Степанова Н.В., д.ф.-м.н. Терпугов А.Ф.
Алтайский
экономико-юридический институт, Россия
Управление ценой при продаже скоропортящейся
продукции
Оптимизация
продажи скоропортящейся продукции (молоко, творог и т.д.) представляет
определенный практически интерес, так как продукцию, не реализованную в течение
торговой сессии, в лучшем случае надо пускать в переработку, а в худшем случае
– просто выбрасывать. Поэтому при реализации такой продукции возникает ряд
вопросов, таких как
а) какой объем
продукции надо завозить на торговую точку;
б) по какой цене
ее продавать;
в) как управлять ценой продажи продукции, чтобы к концу торговой сессии
она была полностью реализована.
Все эти задачи
надо решать при вполне естественном критерии оптимальности – максимизации прибыли,
получаемой от реализации продукции.
Математическая модель
Пусть в торговую
точку завозится партия продукции объемом Q0, которая должна быть продана в течение торговой сессии
длительности Т. Пусть d – объем затрат на выпуск единицы
продукции, так что производителю эта партия стоила Q0 d рублей.
Пусть c(t) есть цена, по которой продукция продается в момент времени t. В данной работе
рассматривается вопрос управления ценой продажи c(t) в
зависимости от времени t и
объема Q(t) продукции, не реализованной к этому моменту времени. Цель
этого управления – добиться того, что продукция будет реализована к концу торговой
сессии и при этом будет получена максимальная прибыль.
Будем считать,
что поток покупателей является пуассоновским потоком интенсивности l(с), зависящей
от розничной цены с. Вид этой
зависимости будет уточнен ниже.
Будем считать,
что покупатели покупают товар независимо друг от друга, и объем покупки x есть случайная величина с ![]() и
и ![]() .
.
Пусть Q(t) есть количество продукции, которая осталась не
реализованной в момент времени t.
Рассмотрим решение задачи в так называемом диффузионном приближении, когда Q(t) аппроксимируется диффузионным случайным процессом. Как
показано Е.В. Новицкой, такую аппроксимацию следует брать в виде
![]() , (1)
, (1)
где ![]() – стандартный
винеровский процесс. Именно эту аппроксимацию мы и исследуем ниже.
– стандартный
винеровский процесс. Именно эту аппроксимацию мы и исследуем ниже.
В настоящей работе будет исследован случай, когда
управление розничной ценой определяется соотношением
![]() (2)
(2)
Объединяя (1) и (2) можно
сказать, что диффузионная аппроксимация процесса Q(t)
имеет вид
![]() . (3)
. (3)
Найдем сначала
некоторые характеристики процесса Q(t).
Математическое
ожидание процесса Q(t)
Обозначим ![]() . Для краткости записи, аргумент t у Q(t) и
. Для краткости записи, аргумент t у Q(t) и ![]() мы часто будем
опускать. Усредняя уравнение (3) с учетом того, что для винеровского случайного
процесса
мы часто будем
опускать. Усредняя уравнение (3) с учетом того, что для винеровского случайного
процесса ![]() , получим
, получим
![]() ,
(4)
,
(4)
Решение этого уравнения
имеет вид
![]() . (5)
. (5)
Дисперсия
процесса Q(t)
Обозначим ![]() . Можно показать, что эта величина удовлетворяет уравнению
. Можно показать, что эта величина удовлетворяет уравнению
![]() . (6)
. (6)
Нас будет интересовать
дисперсия процесса Q(t), то есть процесс ![]() . Решая уравнение (6) с начальным условием
. Решая уравнение (6) с начальным условием ![]() , можно получить
, можно получить
![]() . (7)
. (7)
Математическое
ожидание выручки и его оптимизация
Рассмотрим случай, когда зависимость l(с) может
быть аппроксимирована прямой линией
![]() .
(8)
.
(8)
Здесь с0
имеет смысл некоторой «стандартной» цены, так что ![]() . Такая аппроксимация возможна, если отклонения цены с от с0
незначительны.
. Такая аппроксимация возможна, если отклонения цены с от с0
незначительны.
В этом случае уравнение (2) приобретает вид
![]() ,
,
откуда
![]() . (9)
. (9)
Так как в единицу времени в
среднем совершается l(с) покупок, средний размер которых равен а1 по цене с,
то среднее значение выручки в единицу времени равно
![]() .
(10)
.
(10)
Усредняя по объему партии
товара Q(t), имеющегося в наличии в момент времени t, получим
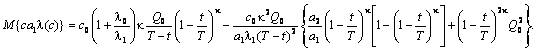 (11)
(11)
Отсюда средняя выручка за
весь период торговой сессии равна ![]() .
.
Вычисляя входящие сюда интегралы, получим
![]() . (12)
. (12)
Задача выбора оптимального
значения k пронимает вид
![]() ,
,
Приравнивая нулю производную
от этого выражения по k, получим
![]() , (13)
, (13)
которое надо решить в
области k > 1.
Можно показать, что это уравнение имеет единственное решение.
Определение
оптимального объема партии товара, выставляемой на продажу
Существует также
оптимальный объем партии товара Q0,
выставляемый на продажу. Так как себестоимость единицы продукции равна d, то прибыль, получаемая от
продажи партии товара объема Q0 равна
(с учетом (11))
![]()
![]() ,
,
и оптимальный объем партии Q0 определяется из условия ![]() :
:
![]() =
=![]() . (14)
. (14)
Можно решать и более глобальную оптимизационную задачу
– максимизацию прибыли по величинам Q0 и
k. Это означает, что мы должны решать совместно систему
(13) и (14).
 (15)
(15)
Эта система также имеет единственное решение.