Математика/Прикладная математика

Д.ф.-м.н. Емец О.А., Устьян Н.Ю.

Полтавский университет потребительской кооперации Украины

Метод нахождения оптимальной стратегии игрока

в игровых комбинаторных задачах на перестановках

В [1] была построена математическая модель игровой задачи с комбинаторными ограничениями на использования стратегий одним игроком. Для нахождения оптимальной стратегии игрока, на стратегии которого накладываются комбинаторные ограничения, нужно решить такую задачу комбинаторной оптимизации на перестановках (для модели, приведенной в [1], было учтено, что и обозначено ):

(1)

Алгоритм решения задачи

1. Упорядочим коэффициенты при фиксированных и элементы множества по возрастанию: полученные элементы обозначим и соответственно. Вычислим и

2. Сначала выбираем

3. Решаем такую задачу комбинаторной оптимизации на перестановках:

Пусть

4. Для точки находим значения и Присваиваем значение и рассматриваем

5. Пусть

6. Если условие выполняется, переходим на шаг 9, если нет – на шаг 7.

7. Решаем такую задачу комбинаторной оптимизации на перестановках:

(2)

Пусть – решение задачи (2).

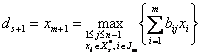8. Для точки находим значения и Присваиваем значение Увеличиваем на 1, переходим на шаг 6.

9. Выбираем – решение исходной задачи.

Для решения задачи комбинаторной оптимизации на перестановках (2) на етапе 7 можно использовать метод решения систем неравенств, описанный в [2, стр.255-260]. Рассмотрим перестановочный многогранник [см., напр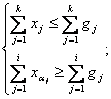. 3]:

(3)

и систему неравенств

(4)

Доказаны следующие теоремы:

Теорема 1: Вершины перестановочного многогранника (3) являются фундаментальными решениями системы неравенств (4).

Теорема 2: Фундаментальные решения системы (4) существенно различны.

Теорема 3: Кроме вершин перестановочного многогранника других фундаментальных решений система неравенств (4) не имеет.

Тогда, согласно определению фундаментальной системы решений системы неравенств [2, стр. 162], вершины перестановочного многогранника составляют фундаментальную систему решений системы неравенств (4) (доказано, что это утверждение справедливо и для системы неравенств (3)). Также доказано, что произвольное решение системы неравенств (3) выражается формулой , где – произвольные неотрицательные элементы поля , а – вершины перестановочного многогранника (3).

Согласно Теореме 3.2 [2, стр. 234] при добавлении к системе неравенств (4) нового неравенства в фундаментальную систему решений новой системы неравенств войдут все фундаментальные решения системы неравенств (4), для которых и те элементы с , для каждого из которых существуют линейно независимых неравенств обращающихся в равенства как для так и для Доказано, что 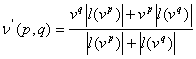тоже будут являтся фундаментальными решениями новой системы неравенств, не существенно различными для и можно заменить на Также доказано, что соседние вершины перестановочного многогранника обращают в равенства неравенства системы (4) с линейно независимыми левыми частями, и никакие другие фундаментальные решения этой системы не обращают в равенства эти неравенства, и является точкой пересечения двух соседних вершин перестановочного многогранника (3), из которых одна не удовлетворяет неравенство , а вторая удовлетворяет, и гиперплоскости . Из этого следует, что в фундаментальную систему решений новой системы неравенств при добавлении дополнительного неравенства войдут все фундаментальные решения (вершины перестановочного многогранника (3)), которые удовлетворяют этому неравенству, а также элементы которые не являются вершинами и их включать в новую фундаментальную систему не будем. Тогда в фундаментальную систему решений системы неравенств (4) (и (3)) с дополнительнимы неравенствами войдут лишь те вершины перестановочного многогранника (3), которые удовлетворяют всем неравенствам

Доказано, что для решения задачи комбинаторной оптимизации (2) можно использовать метод нахождения общей формулы решений системы линейных неравенств Черниковой Н.В. [2, стр. 255-260] со следующими изменениями:

1. Назовем строками, дающими перестановки, те строки таблицы , у которых в одном из столбцов таблицы , соответствующих дополнительных ограничениям, стоит 1, а во всех остальных столбцах – 0. В качестве основных столбцов в таблицах сначала нужно выбирать все столбцы, которые соответствуют неравенствам, определяющим перестановочный многогранник (3); при выборе основными столбцами столбцов, соответствующих дополнительным ограничениям, в следующую таблицу переносятся только те строки равновесия, у которых одной из уравновешенных допустимых строк является строка, дающая перестановки.

2. При переходе от таблицы к в таблице в строках равновесия в столбцах, соответствующих , элементы будут равны 0, если оба соответствующих элемента допустимых строк равны 0; и 1 – в противоположном случае (их реальные значения нам не нужны).

Литература:

1. Ємець О.О., Устьян Н.Ю. Ігрова комбінаторна модель однієї задачі сільськогосподарського виробництва //Матеріали VII Міжнародної науково-практичної конференції "Наука і освіта '2004" – Дніпропетровськ: Наука і освіта, 2004, том 70 – С.46-49

2. Черников С.Н. Линейные неравенства. – М.: Наука, 1968. – 488 с.

3. Стоян Ю.Г., Ємець О.О. Теорія і методи евклідової комбінаторної оптимізації. – К.: ІСДО, 1993. – 188 с.

Емец О.А. Устьян Н.Ю.