Математика / 1

Рашевський М.О.

Криворізький технічний університет

Асимптотичне інтегрування систем лінійних інтегро-диференціальних рівнянь із точками повороту

 

Асимптотику розв’язку задачі Коші 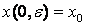 для системи вигляду

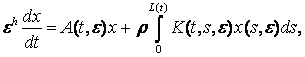                                      (1)

побудовано у ряді досліджень (див. напр., [1]). Тут x(t, e) – шуканий n – вимірний вектор, A(t, e) та K(t, s, e) – n ´ n – матриці, що зображуються збіжними рядами за степенями дійсного малого параметра e > 0: 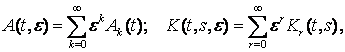 h > 0 – раціональне число. Розглянуто випадки L(t) º t та L(t) º L. При цьому вимагалося, щоб корені характеристичного рівняння  зберігали постійну кратність на проміжку t Î [0, L], L < ¥; , E – одинична матриця.

У ряді практичних застосувань систему (1) необхідно досліджувати при наявності нестабільностей у спектрі матриці A(t, 0) [3]- [5], і, зокрема, точок повороту (ТП). У цьому дослідженні методи [4, 5], розроблені для систем звичайних диференціальних рівнянь, застосовуються для інтегрування системи (1) із ТП. Вимагатимемо виконання таких умов.

          10. Матриці Ap(t) та Kp(t, s) є нескінченно диференційовними відповідно на проміжку [0, L] та в квадраті R = {0 £ t, s £ L}; p ³ 0.

20. Корені характеристичного рівняння R(l, t, 0) є різними при t Î [0, L] / {t = t0} і збігаються при t = t0, t0 Î [0, L].

Нехай L(t) º L. Формальний розв’язок системи (1) шукатимемо у вигляді

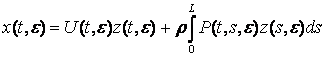,                               (2)

де z(t, e) – n – вимірний вектор, U(t, e) та P(t, s, e) – невідомі n ´ n –матриці. Підставляючи (2) у рівняння (1), після зміни порядку інтегрування в повторному інтегралі, дістанемо:

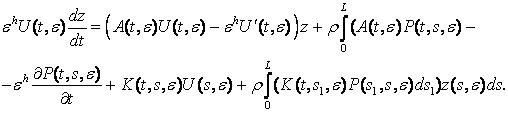
          Матриці U(t, e) та P(t, s, e)  будуватимемо так, щоб мали місце тотожності

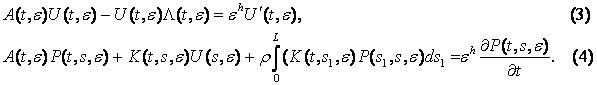
Побудова матриць U(t, e) та P(t, s, e) істотно залежить від характеру нестабільності спектра матриці A0(t), а також рангу h системи. У цій роботі розглянемо випадок майже діагональної [5] матриці A(t, e). Нехай h = 1, і виконується умова

30. A0(t0) подібна діагональній матриці p0E, p0 ¹ 0 – комплексне число.

З останньої умови випливає існування неособливої матриці T(t) такої, що

T -1A0(t)T = diag {l1(t), l2(t), …, ln(t)} = L(t); L(t0) = p0E.

Будуватимемо невідомі матриці у вигляді 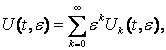 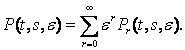 Щоб задовольнити тотожність (3), розв’яжемо систему матричних рівнянь, яку отримаємо після підстановки U =TQ, прирівнюючи коефіцієнти при степенях e:

A0(t)Q0 – Q0L0(t) = e Q0¢

(5)

A0(t)Qs – QsL0(t) = e Qs¢ + Fs(t) – U0Ls(t),  s = 1, 2, …

З першого рівняння системи (5) знайдемо Q0(t)=E. Для визначення кожної з матриць Qs(t) маємо n2 скалярних диференціальних  рівнянь першого порядку:

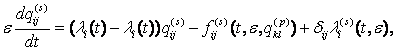                      (6)

де - (i, j)- елементи матриць Fs, Qs, Ls; i, j, k, l = , s ³ 1, 0 £ p < s.

Нехай . Тоді . Знайдемо

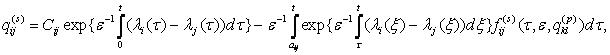
де aij, Сij - константи, які вибиратимемо так: aij = 0, Сij  = 0, якщо

Re(li(t) - lj(t)) £ 0, a = L, Сij = Сij(e), якщо Re(li(t) - lj(t)) > 0; Сij(e) знайдемо з умови . Випадок зміни знаку функціями Re(li(t) - lj(t)) на проміжку побудови асимптотики вимагає залучення багатомасштабного методу.

Прирівнюючи коефіцієнти при однакових степенях e у тотожності (4), дістанемо нескінченну систему матричних інтегральних рівнянь

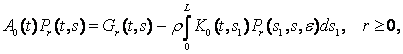 де

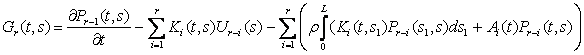
Позначивши через G(t, s, r) резольвенту ядра  із згаданих рівнянь отримаємо матриці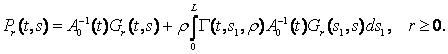

Після такого визначення коефіцієнтів системи (2), остання з точністю до 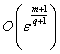 інтегрується  в квадратурах. Початкові умови визначаться із рівності .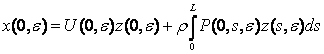

Описані побудови формальних розв’язків системи (1) сформулюємо у вигляді теорем.

Теорема 1. Якщо виконуються умови 10-30 і r - регулярне значення ядра A0-1(t)K0(t, s), то система (1) при L(t) º L і h = 1 має формальний розв’язок вигляду (2).

Теорема 2. Якщо виконуються умови теореми 1, і Re l k(t) £ 0, то для m – наближення xm(t, e), (xm(0, e) = x0) отриманого із (2), існує деякий точний розв’язок x(t, e) такий, що

де C – стала, що не залежить від e.

Виродження матриці A0(t) в окремих точках призводить до того, що система інтегральних рівнянь для визначення Pr (t, s, e), яка є системою третього роду, має розв’язки у класі узагальнених функцій [2, 3].

Розглянемо систему інтегральних рівнянь Фредгольма третього роду:

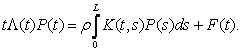                                  (7)

Будуватимемо розв’язок останньої у вигляді, де C – стала матриця, d p(t) – «права дельта – функція» [2], Y(t) – матриця із неперервними елементами. Підставляючи матрицю P(t) в систему (7), дістанемо рівність

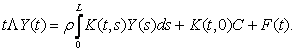
Поклавши в останній рівності t = 0, матимемо: 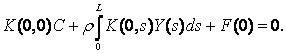 З останньої рівності дістанемо:  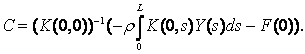Отримана система інтегральних рівнянь

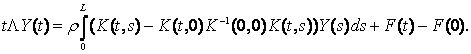
є системою Фредгольма другого роду із неперервними коефіцієнтами (t = 0 є точкою усувного розриву). Нехай Y(t) – неперервний розв’язок останнього рівняння. Тоді матриця C визначиться нульовою, якщо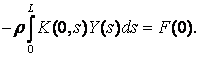

Виходячи з цих міркувань, необхідно тотожність (5) замінити наступною

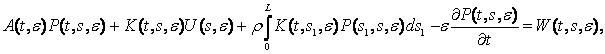і будувати Wk(t, s, e) так, щоб забезпечити неперервність Pk(t, s, e), які визначаться із системи рівнянь

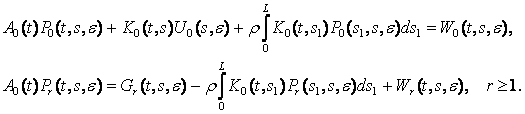
Принципова можливість такої побудови матриці W(t, s, e) випливає із наведених вище міркувань, але алгоритм побудови не розроблено. Якщо иатрицю W(t, s, e) визначено, то невідомий для вектора z(t,e) дістанемо систему інтегро – диференціальних рівнянь

 

 

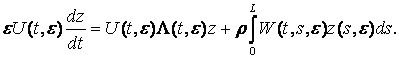
Література

1.     Завізіон Г.В. Асимптотичне інтегрування систем інтегро-диференціальних рівнянь з виродженнями // УМЖ.- 1999.- № 2.- С. 170 - 180.

2.     Иманалиев М.И. Обобщенные решения интегральных уравнений первого рода. - Фрунзе: «Илим», 1981. – 144 с.

3.     Новаковская Л.И. Задача Коши для сингулярно возмущенного интегро-дифференциального уравнения с нестабильным спектром // ДУ.- 1989.- 25, № 9.- С. 1606 - 1611.

4.     Шкиль Н.И. О периодических решениях систем дифференциальных уравнений второго порядка // Arch. Math. (Brno). - 1987. - 23, № 1. - P. 53-62.

5.     Wasow W. Linear Turning Point Theory. – N.Y.: Acad. Press, 1985. – 246 p.