Математика
/ 1. Дифференциальные и интегральные уравнения
Кульжумиева А.А., Сартабанов Ж.А.
Актюбинский государственный
университет им. К. Жубанова, Казахстан
Периодические по многомерному
времени решения линейных систем ![]() -уравнений
-уравнений
1. Постановка задачи. Рассмотрим оператор дифференцирования ![]() по многомерному времени
по многомерному времени ![]() в направлении
постоянного вектора
в направлении
постоянного вектора ![]() . Следовательно, имеем
. Следовательно, имеем ![]() ,
где
,
где ![]() ,
, ![]() . В дальнейшем положим
. В дальнейшем положим ![]() ,
, ![]() ,
, ![]() . Вектор-функцию
. Вектор-функцию ![]() назовем
характеристикой оператора
назовем
характеристикой оператора ![]() .
.
Теперь введем в
рассмотрение систему квазилинейных дифференциальных уравнений вида
![]() , (1)
, (1)
где ![]() .
.
Вектор-функция ![]() задана для
задана для ![]() и обладает свойством
периодичности по
и обладает свойством
периодичности по ![]() с периодом
с периодом ![]() , по
, по ![]() , следовательно и по
, следовательно и по ![]() с вектор-периодом
с вектор-периодом
![]() , непрерывности по всем аргументам и непрерывной
дифференцируемости по
, непрерывности по всем аргументам и непрерывной
дифференцируемости по ![]() ,
, ![]() ,
, ![]() . Следовательно, имеем
. Следовательно, имеем
![]() , (2)
, (2)
где ![]() – множество
целочисленных векторов
– множество
целочисленных векторов ![]() ,
, ![]() – кратный вектор-период,
а
– кратный вектор-период,
а ![]() – положительно
определенная
– положительно
определенная ![]() -периодическая и непрерывно дифференцируемая функция
-периодическая и непрерывно дифференцируемая функция
![]() ,
,
причем ![]() ,
, ![]() – положительные
рационально несоизмеримые постоянные.
– положительные
рационально несоизмеримые постоянные.
При
этих условиях ставится задача о существовании ![]() -периодических
по
-периодических
по ![]() решений системы (1).
решений системы (1).
Заметим [1], что для
достижения этой цели нам достаточно ограничиться решениями системы (1),
удовлетворяющими начальным условиям вида
![]() ,
(10)
,
(10)
где ![]() – пространство
непрерывно дифференцируемых
– пространство
непрерывно дифференцируемых ![]() -периодических
-периодических ![]() -вектор-функций
с нормой
-вектор-функций
с нормой ![]() при
при ![]() :
:
![]() .
.
Здесь ![]() – знак евклидовой
метрики.
– знак евклидовой
метрики.
Под интегралом функции ![]() вдоль характеристики
вдоль характеристики ![]() ,
, ![]() оператора
оператора ![]() от точки
от точки ![]() до точки
до точки ![]() пространства
многомерного времени
пространства
многомерного времени ![]() понимаем соотношение
понимаем соотношение 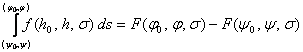 , где
, где ![]() – интеграл функции
– интеграл функции ![]() по параметру
по параметру ![]() [2]. В частности,
решение
[2]. В частности,
решение ![]() задачи (1)-(10) определяется
интегральным уравнением
задачи (1)-(10) определяется
интегральным уравнением
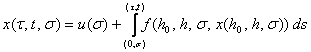 ,
(3)
,
(3)
где ![]() .
.
Теперь основную задачу
исследуем для линейного случая.
2. Периодические по многомерному времени решения линейных
систем. Рассмотрим
линейную систему
![]() (4)
(4)
с ![]() -матрицей
-матрицей ![]() непрерывно
дифференцируемой и
непрерывно
дифференцируемой и ![]() -периодично определенной на характеристике
-периодично определенной на характеристике ![]() . Следовательно,
. Следовательно,
![]() , (5)
, (5)
причем
собственные значения ![]() матрицы
матрицы ![]() при любых значениях
при любых значениях ![]() не принимают значения
равные
не принимают значения
равные ![]() :
:
![]() . (6)
. (6)
При
предположениях (5) и (6) матрицант ![]() однородной системы
однородной системы
![]() (7)
(7)
обладает
свойствами
![]() ,
,
причем
матрица монодромии ![]() не имеет единичного
мультипликатора
не имеет единичного
мультипликатора ![]() при любых
при любых ![]() . Следовательно, в силу обратимости матрицы
. Следовательно, в силу обратимости матрицы ![]() и представления
решения
и представления
решения ![]() системы (7) с
начальным условием (10) в виде
системы (7) с
начальным условием (10) в виде
![]() , (8)
, (8)
она не имеет ![]() -периодического
по
-периодического
по ![]() решения, кроме
тривиального.
решения, кроме
тривиального.
Тогда легко показать, что
линейная система (4) с вектор-функцией
![]() , (9)
, (9)
имеет
единственное ![]() -периодическое
по
-периодическое
по ![]() решение
решение ![]() , представимое в виде
, представимое в виде
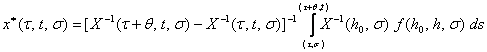 . (10)
. (10)
Полученный результат
сформулируем в виде следующего утверждения.
Теорема. Пусть выполнены условия (5), (6) и
(9). Тогда неоднородная система дифференциальных уравнений (4) с многомерным
временем ![]() имеет единственное
имеет единственное ![]() -периодическое решение
-периодическое решение ![]() , представимое в виде (10).
, представимое в виде (10).
Единственность
периодического решения системы (4) доказывается отсутствием ненулевого
периодического решения однородной системы (7).
Данное исследование
является продолжением исследований, предложенных в [3-5].
Литература:
1.
Сартабанов Ж.А. Условия периодичности решений
дифференциальных систем с многомерным временем // Известия НАН РК Сер.
физ.–мат., 2004, №3. С. 44-48.
2.
Сартабанов Ж.А., Кульжумиева А.А., Калыбаева
Д.Т. Об интеграле функции многомерного времени // Вестник АГУ, 2004, №4. С.
3-7.
3. Кульжумиева
А.А., Сартабанов Ж.А. Многопериодические
решения систем дифференциальных уравнений с многомерным временем и переменным
периодом // Тез. докл. Междунар. матем. конф. «Еругинские чтения – Х».
24-26 мая 2005. – Могилев. С. 71-72.
4.
Kulzhumiyeva
A., Sartabanov Zh. On
periodic solutions of the nonlinear system of the differential equations with
multivariate time and variable period // International Scientific Conf.
«Mathematical analysis, differential equations and their applications».
5. Кульжумиева
А.А., Сартабанов Ж.А. Голоморфность
периодических колебаний в нелинейной системе многомерного времени с переменным
периодом относительно малого параметра // Матерiали III Мiжнародної науково-практичної
конф. «Науковий потенцiал
свiту
– 2006». 18-29 вересня 2006 року. Т.1. – Днiпропетровск.
С. 5-8