Ващенко Г.В., Молодцов И.А.

Сибирский государственный технологический университет, Россия

Численные исследования одного класса матриц для больших разреженных систем

Необходимость решения больших разреженных систем линейных алгебраических уравнений связана с тем, что математические модели многих практических задач, в конечном счете, сводятся к моделям на основе систем с большими и разреженными матрицами коэффициентов.

В работе рассматривается набор тестовых матриц M(n,k1,k2) и результаты численных экспериментов с помощью программного обеспечения разработанного специально для целей численного исследования.

Как правило, утверждения или предположения о численных методах для разреженных матриц, не удается доказать математически. Для того чтобы выяснить при каких обстоятельствах они лучше работают основываются на результатах численных экспериментов. С этой целью строятся тестовые матрицы. В настоящей работе рассматриваются тестовые матрицы класса M(n,k1,k2). Это квадратные матрицы с тремя главными диагоналями и набором элементов, количество которых зависит от параметров k1,k2. Портрет матрицы М(8, 2, 3) показан на рисунке 1. Меняя k₁ k₂ n, можно получить матрицы разных размеров и различной структурой разреженности.

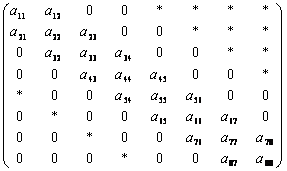
Рисунок 1- Портрет матрицы М(8, 2, 3)

На рисунке 1 звездочкой обозначены элементы отличные от 0.

Для решения систем уравнений использовался классический метод итераций Гаусса-Зейделя, схема которого имеет вид [4]:

x^(k+1) = (E – (G + L)^-1·A)·x^(k) + (G + L)^-1·b , k = 0,1,…,

где E – единичная матрица, G – диагональная матрица и L – нижнетреуголь-ная части матрицы А.

Укрупненная схема программного обеспечения состоит из блоков формирования исходной матрицы А по параметрам n,k1,k2, вычислений по схеме метода Гаусса-Зейделя и вывода результатов вычислений.

Критерием окончания итераций в реализации служило условие , где - евклидова норма.

При анализе вычислений главное внимание было уделено количеству итераций, необходимых для достижения заданной точности, поведению погрешности и дополнительно число арифметических операции..

Все вычисления проводились с точностью 0,001, все числа в программе типа Double. Элементы формировались по правилу:

a_ii = 100·i+i·10, a_ij = (i·2+j) mod 10 + 1, для i ¹ j. Вычисления проводились на машине с процессором AthlonXP 1533 MHz. Программный комплекс реализован в системе Delphi 5. На рисунках 1, 2 приведены графики иллюстрирующие поведение погрешности при заданных параметрах n,k1,k2.

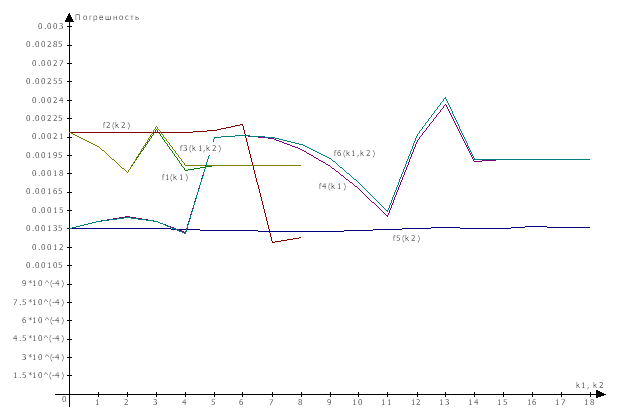
Рисунок 2 – График поведения погрешности решения при малых изменениях n ,k1, k2

На рисунке f_i обозначает результат i-го эксперимента, а элементы исходной матрицы принимались большими 1.

f1(n,k1,k2): n = 10, k2 = 0, k1 = 0, 1,…, 8; f2(n,k1,k2): n = 10, k1 = 0, k2 = 0, 1,…, 8;

f3(n,k1,k2): n = 10, k2 = k1 = 0, 1, …, 8; f4(n,k1,k2): n = 20, k2 = 0, k1 = 0, 1, …, 18,

f5(n,k1,k2): n = 20, k1 = 0, k2 = 0, 1, …, 18; f6(n,k1,k2): n = 20, k2 = k1 = 0, 1, …, 18.

На рисунке 3 график поведения погрешности при следующих исходных данных: с элементами больше 1 и следующими параметрами для формирования матрицы A:

f7(n,k1,k2): n = 100, k2 = 0, k1 = 0, 1,…, 98; f8(n,k1,k2): n = 100, k1 = 0, k2 = 0,1,…, 98

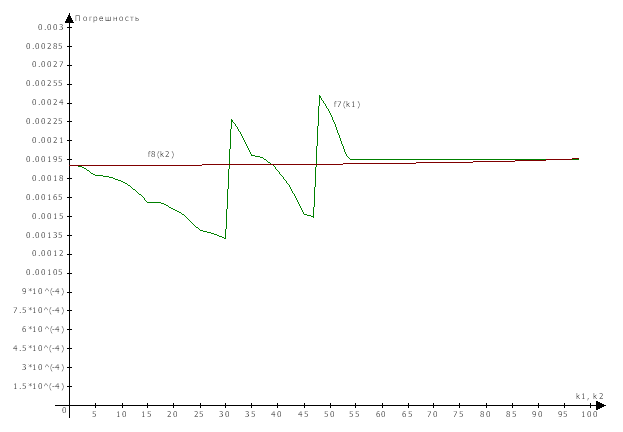
Рисунок 3 – График поведения погрешности решения при больших изменениях n,k₁,k₂.

Литература:

1. Ортега Дж. Введение в параллельные и векторные методы решения линейных систем. - М.: Мир, 1991.- 365 с.

2. Джордж А., Лю Дж. Численное решение больших разреженных систем уравнений. - М.: Мир, 1984. - 428 с.

3. Писсанецки С. Технология разреженных матриц. - М.: Мир, 1988.

4. Безруких Н.С., Ващенко Г.В. Вычислительная математика. Итерационные методы решения систем линейных алгебраических уравнений. Красноярск: изд-во СибГТУ, 2003. - 76 с.