Математика. 1. Дифференциальные и интегральные уравнения

Абдикаликова Г.А.

Актюбинский государственный университет им.К.Жубанова, Казахстан

Об исследовании одной краевой

задачи с нелокальным условием

Различные краевые задачи для уравнения с частными производными, в которых краевые условия представлены как соотношения между значениями искомых функций, вычисленные в различных точках, лежащих на границе или внутри рассматриваемой области исследованы многими авторами. Вопросу нахождения эффективных признаков однозначной разрешимости краевых задач с нелокальными условиями для различных классов уравнений с частными производными и дифференциально-операторных уравнений посвящено значительное количество работ, где разными методами получены достаточные условия существования единственного решения ,отметим лишь [1]-[2].

В работе [3] методом параметризации, исследованы вопросы однозначной разрешимости краевых задач для обыкновенных дифференциальных уравнений. В [4]-[5] методом введения функциональных параметров, являющимся модификацией метода параметризации на уравнения с частными производными, установлен критерий корректной разрешимости нелокальных краевых задач для системы гиперболических уравнений второго порядка.

Рассмотрим на , нелокальную краевую задачу

(1)

,, (2)

где --матрица,-вектор-функция непрерывны по всем аргументам на и непрерывно дифференцируемы по и ; --матрицы, - вектор-функция непрерывно дифференцируемы на .

Обозначим через пространство непрерывных по и на функций с нормой .

Целью работы является нахождение коэффициентных достаточных условий существования и единственности решения задачи (1)-(2).

Используя метод характеристик в области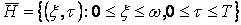 , 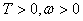получим семейство обыкновенных дифференциальных уравнений

,, (3)

, (4)

где ,,.

Если функция , непрерывная и непрерывно дифференцируемая по и в , является решением задачи (1)-(2),то будет решением (3)-(4), и наоборот, если функция из удовлетворяет уравнению (3) и условию (4), то учитывая функция , являющаяся непрерывной и дифференцируемой по и будет решением задачи (1)-(2) на .

К семейству линейных двухточечных краевых задач (3)-(4) применим метод параметризации [3].Возьмем шаг и производим разбиение . Обозначим через , сужение функции на . (3)-(4) приводится к эквивалентному семейству краевых задач:

,, , (5)

, (6)

,,, (7)

Здесь (7) является условием склеивания решения во внутренних линиях разбиения.

Решением задачи (5)-(7) является система функций , где каждая функция непрерывно дифференцируема по и ограничена на. Отметим, что в начальной точке интервала уравнению (5) удовлетворяет правосторонняя производная функции . Из непрерывности и ограниченности функции на интервале , и из [3] следует существование левосторонних пределов: . Значения и удовлетворяют (6),а значения и ,удовлетворяют соотношениям (7).

Если - решение задачи (3)-(4),то система его сужений будет решением задачи (5)-(7).

Через обозначим значение функции при.

На каждой области разбиения производим замену .

Получили краевую задачу с функциональными параметрами :

(8)

,, (9)

, (10)

,, . (11)

Если функция -решение задачи (3)-(4),то система пар функций

будет решением (8)-(11),и наоборот, если является решением (8)-(11),то функция,

которая получена при склеивании систем функций будет решением задачи (3)-(4).

В отличие от задачи (5)-(7) в задаче (8)-(11) появились начальные условия (9), которые позволяют определить из интегральных уравнений:

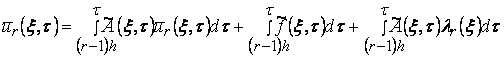. (12)

Подставляя в правую часть (12) и повторяя данный процесс раз, переходя к пределу при , используя краевые условия (10) и условия склеивания решения во внутренних линиях разбиения, умножая обе части (10) на ,имеем систему уравнений относительно параметров (:

(13)

где,,

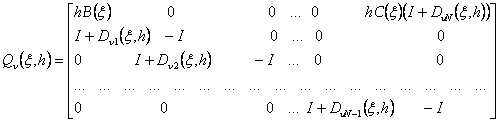-единичная матрица размерности ,

,

,

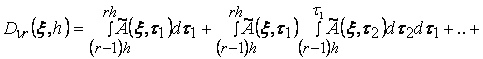
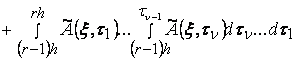. (14)

Одним из основных условий однозначной разрешимости исследуемой задачи является обратимость матрицы при некоторых : и,составленная по исходным данным задачи.

Для нахождения пар имеем замкнутую систему уравнений (12)-(13).Применяя метод последовательных приближений, ищем решение задачи (3)-(4).Для нахождения решения задачи с функциональными параметрами (8)-(11) – систему пар , - строим алгоритм. Достаточные условия сходимости алгоритма, а также вопрос о существовании единственного решения задачи (3)-(4) устанавливается теоремой.

Теорема 1. Пусть при некоторых и

- матрица обратима при всех и выполняются неравенства:

а)

б)

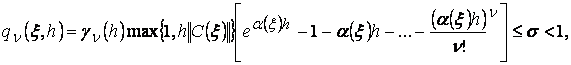
где

Тогда существует единственное решение задачи (3)-(4).

При доказательстве теоремы используется схема доказательства теоремы 1 [3,с.54].

Теорема 2. Пусть выполнены условия теоремы 1. Тогда задача (1)-(2) имеет единственное решение .

Из теоремы 1 следует, что задача (3)-(4) однозначно разрешима.

Так как краевая задача (3)-(4) эквивалентна задаче (1)-(2), то получим, что задача (1)-(2) имеет единственное решение .

Теорема 3. Краевая (3)-(4) однозначно разрешима тогда и только тогда, когда для любого ,существует , при котором матрица обратима и выполняются условия теоремы 1.

ЛИТЕРАТУРА

1.Пташник Б.И. Некорректные граничные задачи для дифференциальных уравнений с частными производными. Киев.1984. 264с.

2.Кигурадзе Т.И.,Кусано Т. //Дифферен. уравнения. 2003.Т. 39 ,№4.С.516-526.

3.Джумабаев Д.С. //Ж. вычисл.матем. и матем. физ.1989.Т.29,№1.С.50-66.

4.Асанова А.Т., Джумабаев Д.С //Известия МОН,НАН РК Сер.физ.-матем.2002.№3.С.20-26.

5. Асанова А.Т., Джумабаев Д.С // Дифферен. уравнения. 2003.Т.39,

№10.С.1343-1354.