Математика/1. Диференціальні і інтегральні рівняння

К. фіз.-мат. н. Чорний В. З., Цинайко П. В.,

Тернопільський національний педагогічний університет імені В. Гнатюка

Хома–Могильська С. Г.

Тернопільський національний економічний університет, Україна

Дослідження обернених задач для гіперболічних рівнянь другого порядку

Визначено коефіцієнти, для яких існує розв’язок таких двоточкових задач:

, , , (1)

, ; (2)

, , , (3)

, . (4)

Розглянемо функцію

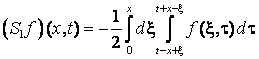. (5)

Відомо [1, 2], якщо , то функція є частинним розв’язком рівняння (1), оскільки

;;

;

.

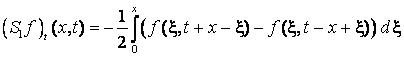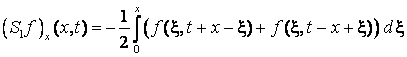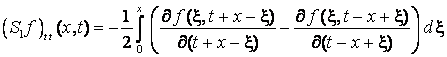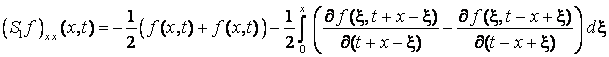Таким чином, .

Отже, функція є частинним розв’язком рівняння (1).

Введемо клас функцій .

Теорема 1. Якщо , то функція є частинним розв’язком двоточкової задачі (1), (2).

Доведення. Про те, що функція є частинним розв’язком рівняння (1), показано вище. Доведемо, що вона задовольняє крайові умови (2). Справді, при з (5) при маємо

, .

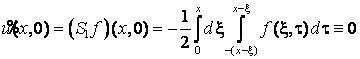Тепер, покладаючи у формулі (5), одержуємо

, ,

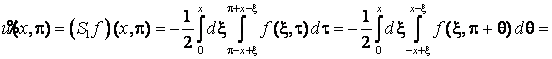
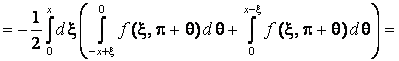
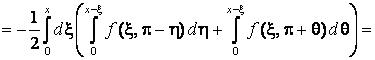
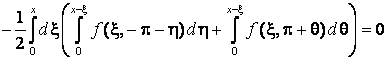що й потрібно було довести.

Справедливе твердження.

Теорема 2. Для кожної функції , , і функція

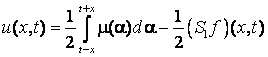(6)

є єдиним розв’язком двоточкової задачі (1), (2).

Тепер, на основі формули (6) можна встановити умови існування розв’язку двоточкової задачі (3), (4). Розглянемо інтегральне рівняння

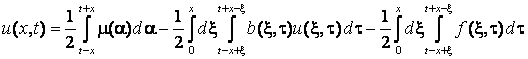. (7)

Якщо припустити, що коефіцієнти , і – неперервні в області , то методом послідовних наближень

;

, ,

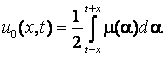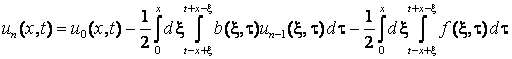легко довести, як це зроблено, наприклад, у роботі [3, с. 92-99], що інтегральне рівняння (7) має єдиний розв’язок, який задовольняє крайові умови (4) при умові, що , , , і або . Справді, при даних умовах

,

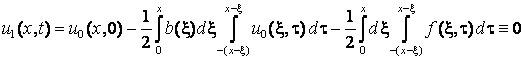, і всі наближення задовольняють двоточкові умови і , , а отже, гранична функція також задовольняє двоточкові умови (4).

Література:

1. Вейвода О., Штедры М. Существование классических периодических решений волнового уравнения: Связь теоретико-числового характера периода и геометрических свойств решений //Дифференц. уравнения. – 1984. – Т. 20, № 10.– С. 1733–1739.

2. Митропольский Ю. А., Хома Г. П., Громяк М. И. Асимптотические методы исследования квазиволновых уравнений гиперболического типа. – Киев: Наук. думка, 1991. – 232 с.

3. Петровский И. Г. Лекции об уравнениях с частными производными. М.: Физ-матгиз, 1961. – 400 с.