Секция: математика

подсекция: 4

Шаврова О.Б.

Дніпропетровський державний аграрний університет

ПЕРЕТВОРЕННЯ ТИПУ ЗГОРТКИ ДЛЯ ФУНКЦІЙ

З МОНОТОННИМИ КОЕФІЦІЄНТАМИ ФУР’Є

Нехай – простір вимірних – періодичних функцій , для яких існує інтеграл Лебега від функції з нормою 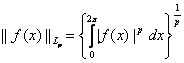. Для інтегральних перетворень типу згортки виду

,

де – будь-який дійсний параметр, а – задана функція обмеженої варіації на (міра множин на дійсній прямій, яка не дорівнює тотожньо нулю на і така, що ).

М.П.Тіман в роботі [1] при одержав оцінку величини

.

Ця оцінка має вигляд

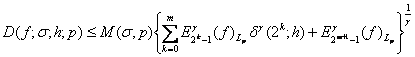, (1)

де,,, 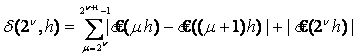– найкращі наближення функції тригонометричними поліномами в метриці простору .

В роботі [1] доведено, що (1) є точною за порядком оцінкою.

Нижче доводиться, що для кожної функції , у якої коефіцієнти Фур’є монотонно спадають оцінку (1) можна покращити.

Справедливо наступне твердження.

Теорема 1. Нехай функція має ряд Фур’є

,

у якої коефіцієнти Фур’є монотонно спадають. Тоді замість (1) справедлива оцінка

, (2)

де , .

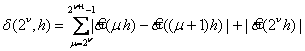Не обмежуючи загальність, проведемо доказ оцінки (2) лише для випадку, коли – функція парна та має ряд Фур’є виду .

Тоді

,

де .

Далі, завдяки нерівності Мінковського, маємо, що

.

Зауважимо, що коли оцінка (2) міститься в оцінці (1).

Для , завдяки відомої нерівності Пелі (див.[2], Т. II, § 5) , одержуємо, що

, (3)

де .

Для функцій з монотонно спадаючими коефіцієнтами Фур’є відомо (див.[3]), що

.

Тому, завдяки (3) одержимо, що

. (4)

Для оцінки скористуємось знову нерівністю Пелі для

.

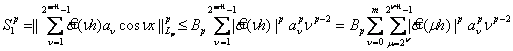Позначимо через

, , .

Тепер скористуємось тотожністю

.

Тоді

В зв’язку з тим, що коефіцієнтами Фур’є функції монотонно спадають, то завдяки результатам А. Конюшкова (див.[3]) ,

.

Тому

. (5)

Скористувавшись оцінкою (5), одержимо

. (6)

З оцінок (4) та (6) випливає твердження теореми 1.

Оцінка знизу величини міститься в наступному твердженні.

Теорема 2. Нехай функція задовольняє умовам теореми 1, тоді для справедлива оцінка

,

де константа не залежить від і функції .

Доведення оцінки (7) проводиться також за допомогою нерівності Пелі [2] для випадку та оцінки найкращих наближень функції через її коефіцієнти Фур’є.

Зауважимо, що вище були розглянуті лише парні функції. Для непарних, в яких ряд Фур’є має вигляд , завдяки тому, що у просторі , коли має місце нерівність М.Риса (див. [2], Т. I, с.404) оцінки вказані в теоремах 1 і 2 доводяться аналогічно.

Література:

1. Тиман М.Ф. Наилучшие приближения периодических функций тригонометрическими полиномами и преобразование типа свертки. – М.:ДАН СССР, 1971.-Т.198,№ 4.–С.776-779.

2. Зиґмунд А. Тригонометрические ряды. – М.: Мир, 1965. – Т. I, II.

3. Конюшков А.А. Наилучшие приближения тригонометрическими полиномами и коэффициенты Фурье. Матем.сб.1958 – Т.44,86:11.– С. 53-84.