рахимбеков А.Ж.

 Жетысуский Государственный университет  им. И. Жансугурова, Республика Казахстан

Метод концентрационной ЭДС на суперионике

          Разработаны и исследованы макеты кислородных насосов, предназначенных для получения кислорода особой чистоты электролитическим разделением воздуха на перегородке из твердого оксидного суперионного проводника (ТОСП) на основе диоксида циркония.

Твердый раствор диоксида циркония ZrO2 +12 мол. % CaO при Т = 10000С имеет удельную электропроводность σ =5,5·10-2 (Ом·см)-1 и сохраняет ионную долю электропроводности tu ≥0,99 вплоть до парциального давления кислорода P = 10-20 атм. При меньших давлений Р, часть кислорода покидает решетку, заряд компенсируется электронами, растет электронная составляющая проводимости, материал электролита деградирует «восстанавливается» [1].

          На электродах перегородки из такого материала, разделяющий объемы с Р' > Рх, существует электродвижущая сила (ЭДС) Е:

 

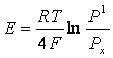                                                      ,                                            (1)

(здесь R- универсальная газовая постоянная, F – число Фарадея, Т-температура окружающей среды, -парциальное давление кислорода в окружающей атмосфере равное 0,21·105 Па, Рх –искомое давление кислорода). Это явление используют в топливных элементах, термодинамических исследованиях, газовом анализе.

Исследуемый материал выполняет роль твердого электролита. На его электродах с момента времени τ=0 поддерживается разность химических потенциалов кислорода . Стационарная ЭДС такой концентрации ячейки пропорциональна средней по электролиту ионной доле проводимости  

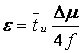                                                                          (2)

независимо от того, катионами или анионами она обусловлена.

          Действительно, если образец обладает смешанной проводимостью, обязанной анионам , катионам  и электронам с отличными от нуля концентрациями , зарядами и подвижностями в поле электрических сил

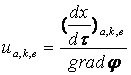
то, очевидно, под действием химических сил  анионы и катионы этого образца обнаружат отличную от нуля подвижность

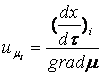
По аналогии с электрической проводимостью некоторого вида носителей

введем понятие об его «диффузионной проводимости»

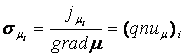
здесь - плотности потоков в А/м2, обусловленных движением i-го вида частиц в электрическом и кислородном концентрационном поле, соответственно [2].

Очевидно для электронов можно записать

                                                                                   (3)

Отношение этих проводимостей для анионов и катионов имеет вид

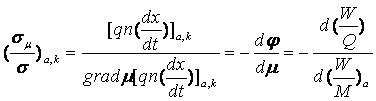                             (4)

где W-энергия, Q-количество электроэнергии, M-масса в молях. “Минус” обусловлен несовпадением знаков  и 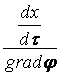 как для анионов, так и для катионов. Принимая распределение заряда в общей массе участвующих в проводимости анионов равномерным, перейдем к конечным приращениям и запишем

,

где 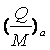 - заряд в кулонах, переносимый одним молем кислорода при z -ой степени его ионизации. Далее

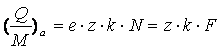
где е – заряд электрона, k – число атомов в молекуле, N – число Авогадро, F – число Фарадея. Поскольку для ионов 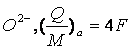, а выражение (4) равно справедливо для катионов и анионов, то можно записать

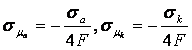                                                                     (5)

          Пусть образец не имеет макроскопических дефектов, по которым мог бы диффундировать молекулярный кислород. Тогда тенденция к самопроизвольному выравниванию , существующая в системе при , может реализоваться только посредством диффузии подвижных анионов и катионов. Рассмотрим их поведение в кислородном концентрационном поле.

Подвижные анионы образуют в электролите поток кислорода и, соответственно, отрицательного кислорода в сторону . На этом электроде выделяется кислород и возникает отрицательный заряд согласно реакции

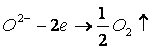                                                                      (6)

Со стороны  кислород входит в электролит, и электрод заряжается положительно согласно реакции

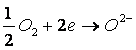                                                                         (7)

          Подвижные катионы образуют в электролите поток в сторону. Подошедшие к границе электролита избыточные катионы связывают соответствующее количество кислорода из среды с большей его концентрацией, образуя на этой границе новые слои электролита. Электрод на стороне заряжается положительно согласно реакции (7). Слой электролита со стороны  оказываются обедненным катионами. Избыточный кислород уходит из электролита и заряжает электрод отрицательно согласно реакции.

          В процессе диффузии нарастает разность электрических потенциалов ограничивающая диффузию.

Литература:

1.          А.Ж. Рахимбеков, Н.Е. Тимощенко «Входная характеристика кислородного насоса в области глубокой откачки», ЖТФ, т.54, стр.600, вып.3, 1984 г.

2.          A.B. Welch, Burzlaff, W. Cunningam, SPIE, 300, 15, 1981.