Физика / 1 Теоретическая физика.

Д. т. н. Иваницкий А.М., к. ф.-м. н. Дмитриева И.Ю.,

Рожновский М.В.

Одесская национальная академия связи им. А. С. Попова, Украина

Сведение «полной» системы дифференциальных уравнений Максвелла к шести скалярным уравнениям относительно компонент вектор-функции

В прикладных вопросах математики, физики, инженерии, как и ранее [1…3], существует проблема получения простым способом конструктивного решения системы дифференциальных уравнений в частных производных, поскольку все реальные физические процессы могут быть описаны именно таким образом. Но, так как спектр прикладных задач, математически смоделированных в виде систем указанного типа, достаточно обширен, на данном этапе исследований будем ограничиваться только вопросами классической электродинамики и, в частности, системой уравнений Максвелла в дифференциальной форме.

Так, в работе [4] Иваницким А.М. исследовалась проблема зависимости третьего и четвертого уравнений Максвелла от первых двух векторных уравнений, а в статье [5] этого же автора без применения только аналитических методов была доказана разрешимость системы дифференциальных максвелловских уравнений, основываясь на теории многомерных цепей.

В своей известной монографии [6] В.С. Владимиров строго обосновал существование решения максвелловской системы в частном случае пассивных систем. При этом был использован достаточно сложный аппарат теории обобщенных функций.

Заголовок работы [7] говорит сам за себя, и основные методы исследования здесь связаны с преобразованием Фурье и, опять-таки, теорией обобщенных функций. Применение обоих методов с конструктивной, прикладной точки зрения даже в случае систем линейных дифференциальных уравнений первого порядка, является задачей более чем трудоемкой, поскольку требует глубоких математических знаний по теории обобщенных функций и

интегральных преобразований.

Насколько известно, достаточно простого по применимости к конкретным инженерным и физическим задачам, конструктивного аналитического решения системы дифференциальных уравнений Максвелла, пока предложено не было.

Поэтому в работе [8] был рассмотрен достаточно простой метод сведения системы двух основных векторных уравнений Максвелла для однородных изотропных покоящихся сред к эквивалентной системе шести скалярных уравнений, каждое из которых содержит только одну компоненту векторов , либо Данный алгоритм базировался на последовательном применении соответствующих дифференциальных операторов к вышеупомянутой системе шести основных дифференциальных максвелловских уравнений в частных производных. Недостатками работы [8] можно считать то, что исследуемая система являлась «неполной», то есть в каждом из ее шести уравнений присутствовали не все компоненты искомых векторов и – скалярные функции а также недостаточную формализацию предложенного алгоритма.

Целью настоящей работы является исправление указанных упущений и дополнение результатов [8] обобщением предложенного там алгоритма на случай системы шести дифференциальных уравнений в частных производных, каждое из которых содержит уже все компоненты неизвестной вектор-функции , - скалярные функции а левые части уравнений рассматриваемой системы являются дифференциальными операторами вида

(1)

где:

и коэффициенты – произвольные известные действительные постоянные.

Скалярные функции предполагаются бесконечно-дифференцируемыми по всем четырем переменным.

Такую систему дифференциальных уравнений в частных производных для дальнейшей простоты изложения назовем «полной» максвелловской системой.

Рассмотрим данную систему дифференциальных уравнений

(2)

левая часть которой описана в (1), а правая – известные вектор-функции – бесконечно-дифференцируемые по всем четырем переменным.

Запишем систему (2) в следующем виде

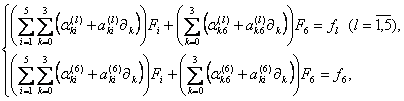(3)

то есть во всех уравнениях системы выделено слагаемое, содержащее компоненту , и последнее, шестое уравнение записано отдельно.

Применим к последнему, шестому уравнению в (3) оператор

(3')

а к первым пяти уравнениям – оператор

(3'')

и сложим почленно преобразованное шестое уравнение со всеми первыми пятью преобразованными уравнениями последовательно, при всех . В итоге придем к равносильной системе, первые пять уравнений которой уже не содержат компоненту :

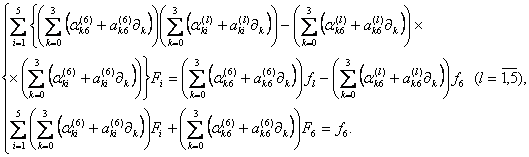
Применяя приведенный выше алгоритм последовательно пять раз и преобразовывая данную систему уравнений равносильным образом, после введения вспомогательных обозначений для известных дифференциальных операторов и функций, в результате получим систему (4) в которой все шесть уравнений – скалярные относительно искомых компонент вектора :

В (4) соответствующие известные дифференциальные операторы и функции имеют вид:

;

;

;

;

;

;

;

;

;

;

,

и система (4) эквивалентна исходной системе (2). Таким образом, полученный результат полностью соответствует цели, поставленной в данной работе.

Литература

1. Итоги науки и техники. Современные проблемы математики. Фундаментальные направления. Дифференциальные уравнения с частными производными.- М.: Наука, 1988. – Т.30. – 263 с.

2. Итоги науки и техники. Современные проблемы математики. Фундаментальные направления. Дифференциальные уравнения с частными производными.- М.: Наука, 1988. – Т.31. – 267 с.

3. Итоги науки и техники. Современные проблемы математики. Фундаментальные направления. Дифференциальные уравнения с частными производными.- М.: Наука, 1988. – Т.32. – 218 с.

4. Иваницкий А.М. Зависимость третьего и четвертого уравнений Максвелла от первых двух при произвольном возбуждении электромагнитного поля // Наукові праці ОНАЗ ім. О.С. Попова. – 2004. – №2. – С. 2 – 7.

5. Иваницкий А.М. Свойства дифференциальных операторов многомерных электрических цепей // Сб. научных трудов УГАС им. А.С. Попова. – Одеса, 1998. – с. 37 – 41.

6. Владимиров В.С. Обобщенные функции в математической физике. – М.: Наука, 1979. – 320 с..

7. Комеч А.М. Линейные уравнения в частных производных с постоянными коэффициентами. // Итоги науки и техники. Современные проблемы математики. Фундаментальные направления. – М.: Наука, 1988. – Т.31. – С. 127 - 261.

8. Иваницкий А.М., Дмитриева И.Ю., Рожновский М.В. Сведение классической системы уравнений Максвелла к скалярным уравнениям относительно компонент векторов и .// Наукові праці ОНАЗ ім. О.С. Попова. – 2006. – №1. – С. 37 – 47.

ФИО	Название	Адрес	Телефон	Секция	e-mail
Иваницкий А.М. Дмитриева И.Ю. Рожновский М.В.	Сведение «полной» системы дифференциальных уравнений Максвелла к шести скалярным уравнениям относительно компонент вектор-функции	Одесская национальная академия связи им. А.С. Попова, Украина, 65029, г. Одесса, ул. Кузнечная, 1.	8 048 20-78-67	Физика / 1 Теорети- ческая физика.	ivani@svitonline.com irina.dm@mail.ru Mixail_exp@list.ru