УДК 625.73

Главацкий К.Ц., Богомаз В.Н., Черкудинов В.Э., Проскурня В.Н.

Днепропетровский национальный университет

железнодорожного транспорта им. акад. В. Лазаряна

ЗАВИСИМОСТЬ УГЛА ПОВОРОТА ДЕБАЛАНСА

ГРУНТОУПЛОТНЯЮЩЕГО КАТКА ОТ ЕГО ПАРАМЕТРОВ

Для интенсификации работы катков грунтоуплотняющих машин с гладким вальцом целесообразно разместить внутри него виброконтур в виде комплекта дебалансов с зубчатым внутренним зацеплением и механизма их привода.

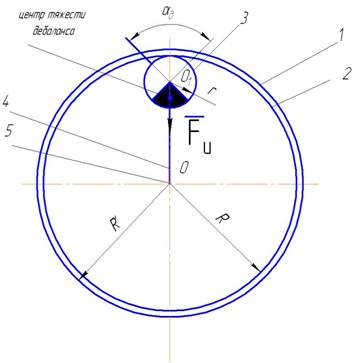
Элементарная часть виброконтура состоит из установленного внутри вальца 1 малого зубчатого колеса со смещенным центром тяжести 3, закрепленного на водиле 4, вращающемся вокруг продольной оси вальца 5. Колесо 3 находится в зацеплении с зубчатым венцом 2, жестко закрепленным на внутренней поверхности вальца 1 (рис. 1).

Рис. 1. Схема катка (1 – внешняя поверхность вальца; 2 – внутренняя поверхность вальца с зубчатым венцом; 3 – дебаланс с зубчатым зацеплением; 4 – водило; 5 – продольная ось вальца)

Задача состоит в определении угла поворота центра эксцентрика относительно вертикальной оси, проходящей через ось вращения малого зубчатого колеса, что позволит определить направление силы инерции. Для решения данной задачи зададимся некоторыми исходными данными: R – радиус делительной окружности зубчатого венца, м; r – радиус делительной окружности малого зубчатого колеса, м; R^’ – внешний радиус вальца, м; - угловая скорость вращения вальца, с^-1; - угловая скорость вращения водила вокруг оси вальца, с^-1.

Рассмотрим случаи вращения водила в сторону движения катка.

1. Каток движется с угловой скоростью , а водило неподвижно, т.е. , тогда угол поворота центра эксцентрика относительно вертикальной оси находится из зависимости:

, (1)

где - передаточное число в зубчатом зацеплении при вращении вальца; - момент времени, с.

Результат вычисления получим в градусах. Если , то необходимо от результата отнять целое число периодов вращения колеса. Например, , = 2 с^-1, = 2 с. Угол поворота центра тяжести дебаланса относительно вертикальной оси по формуле (1):

.

При возрастании времени и угловой скорости катка угол возрастает, т.е. эксцентрик вращается по направлению часовой стрелки и его направление вращения не меняется.

2. Когда , то угол поворота центра тяжести дебаланса относительно вертикальной оси находится из зависимости (2):

. (2)

Алгоритм получения результата в последующих случаях тот же, что и в предыдущем пункте.

При возрастании времени и угловой скорости катка угол возрастает, т.е. дебаланс вращается по направлению часовой стрелки и его направление вращения не меняется.

3. Когда , тогда угол поворота центра тяжести дебаланса относительно вертикальной оси находится из зависимости (3):

, (3)

где - передаточное число в зубчатом зацеплении при вращении водила.

В этом случае результат вычисления угла может оказаться отрицательным, тогда это означает, что дебаланс повернулся в направлении против движения катка относительно вертикальной прямой, проходящей через центр малого зубчатого колеса (против часовой стрелки).

4. Случай, когда , тогда угол поворота центра тяжести дебаланса относительно вертикальной оси находится из зависимости (4):

. (4)

При возрастании времени угол возрастает, т.е. дебаланс вращается по часовой стрелке.

Если же водило вращать в сторону, противоположную направлению движения катка, то угол поворота центра тяжести дебаланса относительно вертикальной оси по формуле (5):

. (5)

При возрастании времени и угловой скорости катка дебаланс вращается по часовой стрелке.

Выводы:

1. Предложен вариант интенсификации работы катка с гладким вальцом, заключающийся в использовании силы инерции, вращающегося по внутренней поверхности вальца малого зубчатого колеса со смещенным центром тяжести.

2. Предложена методика определения угла поворота центра тяжести дебаланса относительно вертикальной оси в любой момент времени в зависимости от угловых скоростей водила и вальца в целом, а также передаточных отношений U₁ и U₂ , что позволяет определить направление силы инерции от дебаланса.