Прикладная
математика и механика
Ромасько В.С. Харьковский государственный технический университет
строительства и архитектуры
О ВОЗМОЖНОСТИ ПРИМЕНЕНИЯ ТЕОРИИ
НЕРАВНОВЕСНЫХ ДЕФОРМАЦИОННЫХ ПРОЦЕССОВ ДЛЯ ОПИСАНИЯ НАДЕЖНОСТИ И ДОЛГОВЕЧНОСТИ
КОНСТРУКЦИИ, МАТЕРИАЛ КОТОРОЙ НАХОДИТСЯ В ХРУПКОМ СОСТОЯНИИ
1. Введение
В механике сплошных сред
сформировались два совершенно разных направления. Первое направление,
рассматривающее хрупкое состояние конструкций при температурах не превышающих
температуру вязкохрупкого перехода Т0, использует для описания свойств хрупкого
тела модель упругого тела с трещинами. Второе направление описывает с
использованием теории ползучести или модели
упруговязкопластического тела свойства материала и поведение конструкций
при температурах более высоких Т > Т0, чем температура Т0 вязкохрупкого
перехода. Модели и теории этих двух направлений взаимно не перекрываются,
поэтому исследование свойств материала, находящегося в упруговязкопластическом
состоянии при Т > Т0, ничего не дает для описания его же свойств в хрупком
состоянии, а исследование свойств материала, находящегося в хрупком состоянии,
ничего не дает для предсказания его упруговязкопластических свойств.
Трудности, обусловленные
существованием этих двух направлений, проявляются при решении задач
прогнозирования длительной прочности и ползучести матерала, при оценке
долговечности и надежности конструкции.
С появлением теории
неравновесных деформационных процессов появилась возможность объединить
указанные направления в одно, что позволит расширить возможности исследования
свойств материала, полнее использовать полученные результаты испытаний образцов
материала для оценки долговечности и надежности конструкции.
В данной работе
рассмотрены примеры использования теории неравновесных деформаионных процессов
для нахождения свойств огнепорного материала при температурах выше температуры
вязко-хрупкого перехода, которые затем используются для оценки долговечности и
надежности констукций из этого материала, находящихся в хрупком состоянии.
2. Скрытая роль скрытых параметров
Внутри модели упругого
тела с трещиной есть параметры, описывающие линейные свойства идеальной
кристаллической решетки, и геометрические характеристики длины и формы трещин,
рапределения их в пространстве, описывающие его нелинейные свойства. Все
остальные параметры явлются скрытыми для материала, находящегося в хрупком
состоянии. Внутри упруговязкопластических моделей материала важную роль играют
скрытые параметры, которые не входят в явном виде в определяющие соотношения,
но влияют на деформационный процесс. Примером служит скорость деформаци, не
входящая в деформационную теорию пластичности.
3. Сравнение теории пластического течения с деформационной
теорией пластичности
Сравнивая теорию
пластического течения с деформационной теорией пластичности [1], А.А. Ильюшин
уделил внимание условиям, в которых эти теории выполняются.
В теории
течения были приняты следующие допущения:
1. Объемная деформация ![]() связана с
гидростатическим давлением
связана с
гидростатическим давлением ![]() линейным законом
линейным законом ![]() . Здесь
. Здесь ![]() - модуль.
- модуль.
2. Девиатор напряжений пропорционален девиатору скоростей деформации. Коэффициент
пропорциональности зависит от интенсивностей напряжения и скорости деформации.
3. Для каждого материала
интенсивность напряжений ![]() является вполне
определенной функцией
является вполне
определенной функцией ![]() интенсивностей
деформаций
интенсивностей
деформаций ![]() и скоростей деформаций
и скоростей деформаций
![]() .
.
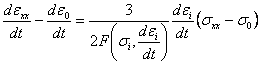 , (3.1)
, (3.1)
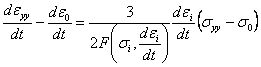 , (3.2)
, (3.2)
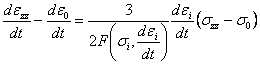 , (3.3)
, (3.3)
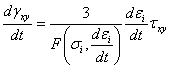 , (3.4)
, (3.4)
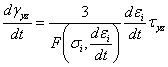 , (3.5)
, (3.5)
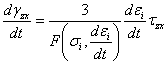 . (3.6)
. (3.6)
В деформационной теории пластичности
приняты следующие допущения:
1. Объемная деформация ![]() связана с
гидростатическим давлением
связана с
гидростатическим давлением ![]() линейным законом
линейным законом ![]() .
.
2. Девиатор напряжений пропорционален
девиатору деформаций. Коэффициент пропорциональности зависит от интенсивностей
напряжения и деформации.
3. Для каждого материала
интенсивность напряжений является вполне определенной функцией интенсивности
деформаций ![]()
![]() , (3.7)
, (3.7)
![]() , (3.8)
, (3.8)
![]() , (3.9)
, (3.9)
![]() , (3.10)
, (3.10)
![]() , (3.11)
, (3.11)
![]() . (3.12)
. (3.12)
Соотношения (3.7-12) позволяют построить тензор подобия ![]() с компонентами
с компонентами
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
которые, по мнению А.А. Ильюшина, не должны зависеть от времени. Они и не
зависят, если деформационная теория пластичности формулируется для бесконечно
медленного (статического) изменения нагрузки.
,
которые, по мнению А.А. Ильюшина, не должны зависеть от времени. Они и не
зависят, если деформационная теория пластичности формулируется для бесконечно
медленного (статического) изменения нагрузки.
Вместо
того, чтобы ограничиться рассмотрением равновесных деформационных процессов,
для которых компоненты тензора подобия не зависят от времени, А.А. Ильюшин сформулировал
другое условие, при выполнении которого деформационная теория пластичности согласуется с теорией
течения. Он потребовал, чтобы нагрузки изменялись пропорционально одному
параметру. Такой неравновесный режим изменения нагрузок, при котором кривизна
траектории деформации характеризуется бесконечно большим радиусом кривизны и,
соответсвенно, бесконечно малой кривизной, был назван простым. К сожалению, в
этом условии допущена ошибка, состоящая в том, что все материалы при
равновесных напряжениях не текут, следовательно, при напряжениях равных
равновесным напряжениям уравнения состояния (3.7-12) деформационной теории
справедливы, а уравнения течения (3.1-6) не выполняются.
4. Определяющие уравнения теории неравновесных деформационных
процессов
Теория неравновесных
деформационных процессов построена с целью уменьшения числа скрытых параметров,
за счет включения деформации, не совпадающей по фазе с напряжениями, и их
скорости, равновесных (на мезоуровне) и полных напряжений (на макроуровне),
температуру в определящие соотношения.
Для равновесных
деформационных процессов уравнения состояния были получены ранее [2]. Если
уравнения состояния сформулировать в терминах не вполне упругих деформаций ![]() и равновесных напряжений
и равновесных напряжений ![]()
![]() , (4.13)
, (4.13)
![]() , (4.14)
, (4.14)
![]() , (4.15)
, (4.15)
![]() , (4.16)
, (4.16)
![]() , (4.17)
, (4.17)
![]() , (4.18)
, (4.18)
а кинетические
уравнения представить так [3]
![]() (4.19)
(4.19)
![]() (4.20)
(4.20)
![]() (4.21)
(4.21)
![]() (4.22)
(4.22)
![]() (4.23)
(4.23)
![]() (4.24)
(4.24)
![]() (4.25)
(4.25)
то оказывается, что нет необходимости их
согласовывать между собой, так как равновесные напряжения содержатся в уравнении
кинетики (4.19-24) в явном виде. Здесь предполагается, что полная деформация
является суммой упругих деформаций, изменяющихся в фазе с напряжениями, и не
вполне упругих деформаций, запаздывающих относительно напряжений.
Уравнения
состояния (4.13-18) и кинетики (4.19-24) дополняют друг друга. Кинетическое
уравнение (4.25) для объемной не вполне упругой деформации ![]() содержит объемную
вязкость
содержит объемную
вязкость ![]() , величина которой меньше коэффициента сдвиговой вязкости
, величина которой меньше коэффициента сдвиговой вязкости ![]() , поэтому кинетический процесс, описываемый уравнением (4.25),
завершается раньше, чем кинетический процесс, описываемый уравнениями (4.19-24).
, поэтому кинетический процесс, описываемый уравнением (4.25),
завершается раньше, чем кинетический процесс, описываемый уравнениями (4.19-24).
Теория
неравновесных деформационных процессов, содержащая в явном скрытые параметры,
позволяет сначала экспериментально определить параметры материала, находящегося
в упруговязкопластическом состоянии, а затем использовать эти параметры для
описания долговечности и вероятности отказа конструкции, материал которой
находится в хрупком состоянии.
Полная
система уравнений (4.13-25) справедлива для любых материалов, находящихся при
температурах как выше ![]() , так и ниже
, так и ниже ![]() температуры
температуры ![]() вязко - хрупкого
перехода. Утверждение о том, что теория неравновесных деформационных процессов
применима для описания поведения конструкций, материал которых находится при
температурах выше
вязко - хрупкого
перехода. Утверждение о том, что теория неравновесных деформационных процессов
применима для описания поведения конструкций, материал которых находится при
температурах выше ![]() температуры
температуры ![]() вязко - хрупкого
перехода вызывает меньше возражений, чем допущение о возможности ее применения
при температурах ниже
вязко - хрупкого
перехода вызывает меньше возражений, чем допущение о возможности ее применения
при температурах ниже ![]() температуры
температуры ![]() вязко - хрупкого
перехода, где разрушение происходит внезапно без видимых проявлений временных
эффектов. Это объясняется тем, что теория пластичности развита, несмотря на ее
критику, значительно лучше, чем теория, описывающая поведение материала, в
хрупком состоянии, которая основывается на модели идеального упругого тела с
трещиной. Модель идеального упругого тела с трещиной, использующая
энергетический критерий роста трещины Гриффитса, не позволяет оценить
долговечность и вероятность разрушения конструкции, так как модель упругого
тела не учитывает временные эффекты [4], происходящие при неравновесных деформационных
процессах. Хрупкое разрушение конструкции представляет собой гораздо менее
воспроизводимое явление, чем ее разрушение, которому предшествует значительная
пластическая деформация. Результаты испытаний идентичных образцов, находящихся
в хрупком состоянии колеблются от одной трети до утроенной величины среднего
значения [5].
вязко - хрупкого
перехода, где разрушение происходит внезапно без видимых проявлений временных
эффектов. Это объясняется тем, что теория пластичности развита, несмотря на ее
критику, значительно лучше, чем теория, описывающая поведение материала, в
хрупком состоянии, которая основывается на модели идеального упругого тела с
трещиной. Модель идеального упругого тела с трещиной, использующая
энергетический критерий роста трещины Гриффитса, не позволяет оценить
долговечность и вероятность разрушения конструкции, так как модель упругого
тела не учитывает временные эффекты [4], происходящие при неравновесных деформационных
процессах. Хрупкое разрушение конструкции представляет собой гораздо менее
воспроизводимое явление, чем ее разрушение, которому предшествует значительная
пластическая деформация. Результаты испытаний идентичных образцов, находящихся
в хрупком состоянии колеблются от одной трети до утроенной величины среднего
значения [5].
5.Уравнение состояния для материала, находящегося в хрупком состоянии
Для
описания равнвесной деформационной кривой в опытах на сжатие удобно
использовать степенную функцию
![]() , (5.1)
, (5.1)
параметрами которой служат показатель степени ![]() и множитель А,
являющиеся функциями температуры.
и множитель А,
являющиеся функциями температуры.
6. Гипотеза о предельном
состоянии материала на мезоуровне
Предполагается,
что на мезоуровне сужествуют предельные равновесные напряжения ![]() и деформации
и деформации ![]() , при достижении которых происходит разрушение его элементов
структуры.
, при достижении которых происходит разрушение его элементов
структуры.
7. Влияние температуры
на равновесные напряжения ![]() и деформации
и деформации ![]() в предельном состоянии
на мезоуровне хрупкого материала
в предельном состоянии
на мезоуровне хрупкого материала
Влияние температуры на равновесные
напряжения ![]() и деформации
и деформации ![]() в предельном состоянии
на мезоуровне хрупкого материала можно описать в явном виде с использованием
функций
в предельном состоянии
на мезоуровне хрупкого материала можно описать в явном виде с использованием
функций
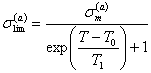 , (7.1)
, (7.1)
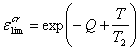 . (7.2)
. (7.2)
Экспериментально определяемые
параметры функций (7.1) и (7.2) характеризуют величину хрупкой прочности ![]() , температуры
, температуры ![]() ,
, ![]() ,
, ![]() и показатель степени
и показатель степени ![]() .
.
8. Влияние температуры
на рановесную деформационную кривую хрупкого материала
Для описания в
явном виде температурного влияния на параметры равновесной деформационной
кривой, описывающей сопротивление деформации на мезоуровне, используются
следующие функции
![]() , (8.1)
, (8.1)
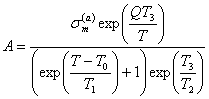 . (8.2)
. (8.2)
9. Явная температурная
зависимость параметров кинетического уравнения в форме обобщенного уравнения
Ребиндера
Обобщенное
уравнение Ребиндера [1]
![]() , (9.1)
, (9.1)
не содержащее температуру в явном
виде, с учетом функций (8.1), (8.2), описывающих в явном виде влияние
температуры на величины параметров уравнения состояния (5.1), позволяет
определить в явном виде связь между скоростью деформации ![]() , напряжениями
, напряжениями ![]() , деформациями
, деформациями ![]() и температурой
и температурой ![]() , которую, введя переменную
, которую, введя переменную ![]() , можно представить так:
, можно представить так:
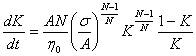 . (9.1)
. (9.1)
10. Оценка долговечности конструкции
Интегрируя
дифференциальное уравнение (9.1) с разделяюшимися переменными можно получить зависимость времени ![]() до достижения
предельной деформации на мезоуровне
до достижения
предельной деформации на мезоуровне ![]() , при заданных величинах напряжения
, при заданных величинах напряжения ![]() и температуры
и температуры ![]() .
.
11. Влияние напряжения на плотность распределения элементов структуры на
мезоуровне при заданной температуре
Плотность распределения ![]() элементов структуры на
мезоуровне можно получить в аналитическом виде
элементов структуры на
мезоуровне можно получить в аналитическом виде
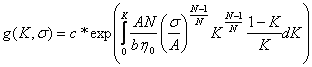 (11.1)
(11.1)
по формуле Понтрягина с использованием
кинетического уравнения (9.1). Здесь ![]() - нормировочный
параметр,
- нормировочный
параметр, ![]() - подгоночный параметр, характеризующий среднеквадратическое
отклонение от среднего
- подгоночный параметр, характеризующий среднеквадратическое
отклонение от среднего ![]() в стохастическом
деформационном процессе.
в стохастическом
деформационном процессе.
12. Пример построения
кривых долговечности для динаса, используемого в обогревательных простенках
коксовых печей.
Одна
из трудностей проектирования коксовых батарей состоит в том, что материалом, из
которого изготовлена кладка обогревательных простенков печей служит динас,
находящийся в хрупком состоянии даже при сравнительно высоких температурах.
Динас эксплуатируется при температурах, не превышающих 1473К, которым
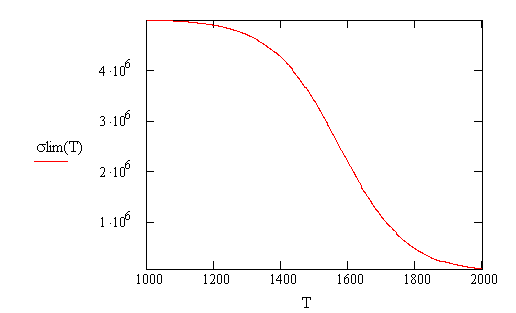
соответствуют большие величины предельных величин равновесных напряжений и малые
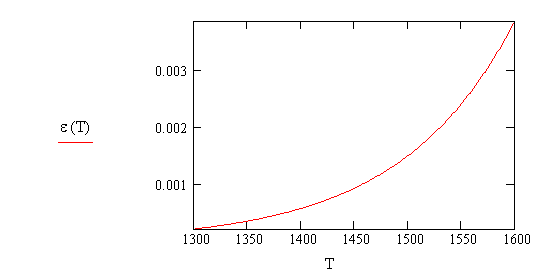
величины деформаций рис.1, 2.
 (а)
(а)
 (б)
(б)
Рис.1. Температурные зависимости предельных величин равновесных
напряжений и деформаций на мезоуровне,
вычисленные по формулам (7.1) при значениях хрупкой прочности элементов
структура на мезоуровне равной ![]() Па и температрных параметров
Па и температрных параметров ![]() =1573К,
=1573К, ![]() =100К и деформации на
мезоуровне, расчитанная по формуе (7.2)
при
=100К и деформации на
мезоуровне, расчитанная по формуе (7.2)
при ![]() 20.587,
20.587, ![]() =106.445K. Здесь на рис.1(а)
=106.445K. Здесь на рис.1(а) ![]() обозначает
обозначает ![]() , а на рис.1(б)
, а на рис.1(б) ![]() обозначает
обозначает![]() .
.
При значении
температурного параметра ![]() равного 2921К величина
показателя степени
равного 2921К величина
показателя степени ![]() , вычисленная по формуле (8.1), оказывается близка к 2.
Влияние деформации на мезоуровне и напряжения на макроуровне на долговечность
динасовой кладки можно оценить с помощью формулы,
, вычисленная по формуле (8.1), оказывается близка к 2.
Влияние деформации на мезоуровне и напряжения на макроуровне на долговечность
динасовой кладки можно оценить с помощью формулы,
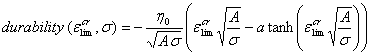 , (12.1)
, (12.1)
полученной
интегрированием (9.1) при началтном условии ![]() для текущего
для текущего ![]() и предельного
и предельного ![]() значений при
значений при ![]() величины
величины ![]()
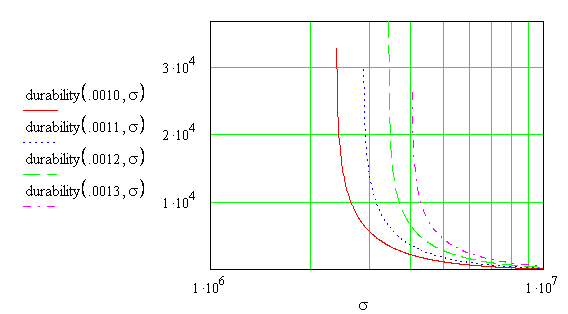
Рис.3. Зависимости долговечности динасовой кладки от
напряжения на макроуровне (Па), для четырех значений 0.0010, 0.0011, 0.0012,
0.0013 предельной деформации на мезоуровне, вычисленные по формуле (12.1).
На
рис.3 видно, что при напряжениях, не превышающих 2МПа, долговечность динасовой
кладки равна бесконечности, однако, с ростом напряжения долговечность быстро
убывает. Этот результат объясняет неожиданные разрушения обогревательных
простенков коксовых печей, происходящие не сразу после начала эксплуатации
коксовой батареи, а спустя двенадцать лет после ее пуска.
13. Оценка вероятности отказа динасовой кладки
Функция![]() плотности распределения элементов структуры динаса по
отношениям равновесных напряжений на мезоуровне к напряжению на макроуровне,
полученная по формуле (11.1) при
плотности распределения элементов структуры динаса по
отношениям равновесных напряжений на мезоуровне к напряжению на макроуровне,
полученная по формуле (11.1) при ![]()
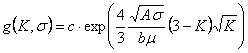 (13.1)
(13.1)
позволяет оценить вероятность 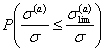 события, состоящего в
том, текущая величина
события, состоящего в
том, текущая величина ![]() не превышает
пределного значения
не превышает
пределного значения ![]()
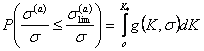 . (13.2)
. (13.2)
Вероятности отказа конструкции можно оценить как вероятность 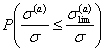 события, состоящего в
том, текущая величина
события, состоящего в
том, текущая величина ![]() превышает пределное
значения
превышает пределное
значения ![]()
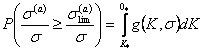 (13.3)
(13.3)
Действительно, при напряжении ![]() МПа,
МПа, ![]() =1 МПа,
=1 МПа, ![]() =20 МПа функции плотностей (13.1) на рис.4(а,б,в), которым
соответствуют значения нормировочной постоянной с=0.056, с=0.143, с=0.149,
позволяют оценить вероятность события.
=20 МПа функции плотностей (13.1) на рис.4(а,б,в), которым
соответствуют значения нормировочной постоянной с=0.056, с=0.143, с=0.149,
позволяют оценить вероятность события.
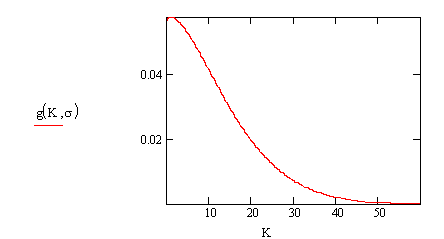 (а)
(а)
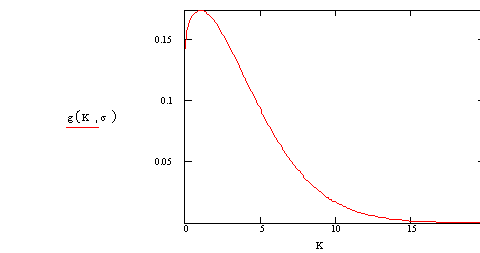 (б)
(б)
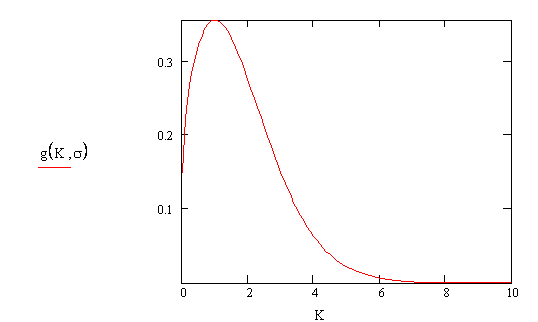
(в)
Рис.4(а,б,в) Плотности распределения элементов структуры на
мезоуровне по К при различных напряжениях на макроуровне, построенные для
напряжений а - ![]() =0.02 МПа, б -
=0.02 МПа, б - ![]() =1МПа, в -
=1МПа, в - ![]() =20МПа, которым соответствуют значения нормировочных
постоянных с=0.056, с=0.143, с=0.149 и вероятности отказов
=20МПа, которым соответствуют значения нормировочных
постоянных с=0.056, с=0.143, с=0.149 и вероятности отказов ![]() ,
, ![]() ,
, ![]() .
.
Таким образом, с ростом напряжения
вероятность отказа конструкции, вычисенная по формуле (13.3) растет, что
согласуется с кривой долговечности на рис.3.
Литература
1. Ильюшин А.А. Связь между теорией Сен Венана – Леви – Мизеса и теорией малых упруго-пластических деформаций. //Прикладная математика и механика. 1945. -Т.9.-С.207-217.
2. Ромасько В.С., Баранник В. Уравнение
состояния твердого деформируемого тела
при равновесном термомеханическом взаимодействии с внешними телами //
Науковий вісник будівництва.
Харків: ХДТУБА.-2005.-№28.-С.251-256.
3. Ромасько В.С. Уравнения ползучести и
релаксации напряжения при сложном напряженном состоянии.// Науковий вісник будівництва.
Харків: ХДТУБА.-2005.-№28.-С.116-125.
4. Вавакин А.С., Викторов В.В., Мохель
А.Н., Степанов Л.П. Временные эффекты при пластическом деформировании металлов.
// Пластичность и разрушение твердых тел. Сборник научных трудов из серии
«Прочность и вязкоупругопластичность» М.: Наука. 1988.-С.29-40.
5. Фрейденталь А.М. Статистический
подход к хрупкому разрушению. / Перевод с английского в семи томах. Разрушение.
// Под ред. Вавакина А.С. Математические основы теории разрушения Т.2 - М.:
Мир. Т2.-С.616-645
6.
Ромасько
В.С. Дослідження
впливу рівнів напруження та температури на роподіл міцності у тілі, що
знаходиться у крихкому, або пластичному стані. // Доповіді НАН України.
1997.-№12.-С.71-75.