Технические науки/12 Автоматизированные системы управления на производстве.

К.т.н. Тараненко Ю.К.

Днепропетровский университет экономики и права

Автоколебательная система виброчастотных датчиков с нелинейным механическим резонатором

Границей достижимой точности измерения физических величин является точность воспроизведения эталонов этих величин. Так погрешность воспроизведения эталонов аналоговых величин: силы электрического тока - ; электрического сопротивления ; частоты колебаний [1].. Это позволяет сделать вывод о том, что на современном этапе развитии приборостроения точность частотных измерительных систем значительно выше точности других аналоговых измерительных систем.

При автоматизации производственных процессов места измерения и контроля технологических параметров удалены от мест централизованной обработки измерительной информации, которая осуществляется с применением вычислительной техники. Поэтому при создании автоматизированных систем управления технологическими процессами (АСУ ТП) возникают три проблемы, первая – необратимые потери измерительной информации при её передачи по каналам связи, вторая – потери информации при коммутации сигналов от датчиков технологических параметров, третья –потери информации при преобразование сигналов в код, для их дальнейшей обработки с применением вычислительной техники. В этой связи частотно - модулирований сигнал является наиболее помехазащищённым, а коммутаторы частотных сигналов не вносят дополнительных погрешностей в результаты измерений, а их техническая реализация значительно проще, чем аналоговых. Частотный сигнал может быть преобразован в код практически без потери точности.

Для преобразования технологического параметра в частоту используются частотные датчики, среди которых лучшие метрологические характеристики имеют датчики резонаторами образующие колебательные системы с распределенными механическими параметрами — массой, жесткостью, демпфированием [2].. Такие датчики строятся на основе автогенератора, частотно задающим элементом, которого является механический резонатор. Резонатор это цилиндр, струна, пластина, камертон, которые образуют механические колебательные системы с распределёнными механическими параметрами [3].. В механических колебательных системах проявляется нелинейность, которая обусловлена отклонением упругих свойств материала резонатора от закона Гука. Вследствие этого явления эквивалентная жёсткость и масса резонатора становятся периодическими функциями, и провоцирую появление параметрического резонанса с отклонением формы колебаний от синусоидальной. Это увеличивает погрешность измерения. Нелинейность реального механического резонатора имеет два следующих случая проявления в автогенераторах:

· Частота автоколебаний уменьшается, при увеличении их амплитуды, такую нелинейность принято называть нелинейностью “мягкого” типа;

· Частота автоколебаний увеличивается, при увеличении их амплитуды, такую нелинейность принято называть нелинейностью “жёсткого” типа;

На практике проявление нелинейных свойств механических резонаторов может иметь и более сложный характер, например при малых амплитудах проявляется нелинейность “мягкого” типа, которая с ростом амплитуды переходит в нелинейность “жёсткого” типа.

Исследование обеих типов нелинейности можно проводить с использованием структурной схемы системы возбуждения колебаний механического резонатора приведенной на рисунке.

Где 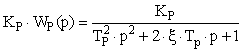— передаточная функция линейной части резонатора; - функция нелинейной части резонатора; — оператор дифференцирования, который для гармонических колебаний равняется ;

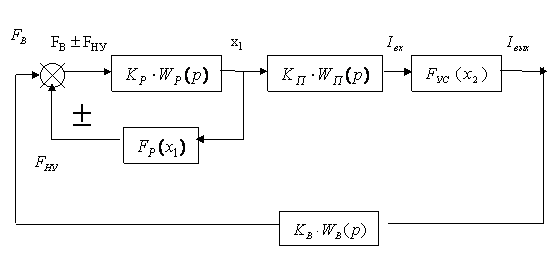
Рисунок. Структурная схема возбуждения колебаний механического резонатора.

- сила создаваемая возбудителем колебаний; – нелинейная составляющая силы упругости резонатора; — механическое перемещение резонатора; - ток или напряжение на выходе приёмника колебаний резонатора (в зависимости от типа приёмника колебаний); — ток или напряжение на выходе усилителя.

— квадрат круговой частоты собственных колебаний резонатора; — нормированный, приведенный коэффициент затухания колебаний резонатора; , — период собственных колебаний резонатора; — статический коэффициент передачи резонатора; — передаточная функция приёмника колебаний резонатора; — статический коэффициент приёмника колебаний резонатора; — передаточная функция возбудителя колебаний резонатора, как без инерционного звена; — статический коэффициент передачи возбудителя колебаний резонатора, который зависит от выбранной системы возбуждения колебаний; — функция преобразования усилителя; , — координаты системы; — знак обратной связи для “мягкого” типа нелинейности; — знак обратной связи для “жёсткого” типа не линейности.

Автоколебательная система виброчастотных датчиков приведенная на рисунке была исследована модифицированным методом гармонической линеаризации [4,5].. Автором были получены следующие соотношения для частоты автоколебаний.

Для механического резонатора с нелинейностью “мягкого” типа:

а) Положительная обратная связь с не инвертирующим нелинейным усилителем:

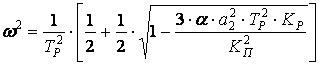(1)

При выполнении условий:

(2)

б) Отрицательная обратная связь с инвертирующим нелинейным усилителем:

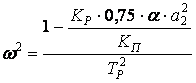(3)

Для механического резонатора с нелинейностью “жёсткого” типа:

а) Положительная обратная связь с не инвертирующим нелинейным усилителем:

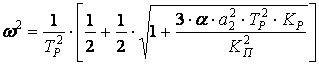(4)

При выполнении условий:

б) Отрицательная обратная связь с инвертирующим линейным усилителем:

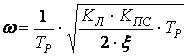(5)

При выполнении условий:

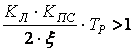(6)

в) Отрицательная обратная связь с инвертирующим нелинейным усилителем:

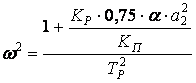(7)

Полученные соотношения использовались при проектировании виброчастотных плотномеров жидких сред (светлых нефтепродуктов), что позволило за счёт выбора оптимальной структуры автогенератора снизить абсолютную погрешность измерения плотности на 15÷20 %.

Литература:

1. Эткин Л.Г. Виброчастотные датчики. Теория и практика. — М.:Изд-во МГТУ им. Н.Э. Баумана, 2004.— 408 с.

2. Новицкий П.В.,Кнорринг В.Г.,Гутников В.С. Цифровые приборы с частотными датчиками. Л.: Энергия, 1970, 423 с.

3. Диференційний віброчастотний метод вимірювання щільності газів, рідин та дисперсних систем /Ю.К.Тараненко//Вопр. химии и хим. технологии . — 2006. — № 3 с.201-203

4. Цыпкин Я.З. Релейные автоматические системы.— М.: Физматгиз, 1974 г. 575 с.

5. Попов Е.П., Пальтов И.П. Приближённые методы исследования нелинейных систем. ИФМЛ. М.:1960 — 498 с.