Технічні науки/Металургія
Ісаєнко
О.М., Качан Ю.Г., Іванов В.І.,
Болюк С.В., Моісейко Ю.В.
МОДЕЛЬ СЕГРЕГАЦІЇ РУДИ В БУНКЕРІ У РАЗІ ЙОГО «ТОЧКОВОГО» ЗАВАНТАЖЕННЯ
Запорізька державна
інженерна академія,
Національна металургійна академія України
Явище сегрегації є основним чинником, що порушує
стабільну роботу усереднювальних пристроїв з донним випусканням руди. У масі
сипкого матеріалу, що завантажують до бункера, виникають неоднорідності за
розмірами частинок, які під час подальшого розвантаження формують коливання
гранулометричного складу руди на виході усереднювального пристрою. Успішне
розв’язання завдання максимально можливого зниження впливу сегрегації на якість
руди, що розвантажують, є неможливим без знання закономірностей розділення
частинок руди за розмірами під час завантаження бункерів і формування штабелів.
Авторами проведено математичне моделювання процесу
сегрегації руди для «точкового» завантаження бункера на конус. Розглядали течію
незв'язного сипкого твердого тіла постійної глибини Н шорсткою бічною поверхнею
конуса кінцевої довжини L (L >> H).
Швидкість руху шару матеріалу ухилом ![]() визначали з матеріального балансу процесу:
визначали з матеріального балансу процесу:
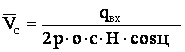 , (1)
, (1)
де qвх
- продуктивність джерела живлення; r -
відстань від точки завантаження ![]() ;
; ![]() , j - насипна щільність і кут природного ухилу матеріалу
відповідно.
, j - насипна щільність і кут природного ухилу матеріалу
відповідно.
Приймали, що розподіл радіальних швидкостей частинок за
висотою потоку руди має вигляд степеневої залежності:
 ,
(2)
,
(2)
де ![]() - відстань від основи потоку уздовж нормалі до
бічної поверхні конуса
- відстань від основи потоку уздовж нормалі до
бічної поверхні конуса ![]() .
.
У поперечному перерізі потоку враховували три
середньостатистичні сили: силу опору руху ![]() , градієнтну силу
, градієнтну силу ![]() та силу сегрегації
та силу сегрегації ![]() :
:
![]() ;
; 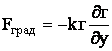 ;
; ![]() , (3)
, (3)
де ![]() - коефіцієнт опору руху; k - коефіцієнт дифузії;
ks - коефіцієнт сегрегації;
- коефіцієнт опору руху; k - коефіцієнт дифузії;
ks - коефіцієнт сегрегації;
![]() -
диференціальна функція розподілу розмірів частинок руди.
-
диференціальна функція розподілу розмірів частинок руди.
Нормальну складову вектора швидкості частинок вузького
класу визначали з рівняння балансу вказаних сил з урахуванням формул (3):
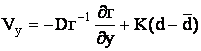 , (4)
, (4)
де D - коефіцієнт макродифузії; k - приведений
коефіцієнт сегрегації.
Рівняння нерозривності для елемента шару бічної поверхні
конуса:
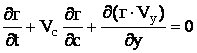 , (5)
, (5)
де ![]() - диференціальна функція розподілу розмірів
частинок руди в точці (r,y) потоку на момент часу t; dr - радіальний приріст елемента шару.
- диференціальна функція розподілу розмірів
частинок руди в точці (r,y) потоку на момент часу t; dr - радіальний приріст елемента шару.
Після підставляння формул (1), (2) і (4) до рівняння (5)
одержували:
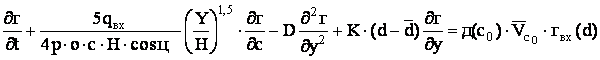 , (6)
, (6)
де ![]() - дельта-функція;
- дельта-функція; ![]() - радіальна швидкість потоку в точці
- радіальна швидкість потоку в точці ![]() джерела живлення шару;
джерела живлення шару; ![]() - гранулометричний склад руди, що
завантажують.
- гранулометричний склад руди, що
завантажують.
Краєві умови процесу, що досліджують, задавали як:
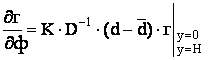 , (7)
, (7)
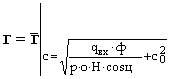 ,
,
де
 .
.
![]() .
(8)
.
(8)
Розв’язання рівняння (6) одержали методом кінцевих
різниць з використанням явної різницевої схеми на сітці з постійним кроком за
координатами Dr,Dy та змінним кроком за часом Dt.
Результати моделювання процесу розділення частинок по
крупині показали, що розрахункова залежність середнього розміру частинок від
відстані до вершини конуса має чотири ділянки. На першій ділянці масова частка
окремих фракцій руди подана в пропорції початкового живлення. Зменшення
середнього розміру частинок на другій ділянці відбувається за рахунок
накопичення частинок дрібних фракцій руди, які осідають на основу потоку. Третя
ділянка характеризується зменшенням частки дрібних фракцій і збільшенням частки
значних фракцій. На четвертій ділянці спостерігали накопичення частинок значних
фракцій при відносно малій частці дрібних фракцій, внаслідок чого середній
розмір частинок на цій ділянці поверхні конуса значно зростає порівняно із
середнім розміром частинок початкового живлення.
Достатній збіг практичних даних з результатами
моделювання підтверджує, що домінуючим механізмом сортування частинок за
розмірами у потоці руди, що завантажується, є дія сил відштовхування, які
виникають як результат зіткнення частинок між собою, а також градієнта
швидкостей частинок за висотою потоку.