Технічні науки / механіка

ас. Проскурня В.М., к.т.н. Бондаренко Л.М., ас. Дідковський Л.В.

Дніпропетровський національний університет залізничного транспорту ім. ак. В.А. Лазаряна (ДІІТ)

Про одну складову опору кочення кулі

Постановка проблеми і зв'язок з науковими завданнями. При розрахунках опору руху кулі по основі любої конфігурації використовують коефіцієнт тертя кочення, як похідну від півширини плями контакту [1, 2]. Звичайно, що таке рішення визначає тільки «чисте» кочення. Але при коченні виникають і опори від проковзування кулі в місці контакту. Цей опір виникає тільки при контакті тіл з різними пружними константами. Вважається також, що мікро проковзування виникає також і внаслідок різної кривизни двох тіл.

Але в місці контакту кривизна обох контактуючих тіл однакова, тому останнє ствердження необхідно поставити під сумнів. Справа у тому, що радіус кочення, наприклад кулі по площині, є змінним на довжині плями контакту і мікро проковзування будуть виникати із-за цього. Тому необхідно встановити, яку частину опору кочення кулі складає ця складова від чистого.

Аналіз останніх досліджень і публікацій.

Проблеми визначення мікро проковзування на контакті кочення двох тіл, якісно розглянуті Рейнольдом [3], а кількісно вони розглянуті майже через 100 років Табором [2], експериментально.

Табором були отримані аналітичні залежності для визначення коефіцієнта тертя кочення, але наявність в них коефіцієнта гістерезисних витрат не дозволяє використовувати їх в інженерній практиці. Звичайно, що у цьому випадку неможливо виділити із експериментальної величини опору кочення складову, яка припадає на чисте кочення.

Невирішені частини проблеми. Внаслідок різної величини радіуса кочення кулі виникають мікропроковзування. Але невідомо яку частку вони складають від загального.

Метою статті є встановити приведений коефіцієнт тертя кочення від мікропроковзування в місці контакту кулі внаслідок різного радіуса кочення по довжині плями контакту.

Основний матеріал досліджень .Розглянемо спочатку схему дотику куля-площина. Збільшення контактуючих тіл знаходиться із теорії контактних деформацій Герца [4].

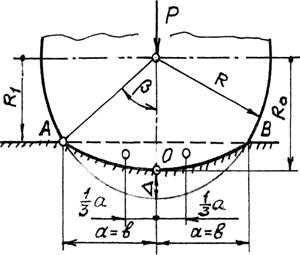
Рис. 1

Будемо вважати, що максимальна деформація кулі в точці (рис. 1) складає половину від . Це припущення може бути перевірене так. Довжина хорди АВ складає 2а і висота сегменту складає , а сума повинна складати радіус кулі. В подальшому буде доведено, що отримана величина радіуса буде відрізнятись від дійсного менше, чим на 1%. Отже, зближення тіл при контакті відбувається за рахунок місцевих деформацій.

Виходячи з цього

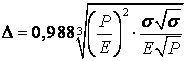. (1)

Радіус кулі визначимо виходячи із теорії контактних напружень Герца

. (2)

Радіус кулі в точці складе

. (3)

Оскільки півширина плями контакту

, (4)

то його радіус в точці із рис. 1

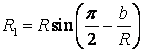. (5)

Якщо припустити, що радіус кулі змінюється від точки до точки по трикутнику, то середня швидкість проковзування

, (6)

де кутові швидкості

, (7)

При навантаженні на кулю і коефіцієнті тертя ковзання потужність на ковзання

. (8)

Потужність; необхідна на подолання загального опору руху кулі яка включає чисте кочення і проковзування

, (9)

де – коефіцієнт тертя кочення.

Нами [5] доведено, що величинапри початковому точковому контакті знаходиться із виразу

. (10)

Прирівнявши вирази (8) і (9) можна знайти приведений коефіцієнт тертя кочення від проковзування

, (11)

Формула (10) отримана експериментально – аналітично. Оскільки експерименти проводились для кранових коліс при (сталь по сталі без змащення), то для визначення коефіцієнта тертя кочення від чистого кочення необхідно із загальної величини (10) відняти величину, яка припадає на ковзання (11) при і ця величина буде постійною при любім

. (12)

Залежності від коефіцієнта тертя ковзання (змащення рідинне у масляній ванні; ‑ змащення густе; відсутність змащення) приведеного коефіцієнта тертя кочення від проковзування та процентні складові від коефіцієнта тертя кочення при показані на рис. 2а.

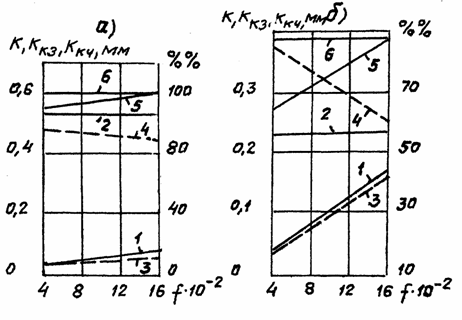
Рис. 2. Залежності від коефіцієнта тертя ковзання кулі по площині (а): 1 - приведеного коефіцієнта тертя кочення від ковзання; 2 - значення коефіцієнта тертя чистого кочення; 3 - процентна складова в ; 4 - процентна складова чистого кочення в ; 5 - сумарна величина коефіцієнта тертя кочення з врахуванням проковзування; 6 - коефіцієнт тертя кочення при ; (б) - те ж для схеми контакту сферичне тіло-жолоб.

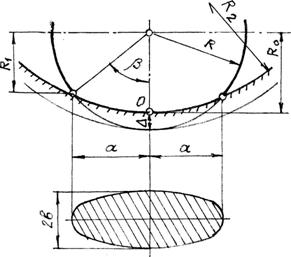
Розглянемо цю ж задачу для схеми дотику сферичне тіло – круговий жолоб (рис. 3).

Рис. 3. Розрахункова схема для дотику сферичне тіло – круговий жолоб

Місцева деформація кулі при умові що радіус жолоба

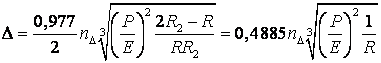, (13)

де - коефіцієнт, який залежить від тих параметрів, що і .

Радіус кулі знайдеться із виразу

. (14)

Половина довжини плями контакту

. (15)

Півширина плями контакту знайдеться із виразу (15) при заміні на .

В подальших розрахунках необхідно скористуватись формулами (5) – (15).

Залежності від коефіцієнта тертя ковзання при схемі контакту сферичне тіло – круговий жолоб величин, що і на рис. 2 показані на рис. 2 б).

Аналіз отриманих формул і графіків на рис. 2 дозволяє зробити такі висновки і пропозиції:

- приведений коефіцієнт тертя кочення від проковзування залежить від схеми контакту кулі та виду змащення і складає при, наприклад, ‑ 42% при схемі дотику сферичне тіло – жолоб і 14% при схемі дотику куля – площина;

- загальна величина коефіцієнта тертя кочення (приведений від ковзання плюс чисте кочення) зменшується зі зменшенням коефіцієнта тертя ковзання і складає при .

Біля 92 % від величини при при схемі дотику куля – жолоб;

- зменшення опору коченню при змащенні зменшує момент на пересування, тому, для усунення проковзування при прискоренні, необхідно зменшувати його величину.

Література

1. Джонсон К. «Механика контактного взаимодействия». – М.: Мир, 1989.-510 с.

2. Тabor D. The mechanism of rolling friction: the elastic range. - Proc. Roy. Sos., 1955 – P. 198.

3. Reynolgs O. On rolling friction. – Philos. Trans. Roy. Soc.,1875. - P.155

4. Справочник по сопротивлению материалов/ Писаренко Г. С., Яковлев А. П., Матвеев В.В. –К.: Наук. Думка, 1988.-736с.

5. Бондаренко Л. М. Аналітичні залежності для визначення коефіцієнта тертя кочення для найбільш вживаних схем дотику // Техніка будівництва, № 11, 2002. – 32-35.