УДК 625.73

Главацкий К.Ц., Богомаз В.Н., Проскурня В.Н., Черкудинов В.Э.

Днепропетровский национальный университет

железнодорожного транспорта им. акад. В. Лазаряна

ВЛИЯНИЕ ПАРАМЕТРОВ ГРУНТОУПЛОТНЯЮЩЕГО КАТКА НА УГОЛ ПОВОРОТА ДЕБАЛАНСА НА ПЕРЕХОДНЫХ РЕЖИМАХ ЕГО РАБОТЫ

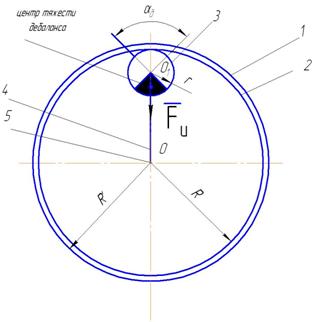
Рассмотрим элементарную часть контура, состоящего из установленного внутри вальца 1 малого зубчатого колеса со смещенным центром тяжести 3, закрепленного на водиле 4, вращающемся вокруг продольной оси вальца 5. Это колесо находится в зацеплении с зубчатым венцом 2, жестко закрепленным на внутренней поверхности вальца 1, (рис. 1). Ранее были рассмотрены случаи, когда каток двигался равномерно, причем в начале отсчета времени малое зубчатое колесо имело постоянную скорость и находилось в крайнем верхнем положении так, что смещенный центр тяжести дебаланса находился на вертикальной оси снизу от центра колеса – точки O₁.

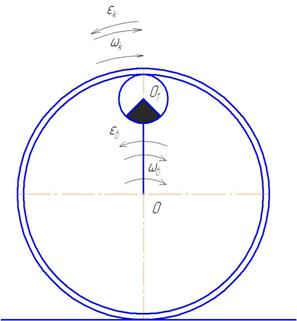
В этой работе учтены начальные положения водила и центра тяжести дебаланса , отсчитываемые от вертикали по часовой стрелке. Движение катка и водила равноускоренное или равнозамедленное с угловыми ускорениями соответственно и , (рис. 2).

1. Каток движется с угловой скоростью ; водило неподвижно (), тогда угол поворота центра эксцентрика относительно вертикальной оси:

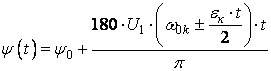, (1)

где - передаточное число в зубчатом зацеплении при вращении вальца; - момент времени, с; знак в формуле (1) означает, что движение может быть, как равноускоренное, так и равнозамедленное.

Рис. 1. Схема катка (1 – внешняя поверхность вальца; 2 – внутренняя поверхность вальца с зубчатым венцом; 3 – дебаланс с зубчатым зацеплением; 4 – водило; 5 – продольная ось вальца)	Рис. 2. Схема направлений движения катка

При этом угол поворота водила – неизменный, . Если , то необходимо от результата отнять целое число периодов вращения колеса.

2. Вариант, когда ; угол поворота центра тяжести дебаланса относительно вертикальной оси находится из зависимости 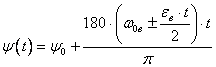(2):

. (2)

Алгоритм получения результата в последующих случаях тот же, что и в предыдущем пункте. При этом угол поворота водила во всех случаях, когда водило движется, находится из зависимости

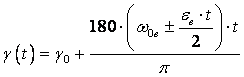. (3)

3. Случай, когда , тогда угол поворота центра тяжести дебаланса относительно вертикальной оси находится из зависимости (3):

, (4)

где - передаточное число в зубчатом зацеплении при вращении водила.

В этом случае результат вычисления угла может оказаться отрицательным. Тогда это означает, что дебаланс повернулся в направлении против движения катка относительно вертикальной прямой, проходящей через центр малого зубчатого колеса (т.е. против часовой стрелки).

4. Случай, когда , тогда угол поворота центра тяжести дебаланса относительно вертикальной оси находится из зависимости (4):

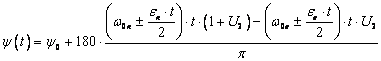. (5)

Если же водило вращать в сторону, противоположную направлению движения катка, то угол поворота центра тяжести дебаланса относительно вертикальной оси по формуле 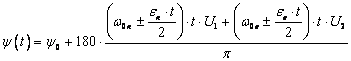(6):

. (6)

Все рассмотренные случаи относятся к относительно стабильным, т.е. характер движения малого зубчатого колеса не меняется, что позволяло нам в каждом конкретном случае использовать только одну из пяти вышеприведенных формул, ограничивая при этом диапазон изменения соответствующих угловых скоростей и ускорений. Но не исключены случаи, что при работе этого контура необходимо будет менять характер движения малого зубчатого колеса. Алгоритм расчета угла при изменении характера движения малого зубчатого колеса приведен ниже.

Допустим, что и , тогда в определенный момент времени получится, что . В этом случае использовать одну из пяти приведенных зависимостей для определения окончательного угла нельзя.

Время, втечение которого будет иметь место , найдем по формуле:

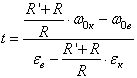. (7)

Тогда зависимость для определения угла поворота центра тяжести дебаланса относительно его вертикальной оси при изменении характера движения малого зубчатого колеса приведен ниже будет иметь следующий вид:

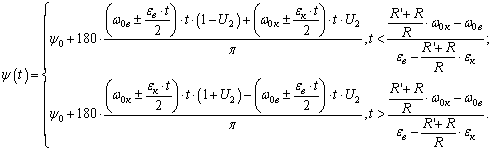(8)

Выводы:

1. Предложен вариант интенсификации работы катка с гладким вальцом, заключающийся в использовании силы инерции, вращающегося по внутренней поверхности вальца малого зубчатого колеса со смещенным центром тяжести.

2. Предложена методика определения угла поворота центра тяжести дебаланса относительно вертикальной оси в любой момент времени в зависимости от угловых скоростей водила и вальца и ускорений в целом, а также передаточных отношений U₁ и U₂, что позволяет определить направление силы инерции от дебаланса.

3. Представлены графические зависимости в виде поверхностей, показывающие значения угла поворота центра тяжести дебаланса относительно вертикальной оси для разных случаев соотношений между параметрами, описанными в пунктах 1-4.

4. Предложен вариант расчета угла поворота центра тяжести дебаланса относительно вертикальной оси при изменяющихся режимах вращения малого зубчатого колеса и вальца в целом.