Мельник В.Н., Карачун В.В., Кладун Е.А.
Национальный
технический университет Украины «КПИ»
ОСОБЕННОСТИ
ПОСТРОЕНИЯ РАСЧЕТНЫХ МОДЕЛЕЙ ПРИБОРОВ ИНЕРЦИАЛЬНОЙ НАВИГАЦИИ
Нашедшие
широкое применение в авиационной и ракетно-космической технике поплавковые
гироскопы, как оказалось, в натурных условиях имеют дополнительные погрешности
при действии проникающего акустического излучения [1, 2, 3]. Картина
усложняется еще тем, что окружающая поплавок с гироагрегатом тяжелая жидкость
является хорошим проводником звука и, таким образом, излучение проходит внутрь
прибора не только через опоры, но и через окружающее пространство. Сказанное
предопределяет и структуру построения расчетной модели подвеса гироскопа как
системы с распределенными параметрами, а в зависимости от соотношения между
длиной волны внешнего возмущения и габаритным размером – как равномерно
распределенная нагрузка, либо как волновое воздействие.
Пусть на поплавок, наклонно к его продольной оси, падает
плоская звуковая волна проникающего излучения (рис. 1)
![]() (1)
(1)
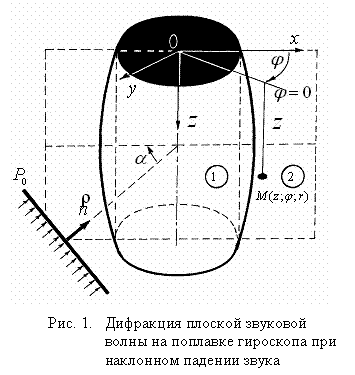
Вектор ![]() , определяющий направление падающей волны, лежит в плоскости
, определяющий направление падающей волны, лежит в плоскости ![]() . Амплитуда принята равной единице.
. Амплитуда принята равной единице.
Задача дифракции формулируется следующим образом. На
поплавок гироскопа падает волна ![]() . В результате рассеяния возникает новое поле
. В результате рассеяния возникает новое поле ![]() , которое можно представить в виде
, которое можно представить в виде
![]() , (2)
, (2)
где ![]() - рассеянное
поверхностью
- рассеянное
поверхностью ![]() поплавка звуковое
поле. Требуется определить
поплавка звуковое
поле. Требуется определить ![]() таким образом, чтобы
полное поле
таким образом, чтобы
полное поле ![]() на поверхности
поплавка удовлетворяло одному из следующих граничных условий:
на поверхности
поплавка удовлетворяло одному из следующих граничных условий:
![]() , дифракция звука на абсолютно мягкой поверхности (задача
Дирихле);
, дифракция звука на абсолютно мягкой поверхности (задача
Дирихле);
![]() , дифракция звука на абсолютно жесткой поверхности (задача
Неймана);
, дифракция звука на абсолютно жесткой поверхности (задача
Неймана);
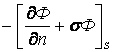 , дифракция звука на импедансной поверхности (смешанная
краевая задача). Здесь
, дифракция звука на импедансной поверхности (смешанная
краевая задача). Здесь ![]() для гармонического
колебательного движения.
для гармонического
колебательного движения.
Величина импеданса ![]() поверхности
поверхности ![]() определяется отношением
звукового давления к нормальной составляющей колебательной скорости (со знаком “минус”),
то есть
определяется отношением
звукового давления к нормальной составляющей колебательной скорости (со знаком “минус”),
то есть
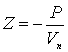 .
(3)
.
(3)
Выбор знака обусловлен следующим
обстоятельством. У выпуклой поверхности ![]() нормаль направлена
наружу и положительное значение колебательной скорости
нормаль направлена
наружу и положительное значение колебательной скорости ![]() также направлено во
внешнюю область “
также направлено во
внешнюю область “![]() , она будет стремиться прогибаться во внутреннюю область “
, она будет стремиться прогибаться во внутреннюю область “
Для
вогнутой поверхности поплавка, нормаль направлена во внутреннюю область “
![]() ,
,
где ![]() - коэффициент;
- коэффициент; ![]() - плотность среды.
- плотность среды.
Четвертая
краевая задача
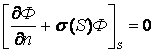
называется смешанной. Из нее, как частные случаи, ![]() ,
, ![]() ,
, ![]() , следует, соответственно, первая, вторая и третья задачи.
, следует, соответственно, первая, вторая и третья задачи.
Существует еще обширный класс проблем,
для которых граничные условия являются более сложными и зависят не только от
первой производной потенциала, но и от производных более высоких порядков. В
общем случае такие граничные условия можно записать в виде
![]() ,
,
где ![]() - дифференциальный
оператор, определяющий свойства поверхности. Если
- дифференциальный
оператор, определяющий свойства поверхности. Если ![]() ,
, ![]() ,
, ![]() , то получаются записанные выше граничные условия.
, то получаются записанные выше граничные условия.
Реальные поверхности являются упругими,
поэтому указанные выше граничные условия должны рассматриваться, как
соотношения, приближенно характеризующие свойства поверхности поплавка.
Звуковое поле вне поплавка ![]() , зона “
, зона “![]() , рассеянной цилиндром
, рассеянной цилиндром ![]() и излучаемого упруго
колеблющейся поверхности
и излучаемого упруго
колеблющейся поверхности ![]() , т.е.
, т.е.
![]() , (4)
, (4)
где
![]() ;
;
 ;
;
![]() ;
;
![]() - волновое число;
- волновое число; ![]() - коэффициенты;
- коэффициенты; ![]() - цилиндрические
функции; 1 – амплитуда падающей
волны.
- цилиндрические
функции; 1 – амплитуда падающей
волны.
Поле внутри поплавка, то есть в зоне “
![]() , (5)
, (5)
где ![]() - коэффициент;
- коэффициент; ![]() - волновое число (5)
внутренней полости.
- волновое число (5)
внутренней полости.
Окончательный вид звуковых полей в
зонах “![]() ,
, ![]() :
:
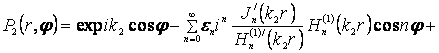
 ; (6)
; (6)
 , (7)
, (7)
где ![]() - механический
импеданс:
- механический
импеданс:
 ;
;
![]()

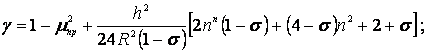
 .
.
Таким образом, построенная расчетная
модель решает не только задачи динамики подвеса гироскопа, но и вопросы
звукоизоляции.
Литература:
1.
Погрешности гироскопического интегратора линейных
ускорений в натурных условиях / Карачун В.В., Мельник В.Н., Лозовик В.Г.,
Одинцов А.А. /Под ред. В.В. Карачуна. – К.: «Корнейчук», 2001. – 144 с.
2.
Карачун В.В., Лозовик В.Г., Мельник В.Н. Дифракция
звуковых волн на подвесе гироскопа. – К.: «Корнейчук», 2000. – 176 с.
3.
Koshljakov V.N., Karachun V.V., Mel’nik
V.N., Saverchenko V.G., Balanin V.Kh. THE SOME ASPECTS OF FLAIGT SAFETY IN
CONDITIONS PENETRATE ACOUSTIC RADIATSON. The World Congress «Aviation sn the
XXI-st Century»,