Технически науки , №2

Рубашка В. П.

Украинская иженерно-педагогической академия, г. Харьков

Математическое моделирование движения частицы в жидкой или газообразной среде

Проблема изучения разделения неоднородных систем непосредственно связана с анализом движения твердой частицы в жидкой или газообразной среде. В исследованиях, посвященных данной проблеме, принято разделять две задачи: задачу свободного осаждения частицы и задачу стесненного осаждения под действием силы тяжести или центробежных сил. В настоящее время использование компьютерной техники в сочетании с современные математическими методами, реализованными в специализированных пакетах программ позволяют построить математическую модель осаждения, которая бы описывала движение частицы как при любых режимах осаждения, так и в периоды ее разгона и при установившемся движении.

За основу построения модели свободного осаждения возьмем уравнение, отражающее общий баланс действующих на частицу сил:

, где - внешняя возмущающая сила (сила тяжести или центробежная сила); - подъемная (архимедова) сила; - сила сопротивления среды. Выражение для возмущающей силы может быть представлено в следующем виде . Здесь m – масса осаждающейся частицы, а – ускорение осаждения. Для осаждения под действием силы тяжести . Архимедова сила принимается пропорциональной массе среды, вытесненной частицей: 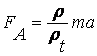, где - плотность среды, - плотность материала частицы.

Сила сопротивления, действующая на частицу поперечного сечения S со стороны среды в соответствии с законом Стокса принимается равной . В последнем выражении коэффициент сопротивления среды поставлен в зависимость от режима осаждения

(1)

где 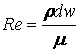- число Рейнольдса, зависящее от скорости осаждения w, диаметра частицы d и вязкости среды осаждения .

В случае осаждения под действием силы тяжести уравнение свободного осаждения примет вид 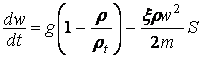. Для сферической частицы

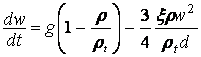(2)

Данное уравнение представляет собой нелинейное дифференциальное уравнение не допускающее аналитического решения. Только в случае ламинарного режима осаждения для уравнение преобразуется к линейному дифференциальному уравнению.

Модель осаждения представленная соотношениями (1) – (2) справедлива для любых режимов свободного осаждения. Ее использование в исследовании разделения сред позволяет провести анализ движения частицы как в периоды разгона, так и в периоды движения с установившейся скоростью.

Моделирование стесненного осаждения существенно усложняется за счет учета дополнительных сил сопротивления, проявляющихся в результате взаимодействия осаждающихся частиц. Детальный учет многообразия силового взаимодействий движущихся частиц выполнить практически невозможно. Поэтому применяют некоторые интегральные оценки, сводящиеся к введению дополнительных коэффициентов в выражении для силы сопротивления, учитывающих дополнительные сопротивления движению частицы. Так предлагается общую силу сопротивления , действующую на осаждающуюся частицу поставить в зависимость от объемной концентрации частиц с помощью некоторой поправочной функции : (3)

где - сила сопротивления при свободном осаждении частицы, а определяется выражением. (4)

Особенностью приведенного выражения поправочной функции является то, что для моделирования свободного осаждения достаточно принять . Тогда и общая сила сопротивления, действующая на осаждающуюся частицу примет вид силы сопротивления при свободном осаждении.

Учитывая (3) уравнение стесненного осаждения сферической частицы примет вид (5)

Приведенное уравнение составлено относительно скорости осаждения . В свою очередь функция поставлена в зависимость от объемной концентрации которая изменяется по глубине осадительной камеры от некоторого своего начального значения до конечного . Таким образом, объемная концентрация является функцией пройденного частицей пути.

Пусть осаждающаяся частица движется вдоль оси . Тогда примем некоторый закон изменения объемной концентрации . Уравнение стесненного осаждения (5) приведем к новой переменной - линейному перемещению осаждающейся частицы вдоль оси . Учитывая связь перемещения и скорости осаждения , получим (6)

Необходимость учета дополнительных сопротивлений, возникающих при стесненном осаждении частицы поставленных в зависимость от объемной концентрации, приводит к описанию процесса осаждения дифференциальным уравнением второго порядка относительно новой переменной – пройденного частицей пути. Помимо соотношений (4), (6) в математическую модель осаждения необходимо включить:

- закон изменения коэффициента сопротивления относительно

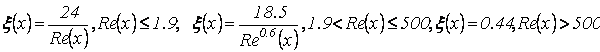(7)

где (8)

- закон изменения объемной концентрации по глубине осадительной камеры

(9)

- начальные условия осаждения при (10)

где начальная координата, а - начальная скорость осаждения.

Модель осаждения представленная соотношениями (4) – (10) позволяет: анализировать стесненное и свободное осаждение частицы; учитывать ламинарный, переходной и турбулентные режимы осаждения; определять не только изменение во времени скорости осаждения, но и рассчитывать перемещения частицы, что является основой для расчета осадительной камеры. В представленной модели учитываются: параметры осаждающейся частицы – ее диаметр и плотность; характеристики среды осаждения – плотность, динамическая вязкость; условия осаждения – характер изменения объемной концентрации твердых частиц по глубине осадительной камеры, начальные положение и скорость осаждения частицы.

В качестве примера рассмотрим задачу стесненного осаждения частицы асбеста в воде при температуре 20⁰ С. При расчетах был прият линейный закон изменения объемной концентрации по глубине осадительной камеры. На рис. 1. приведены результаты расчета скоростей осаждения w частиц различных диаметров.

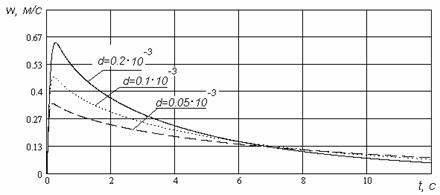
Из расчетов следует, что максимальных скоростей осаждения частицы достигают на первой секунде осаждения. В дальнейшем скорости плавно уменьшаются. Это связано с увеличение сил сопротивления обусловленных увеличением объемной концентрации осаждающихся частиц. Начиная с 7-й секунды скорости частиц различного веса практически выравниваются и начинается режим так называемого «солидарного осаждения». Такой эффект проявляется у дна осадительной камеры и характеризуется уплотнением зоны осадка.

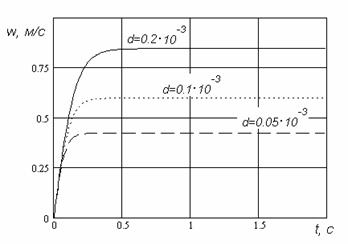
На рис. 2. представлены результаты расчета для тех же частиц, но в случае их свободного осаждения. Для моделирования такого режима достаточно в законе осаждения положить равным 0 начальное и конечное значения объемной концентрации. При принятых значениях поправочная функция и уравнение (6) автоматически преобразуется в уравнение свободного осаждения.

Из приведенных на рис. 2. графиков отчетливо видно два периода в движении осаждающихся частиц. Первый – это кратковременный период разгона при котором частица достигает установившейся скорости, а сила сопротивления со стороны среды достигает значения веса частицы. Второй период – период равномерного осаждения с установившейся (Стоксовой) скоростью.

В заключении следует отметить, что построенную модель осаждения следует отнести к классу обобщенных математических моделей, поскольку единый набор математических зависимостей позволяет моделировать различные процессы осаждения. Причем описание того ил иного процесса проводится на уровне исходных данных, характеризующих этот процесс без преобразования модели в целом.