Посмитюха А.П., Ямковенко О.Н., Бондаренко Л.Н.

Днепропетровский национальный университет железнодорожного транспорта им. В. Лазаряна (ДІІТ)

СВЯЗЬ МЕЖДУ НАТЯЖЕНИЕМ И УСТОЙЧИВОСТЬЮ ТЯГОВЫХ ОРГАНОВ КОВШОВЫХ ЭЛЕВАТОРОВ

Пусть закон изменения силы, возбуждающей рабочую и холостую ветви вертикального ковшового элеватора описывается уравнением

, (1)

где - максимальное усилие при зачерпывании;

- закон изменения усилия за период зачерпывания.

Дифференциальное уравнение поперечных колебаний тягового органа в этом случае записывается в виде

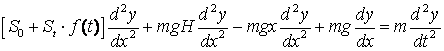. (2)

Решение этого уравнения будем искать в виде

. (3)

Подставим значения из (3) в (2), умножим на и проинтегрируем от 0 до . После ряда преобразований, получим

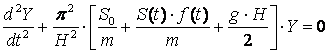. (4)

Решение этого уравнения зависит от вида функции .

Пусть

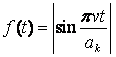, (5)

где ‑ шаг ковшей.

Разложим функцию (5) в ряд Фурье и введем безразмерные переменные и , где представляет некоторое характерное значение , а . Тогда уравнение (4) преобразуется к виду

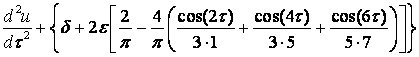, (6)

где ; .

В реальных элеваторах малая величина, поэтому для решения уравнения (6) можно применить метод растянутых параметров, суть которого заключается в том, что решение и параметр разлагаются в ряд по степеням малого параметра ( для м)

;

. (7)

Отметим, что решение уравнения (6) можно получить любым численным методом. О пригодности выбранных параметров элеватора при этом судят по ограниченным или неограниченным решениям. Рассматриваемая методика позволит для заданного (известного) закона изменения усилия зачерпывания получить переходные кривые, определяющие области устойчивости и неустойчивости колебаний. Имея уравнение переходной кривой, можно варьировать параметрами конвейера, не решая каждый раз уравнение (6).

Запишем решение уравнения (6), а также уравнение переходной кривой (7) во втором приближении для случая [1]

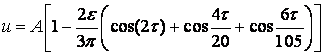, . (8)

Одна из переходных кривых, отделяющая области устойчивости и неустойчивости, выходит из точек , и описывается вторым уравнением (8). Первое уравнение (8) показывает, что на этой кривой решение имеет периодичность .

При получим уравнения, два из которых описывают переходные кривые

;

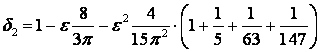, (9)

а два других

;

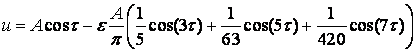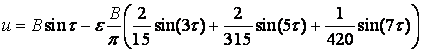, (10)

показывают, что в общих случаях решения имеют периодичность ().

При значениях от 0 до 0,8 (для реальных элеваторов) получим области устойчивости параметров для случая изменения усилия зачерпывания по принятому выше закону.

Если усилие зачерпывания изменяется по закону, отличному от принятого, то формулы (9), (10) будут отличаться в указанных диапазонах только величинами второго и третьего порядков малости, поэтому для практических расчетов этими формулами можно пользоваться при любом реальном законе изменения усилия зачерпывания.

Рассмотрим устойчивые и неустойчивые колебания рабочей ветви элеватора ЭЛГ-350. Значение можно определить экспериментально или при известном законе изменения усилия зачерпывания за период. Если мощность, затрачиваемая на зачерпывание материала

, (11)

то из условия равенства работ за период найдем

. (12)

Определив из формулы (6) и , найдем изображающие точки на диаграмме (рис.1). Расположение точек для элеватора ЭЛГ-350 находятся на линии 5 и колебания рабочей ветви устойчивы.

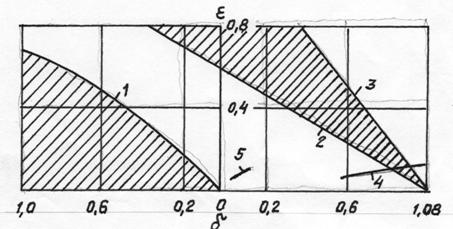
Рис. 1 - Области устойчивости и неустойчивости (заштрихованы) ветвей ковшовых элеваторов:

1 ‑ переходная кривая (формула (9) первое уравнение); 2 ‑ переходная кривая (формула (9) второе уравнение); 3 ‑ переходная кривая (формула (10) первое уравнение); 4 ‑ линия изображающих точек при , м/с; 5 - то же при , м/с.

Если напряжение увеличить, например в 5 раз, а скорость уменьшить до 0,5 м/с, то изображающие точки будут находиться на линии 4 и колебания тягового органа на участке пересечения линий 2 и 3 будут неустойчивы, что соответствует м. Следовательно, элеватор такой высоты применять нельзя, поскольку амплитуды его поперечных колебаний будут значительными.

Литература

1. Найфе А. Введение в метод возмущений. – М.: Мир, 1984. -536 с.