Математика/1.Диференціальні і інтегральні рівняння

К. фіз.–мат. н. Малицька Г.П.

Прикарпатський національний університет ім. В. Стефаника

Поведінка розв’язків задачі Коші при для деяких класів рівнянь типу Колмогорова

Позначення: , натуральні числа .,,,,, , , , .

Розглянемо задачу Коші

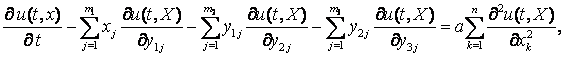(1)

, (2)

де - вимірна, обмежена функція в ,.

Фундаментальний розв’язок (1)–(2) має вигляд [1]:

,

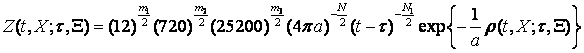де

– сімейство поверхонь рівня фундаментального розв’язку задачі (1), (2). Через позначимо тіло, обмежене еліпсоїдом

, (3)

де – змінна точка, – об’єм тіла обмеженого поверхнею:

Нехай середнє значення по тілу , обмеженому поверхнею (3).

Означення 1 Функція має граничне середнє по тілах при , якщо існує .

Точкова стабілізація інтеграла Пуассона для задачі Коші (1), (2).

По аналогії до параболічних рівнянь, розв’язок задачі Коші (1), (2)

(4)

назвемо інтегралом Пуассона задачі Коші (1), (2).

Теорема 1. Якщо має граничне середнє по еліпсоїдах , то інтеграл Пуассона (4) стабілізується (прямує при ) до числа

.

Доведення. Розглянемо інтеграл Пуассона для рівняння (1) і введемо заміну змінних інтегрування

, , ,

.

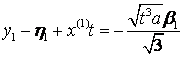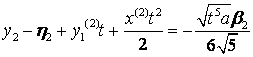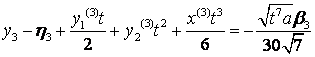Тоді (4) матиме вигляд

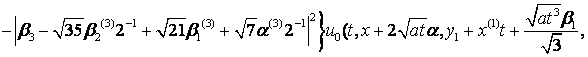
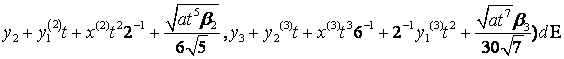, (5)

, , .

Розглянемо додатно визначену квадратичну форму

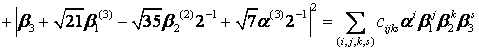, (6)

де ..

В інтегралі (5) перейдемо до нових змінних інтегрування:

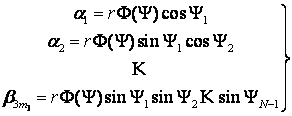, (7)

де , , , , .

Функція визначається рівністю: ,

з , .

Якобіан перетворення (7) , .

Позначимо через

.

Тоді ,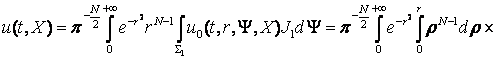

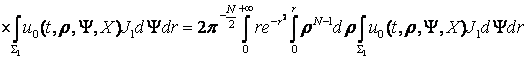де – одинична сфера в . Виділимо :

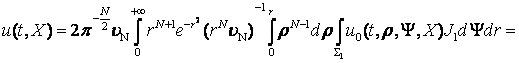
. (8)

Залишається здійснити граничний перехід під знаком інтеграла (8) при . Це можна зробити на основі теореми Лебега, оскільки існує граничне середнє, а із обмеженості безпосередньо випливає рівномірна (по ) обмеженість . Зауважимо, що досить вимагати існування граничного середнього в деякій фіксованій точці , із цього уже безпосередньо випливає існування граничного середнього в будь-якій точці і факт стабілізації на кожному компакті.

Теорема 2. Якщо , то для стабілізації інтеграла Пуассона (4) до нуля необхідно й досить, щоб мала граничне середнє , майже скрізь, рівне нулю.

Доведення. Достатність випливає із теореми 1. Покажемо, що із стабілізації (4) до 0 випливає існування нульового граничного середнього по .

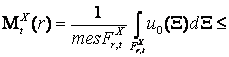
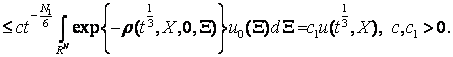(9)

В нерівності (9) замінено об’ємом куба з стороною , який міститься в . Оскільки при із (9) випливає, що при для будь-якого . Теорема доведена.

При , одержимо теореми із [2].

Рівномірна стабілізація інтеграла Пуассона.

Розглянемо задачу Коші для рівняння порядку по змінних :

, (10)

де - параболічний за І. Г. Петровським оператор, . Фундаментальний розв’язок задачі Коші (10), (2) задовольняє нерівності :

,

де , ,

, .

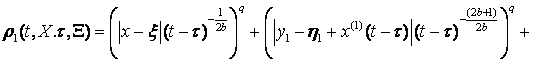
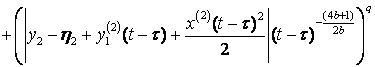
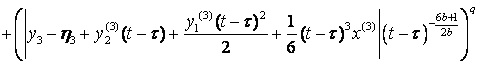Нехай має граничне середнє

,

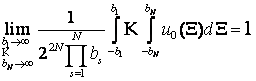де , незалежно одне від одного.

Теорема 3. Для того, щоб інтеграл Пуассона рівняння (10) рівномірно стабілізувався до при необхідно і досить, щоб мала граничне середнє рівне .

Література

1. Малицька Г. П. Побудова фундаментального розв’язку задачі Коші для рівняння дифузії із змінною інерцією // Мат. методи і фіз.–мех. поля. – 1999. – Т. 42, №3. – С. 56–60.

2. Малицкая А. П., Репников В. Д., Эйдельман С. Д. О стабилизации решений задачи Коши для уравнения диффузии с инерцией // Труды НИИМ ВГУ. – Выпуск V. – Воронеж, 1972. – С. 86-92.