УДК 539.4
Прикладная математика и механика
В.С. Ромасько
Харьковский
государственный технический университет строительства и архитектуры. 61002.
Харьков.
Особенности применения принципа подобия кривых
ползучести в теории неравновесных деформационных
процессов
1. Введение
Построение универсальной относительно различных режимов нагружения связи
между макропараметрами модели сплошной среды (напряжений, деформаций, скоростей
деформации и температуры) основано на гипотезе о существовании уравнения
состояния при равной нулю скорости деформации, или кинетического уравнения в
противном случае. Его, обычно, не удается реализовать, так как сплошную среду принято
рассматривать как одноуровневую систему, тогда как реальные материалы являются
многоуровневыми иерархическими системами. На одних иерархических уровнях равновесное
состояние достигается быстро, о чем свидетельствует обращение в ноль скорости
деформации, а на других уровнях процесс деформации на протяжении длительного
времени продолжается с конечной скоростью деформации [1], [2]. Определяющие уравнения, отображающие сигналы на входе (область
определения) на сигналы на выходе (область значений), могут быть представлены в
виде функции, функционала, или оператора. При постоянной температуре для равной
нулю скорости деформации связь между напряжениями и деформациями при одноосном
напряженном состоянии может быть описана функцией. Для измерения равновесной
деформационной кривой требуется затратить много средств и времени, поэтому она
измеряется не в прямых опытах, а косвенными методами. В случае постоянной
температуры, но отличной от нуля скорости деформации связь между напряжениями и
деформациями, имеющая вид функционала, также не может быть построена, так как
задача построения функционала по результатам испытаний конечного числа образцов
материала не поставлена математически.
В связи с невозможностью построения
функционала, описывающего соотношение между напряжениями и деформациями в общем
случае, полезными оказались принципы подобия изотермических деформационных кривых
напряжения – деформации в серии кривых, полученных при различных скоростях
нагружения, и принцип подобия кривых ползучести, измеренных при различных
напряжениях. В известной монографии Ю.Н. Работнова [3] (на стр.196) в связи с
гипотезой уравнения состояния упоминаются публикации Людвика, относящиеся к
началу прошлого века, книга Надаи, написанная в тридцатые годы, и статья
Давенпорта, где введены представления о двух теориях упрочнения (time hardening theory - первая) и (strain hardening theory - вторая). Наблюдаемое в условиях
изотермической ползучести подобие первичных и изохронных кривых ползучести
использовано Ю.Н. Работновым для проверки первой и второй теорий упрочнения. К
сожалению, при проведении сравнения этих теорий упрочнения с данными опытов
Ю.Н. Работновым были допущены сразу две ошибки: была принята не верная первая
теория старения и отвергнута более правильная вторая теория упрочнения. Этими
ошибками Ю.Н. Работнов не ограничился и продолжал их плодить в таком
количествее, что создается впечатление, будто они делаются им сознательно, с
целью запутать читателя. Версия о том, что Ю.Н. Работнов не понимал сути
вопросов, о которых писал, маловероятна. Тем не менее, им была дана не верная
рекомендация: «Чтобы получить (по первой теории) кривую ползучести,
соответствующую ступенчатому изменению нагрузки, нужно сдвинуть верхнюю кривую
(соответствующую новому возросшему уровню напряжения) вправо (по оси времени)
до совпадения с точкой (моментом времени, когда произошел скачек напряжения)».
Правильная вторая теория упрочнения была отброшена: Вторую теорию Ю.Н. Работнов
назвал, теорией старения, тогда как следовало бы говорить не о старении, а об
упрочнении. Кроме того, нужно было бы переносить верхнюю кривую параллельно
себе вниз до совпадения по деформациям. Далее Ю.Н. Работнов, ссылаясь на
приближенный характер теории, отмечал: «Разница в предсказаниях двух теорий
оказывается чрезвычайно резкой, притом с опытом гораздо лучше согласуется
теория упрочнения». В подтверждение своих теоретических положений Ю.Н. Работнов
приводил данные опытов Наместникова и Хвостункова для сплава Д-16Т: «Сравнение
с экспериментом показало, что теория упрочнения дает удовлетворительные
результаты, а теория старения сильно преуменьшает скорость ползучести после
изменения нагрузки. В то же время предсказания теории упрочнения не являются
вполне точными, обнаруживаются систематические отклонения, которые особенно
проявляются при наличии нескольких ступеней изменения напряжения». Несмотря на
то, что Ю.Н. Работнов подчеркивал приближенность методов расчета конструкции в
условиях изотермической ползучести, требуется дать ясное изложение принципа
подобия кривых ползучести в рамках одноуровневых моделей материала.
Для описания кривых ползучести в
рамках традиционной механики деформируемого твердого тела, использующей
гипотезу о существовании для параметров макро уровня уравнения состояния,
связывающего между собой скорость изотермической ползучести ![]() , напряжение
, напряжение ![]() и накопленную
деформацию ползучести
и накопленную
деформацию ползучести ![]()
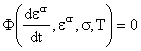 , (1.1)
, (1.1)
Ю.Н. Работновым предложено использовать зависимость
деформации ![]() от времени
от времени ![]() в виде произведения
в виде произведения
![]() (1.2)
(1.2)
функции напряжения ![]() на функцию времени
на функцию времени ![]() . Ту же самую функциональную зависимость можно представить
иначе
. Ту же самую функциональную зависимость можно представить
иначе
![]() , (1.3)
, (1.3)
откладывая по осям координат
напряжения ![]() и деформации
и деформации![]() за вычетом упругих деформаций, совпадающих по фазе с
напряжениями. Здесь
за вычетом упругих деформаций, совпадающих по фазе с
напряжениями. Здесь ![]() ,
, ![]() , также как и
, также как и ![]() ,
, ![]() некоторые, подбираемые
для описания данных опытов и характеризующие свойства материала, функции,
существование которых не очевидно.
некоторые, подбираемые
для описания данных опытов и характеризующие свойства материала, функции,
существование которых не очевидно.
Для наглядности, но не для
обоснования Ю.Н. Работнов использовал понятие о мгновенных деформационных
кривых, записав функцию ![]() с некоторыми постоянными
коэффициентами
с некоторыми постоянными
коэффициентами ![]() и
и ![]()
![]() . (1.4)
. (1.4)
Мгновенной деформационной кривой (![]() ) на рис.1 при
) на рис.1 при ![]() соответствует не
зависящее от времени базовое выражение
соответствует не
зависящее от времени базовое выражение
![]() . (1.5)
. (1.5)
Остальные деформационные кривые 2 и 3
на рис.1, названные Ю.Н. Работновым изохронными, соответствую сечениям ![]() ,
, ![]() серии кривых
ползучести (1.2).
серии кривых
ползучести (1.2).
С известной
долей погрешности в рамках приближенного подхода принцип подобия кривых
ползучести, описываемых выражением (1.2), и деформационных кривых, описываемых
формулой (1.3), нашел экспериментальное подтверждение и даже стал применяться
для сравнения между собой различных технических теорий изотермической
ползучести в форме старения
![]() , (1.6)
, (1.6)
течения
![]() , (1.7)
, (1.7)
и упрочнения
![]() . (1.8)
. (1.8)
при ступенчатом изменении напряжения.
На рис.2 приведены две кривые ползучести при напряжениях ![]() и
и ![]() .
.
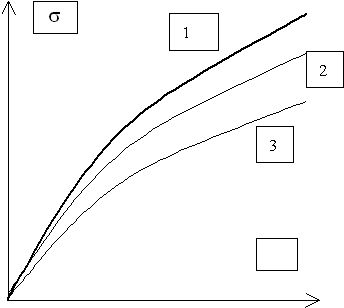
Рис. 1. Изохронные деформационные кривые: 1- мгновенная
деформационная кривая, соответствующая ![]() , 2 -
, 2 - ![]() , 3 -
, 3 - ![]() .
.
До тех пор, пока в
образце поддерживается напряжение ![]() , ползучесть следует нижней кривой. В момент времени
, ползучесть следует нижней кривой. В момент времени ![]() скорость деформации
скорость деформации ![]() увеличивается в
результате внезапного скачка напряжения от величины
увеличивается в
результате внезапного скачка напряжения от величины ![]() до
до ![]() . По теории старения (1.6) изменение напряжения должно
сопровождаться изменением деформации. По теории течения (1.7) и по теории
упрочнения (1.8) изменение напряжения должно сопровождаться изменением скорости
деформации. Данные опытов свидетельствуют о том, что в момент изменения
напряжения скачком меняется не деформация ползучести, а ее скорость. Ю.Н.
Работнов предположил, что, согласно принципу подобия кривых ползучести, скорость
деформации в момент скачка напряжения представляет собой угловой коэффициент
касательной к верхней кривой ползучести в точке, имеющей ту же ординату. По
мнению Ю.Н. Работнова, кривая ползучести после увеличения напряжения будет
повторением кривой ползучести при постоянном напряжении
. По теории старения (1.6) изменение напряжения должно
сопровождаться изменением деформации. По теории течения (1.7) и по теории
упрочнения (1.8) изменение напряжения должно сопровождаться изменением скорости
деформации. Данные опытов свидетельствуют о том, что в момент изменения
напряжения скачком меняется не деформация ползучести, а ее скорость. Ю.Н.
Работнов предположил, что, согласно принципу подобия кривых ползучести, скорость
деформации в момент скачка напряжения представляет собой угловой коэффициент
касательной к верхней кривой ползучести в точке, имеющей ту же ординату. По
мнению Ю.Н. Работнова, кривая ползучести после увеличения напряжения будет
повторением кривой ползучести при постоянном напряжении ![]() .
.
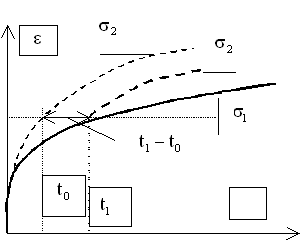
Рис.2. Иллюстрация применения
принципа подобия кривых ползучести по Ю.Н. Работнову. Скачок напряжения от ![]() до
до ![]() сопровождается скачком
скорости деформации до величины, равной угловому коэффициенту касательной к
верхней кривой ползучести в «точке, имеющей ту же ординату».
сопровождается скачком
скорости деформации до величины, равной угловому коэффициенту касательной к
верхней кривой ползучести в «точке, имеющей ту же ординату».
В приведенных
рассуждениях Ю.Н. Работнова учитывается только одно из двух возможных правил
выбора точки на верхней кривой ползучести, где вычисляется скорость. Вместо
слов « в точке, имеющей ту же ординату» можно говорить о « точке, имеющей ту же
абсциссу». Очевидно, что Ю.Н. Работнов выбрал не лучший вариант, говоря о той
же ординате, так как приравнивание скоростей по ординате соответствует первой (time hardening) теории. Более точной второй (strain hardening) теории упрочнения соответствовала
бы фраза: «Скачок напряжения от ![]() до
до ![]() сопровождается скачком
скорости деформации до величины, равной угловому коэффициенту касательной к
верхней кривой ползучести в «точке, имеющей ту же абсциссу».
сопровождается скачком
скорости деформации до величины, равной угловому коэффициенту касательной к
верхней кривой ползучести в «точке, имеющей ту же абсциссу».
С учетом указанных
недостатков в рассуждениях Ю.Н. Работнова в данной работе для описания
зависимости деформации ползучести от времени при постоянном напряжении используются
две группы уравнений: уравнение состояния на мезоуровне, формулируемое в
равновесных напряжениях и деформациях и кинетическое уравнение, устанавливающее
связь между параметрами состояния мезо и макроуровня. Из уравнения состояния и
кинетического уравнения следуют технические теории изотермической ползучести, а
принцип подобия кривых ползучести является следствием уравнения состояния на
мезоуровне, описывающего равновесный процесс деформационного упрочнения. Время
в уравнении ползучести появляется в результате интегрирования кинетического уравнения
при заданном режиме изменения нагрузки, т.е. уравнения теории старения
описывают траекторию процесса деформации в конкретных условиях.
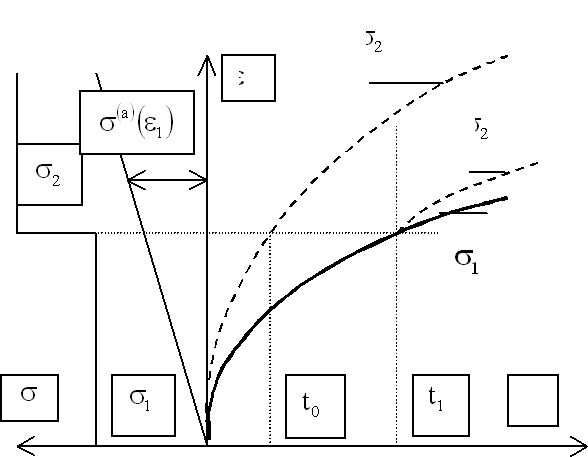
Рис. 3. Иллюстрация применения
принципа подобия кривых изотермической ползучести при ступенчатом изменении
нагрузки. Скачок напряжения от ![]() до
до ![]() при деформации
при деформации ![]() сопровождается скачком
скорости деформации до величины, равной угловому коэффициенту касательной к
верхней кривой ползучести в «точке, имеющей ту же абсциссу – время
сопровождается скачком
скорости деформации до величины, равной угловому коэффициенту касательной к
верхней кривой ползучести в «точке, имеющей ту же абсциссу – время ![]() ». На величину скорости деформации оказывает влияние
эффективное напряжение.
». На величину скорости деформации оказывает влияние
эффективное напряжение.
Процесс сопротивления
деформации материала как иерархической системы рассматривается в фазовом
пространстве равновесных напряжений на мезо и макроуровнях. На рис. 3 график
уравнения состояния представлен линейной зависимостью равновесных напряжений от
деформации ползучести. Гипотеза о полилинейной формы записи уравнения состояния
на мезоуровне предложена новая формулировка принципа подобия кривых ползучести,
позволяющая описать зависимость деформации от времени при ступенчатом изменении
нагрузки.
2. Параметры состояния иерархической системы
Рассматривается
процесс сопротивления сплава титана Ti с 6% алюминия Al и 4 % ванадия V деформации ползучести при
температуре 650 °С. Материал представляет собой
иерархическую систему. На макроуровне состояние определяется напряжениями s и
деформациями e. На мезоуровне дискретные элементы структуры распределены
по равновесным напряжениям ![]() , отнесенным
, отнесенным ![]() к полным
макронапряжениям s, с плотностью
к полным
макронапряжениям s, с плотностью ![]() . Величину макронапряжения можно представить в виде суммы
. Величину макронапряжения можно представить в виде суммы
![]() (2.1)
(2.1)
математического ожидания 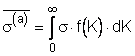 , зависящего при изотермической ползучести от величины деформации, равновесного и,
зависящего, кроме того, от скорости деформации
, зависящего при изотермической ползучести от величины деформации, равновесного и,
зависящего, кроме того, от скорости деформации ![]() ползучести,
эффективного
ползучести,
эффективного ![]() напряжений.
напряжений.
3. Кинетическое уравнение сопротивления деформации ползучести
Связь между параметрами
состояния мезо и макроурвней при изотермической ползучести устанавливает кинетическое
уравнение [2], записанное в безразмерном и универсальном для различных материалов
виде
![]() . (3.1)
. (3.1)
Здесь 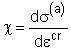 - коэффициент
равновесного деформационного упрочнения,
- коэффициент
равновесного деформационного упрочнения, ![]() -коэффициент вязкости течения с малой скоростью (вязкость
практически неповрежденной структуры по выражению П.А. Ребинедера).
-коэффициент вязкости течения с малой скоростью (вязкость
практически неповрежденной структуры по выражению П.А. Ребинедера).
4. Уравнение состояния на мезоуровне
Уравнение
состояния на мезоуровне, описывающее равновесную деформационную кривую, с
помощью нелинейных
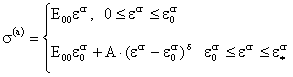 (4.1)
(4.1)
или кусочно-линейных функций
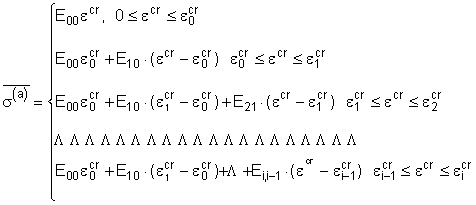 . (4.2)
. (4.2)
Здесь приняты следующие обозначения
![]() (4.3)
(4.3)
средних равновесных напряжений ![]() (i=1,2..) в опорных точках
(i=1,2..) в опорных точках ![]() равновесной
деформационной кривой
равновесной
деформационной кривой ![]() ;
; ![]() ,
,![]() ...
...![]() -тангенциальных равновесных модулей.
-тангенциальных равновесных модулей.
5. Интегрирование кинетического уравнения при ступенчатом изменении
нагрузки в случае полилинейного уравнения состояния
В
случае полилинейной формы записи уравнения состояния (4.2) при заданном
ступенчатом изменении нагрузки
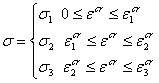 (5.1)
(5.1)
может быть получено решение кинетического
уравнения
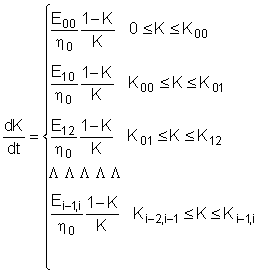 (5.2)
(5.2)
в неявном относительно ![]() виде:
виде:
 (5.3)
(5.3)
6. Представление
решения кинетического уравнения в явном относительно K виде
Пусть на основе
неявного относительно ![]() задания решения
конститутивного уравнения
задания решения
конститутивного уравнения
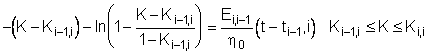 , (6.1)
, (6.1)
требуется построить его приближенное
выражение в явном виде, используя разложение логарифма в ряд и ограничившись
первыми двумя членами
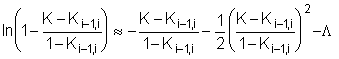 . (6.2)
. (6.2)
Тогда, с учетом разложения (5.2) соотношение (5.1) упрощается
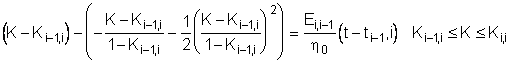 (6.3)
(6.3)
и может быть решено относительно переменной
![]() (6.4)
(6.4)
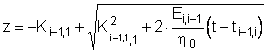 . (6.5)
. (6.5)
С учетом полученного приближенного решения
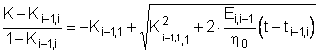 (6.6)
(6.6)
можно записать нулевое ![]()
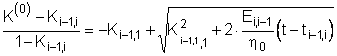 , (6.7)
, (6.7)
первое ![]()
 ,, (6.8)
,, (6.8)
и второе ![]()
 (6.9)
(6.9)
приближения, подставив в формулу требуемое выражение К
 . . (6.10)
. . (6.10)
Можно также воспользоваться приближенными явными зависимости
К(t) в нулевом,
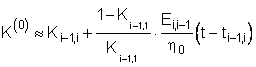 (6.11)
(6.11)
и в первом приближениях
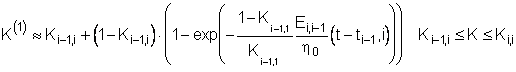 (6.12)
(6.12)
Смысл нулевого приближения очевиден
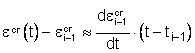 . (6.13)
. (6.13)
Для первого приближения допустима следующая интерпретация:
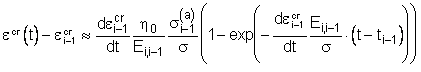 . (6.14)
. (6.14)
При ступенчатом изменении нагрузки
приращение деформации ползучести на каждом отрезке времени, где уровень
напряжения фиксирован, определяется произведением скорости деформации
ползучести в момент времени ![]() на функцию влияния
на функцию влияния
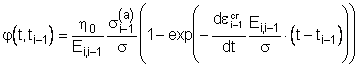 , (6.15)
, (6.15)
Функция влияния скорости на
последующую деформацию зависит от величин скорости деформации ![]() и отношения
и отношения ![]() равновесного
напряжения
равновесного
напряжения ![]() к полному
к полному ![]() в начальный момент
времени
в начальный момент
времени ![]() . Здесь отношение
. Здесь отношение ![]() имеет смысл времени
запаздывания деформации ползучести относительно напряжения. Отношение
имеет смысл времени
запаздывания деформации ползучести относительно напряжения. Отношение ![]() тангенциального модуля
тангенциального модуля
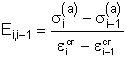 на равновесной
деформационной кривой к напряжению s входит в функцию влияния как
параметр.
на равновесной
деформационной кривой к напряжению s входит в функцию влияния как
параметр.
7. Плотность распределения элементов структуры по равновесным напряжениям
Состояние
на мезоуровне иерархической системы характеризуется плотностью распределения
элементов структуры по равновесным напряжениям ![]() , отнесенным
, отнесенным ![]() к полным напряжениям s на
макроскопическом уровне
к полным напряжениям s на
макроскопическом уровне
 (7.1)
(7.1)
Здесь ![]() ,
, ![]() ,
, ![]() ,
,![]() -величины обратные произведениям времен переходов системы из
неравновесного состояния в равновесное на b - коэффициент диффузии в фазовом
пространстве К. Постоянная С определяется из условия нормировки
-величины обратные произведениям времен переходов системы из
неравновесного состояния в равновесное на b - коэффициент диффузии в фазовом
пространстве К. Постоянная С определяется из условия нормировки
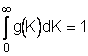 (7.2)
(7.2)
Величины параметров, входящих в
формулу (7.1), определяются по результатам макро опытов. Возможность построения
распределения элементов дискретной структуры на мезоуровне по результатам макро
опытов служит еще одним подтверждением известного принципа макро определимости,
имеющим вероятностную форму, из которой следует также определимость вероятности
разрушения.
8. Вероятности разрушения элементов структуры на мезоуровне.
Функция ![]() плотности
распределения элементов структуры по равновесным напряжениям, удовлетворяющая
стационарному уравнению Фоккера Планка
плотности
распределения элементов структуры по равновесным напряжениям, удовлетворяющая
стационарному уравнению Фоккера Планка
![]() , (8.1)
, (8.1)
определяет вероятность разрушения на мезо уровне
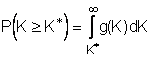 (8.2)
(8.2)
как вероятность превышения величиной
К предельно допустимого уровня ![]() .
.
9. Первичные кривые изотермической ползучести титанового сплава при
постоянных напряжениях
Первичные
кривые ползучести титанового (Ti) сплава с 6% алюминия (Al) и 4% ванадия (V) ecr измеренные при температуре 650 °С А.Д.
Расселом и А. С. Кобаяси [4], построенные на рис. 1 при трех уровнях напряжения
s1=69 МПа, s2,=131 МПа s3=172 МПа ложатся в логарифмических
координатах на прямые
![]() (9.1)
(9.1)
с наклоном b к оси ![]() и постоянной a при
заданной величине напряжения; значения коэффициентов a и b
уравнения (9.1) указаны в табл. 1.
и постоянной a при
заданной величине напряжения; значения коэффициентов a и b
уравнения (9.1) указаны в табл. 1.
Таблица 1
Значения коэффициентов уравнения (9.1) для титанового сплава
|
Напряжения, МПа |
Коэффициент a, МПа |
Показатель b |
|
69 |
0.000274 |
0.468 |
|
131 |
0.00034 |
0.625 |
|
172 |
0.000508 |
0.683 |
Из табл. 1 видно, что значения
параметров a и b зависят от уровня напряжения. В
работе [4]
принята степенная зависимость ![]()
![]() , (9.2)
, (9.2)
деформации от напряжения и времени.
Показатель степени при времени t равен постоянной величине 0.605, которая определена как
средняя величина из трех показателей степени ![]() , отличие которой от значения 0.605 составляет менее двух
процентов.
, отличие которой от значения 0.605 составляет менее двух
процентов.
10. Разделение равновесных и эффективных напряжений
Уравнение
изотермической ползучести
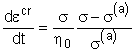 (10.1)
(10.1)
содержит две, подлежащие определению величины коэффициента
вязкости h0 и равновесного напряжения s(а), определяемых из решения системы
двух уравнений
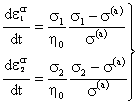 (10.2)
(10.2)
относительно равновесных напряжений
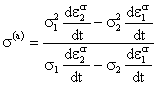 . . (10.4)
. . (10.4)
и коэффициента вязкости
 . (10.3)
. (10.3)
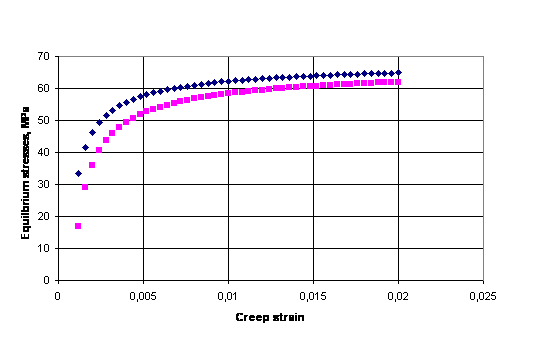
Рис. 4. Расчетные равновесные
деформационные кривые титанового сплава,
полученные с использованием формулы (10.4) для двух пар первичных кривых
ползучести.
Результаты оценки равновесных
напряжений на мезо уровне при различных деформациях для двух пар 1-3 и 1-2
первичных кривых ползучести видны на рис.4. Равновесные деформационные кривые
на рис. 4 практически совпадают между собою, что позволяет их объединить,
заменив равновесные напряжения средней величиной
![]() . (10.5)
. (10.5)
Полученная усреднением единая
равновесная деформационная кривая может быть аппроксимирована функцией (4.1)
при значениях параметров, указанных в табл. 2
Таблица 2
Значения коэффициентов равновесной деформационной кривой
(4.1)
|
|
|
A, МПа |
d |
|
|
203500 |
0.0002 |
72.43 |
0.234 |
40.7 |
Равновесная деформационная кривая
(4.1) была использована для нахождения параметров табл. 3 полилинейной
равновесной деформационной кривой (4.2).
Таблица 3
Значения равновесных
тангенциальных модулей при полилинейном деформационном упрочнении (4.2)
|
Границы участков на полилинейных
деформационных кривых (4.2) |
Равновесные напряжения, вычисленные
по формуле (4.1), МПа |
Равновесные тангенциальные модули |
|
0 |
0 |
203500 |
|
0.0002 |
40.7 |
7600 |
|
0.0025 |
58.18 |
823 |
|
0.013 |
66.82 |
401 |
|
.02 |
69.62 |
|
Представленные в табл. 3 значения
параметров равновесной деформационной кривой можно дополнить значением
коэффициентов вязкости h0 = 1200000 МПа с.
11. Ползучесть титанового
сплава при ступенчатом изменении нагрузки
Существует
точка зрения [4], согласно которой при ступенчатом изменении нагрузки теория
упрочнения лучше согласуется с данными опытов, чем теория течения. Легко
показать, что уравнения теории старения
![]() (11.1)
(11.1)
и течения
![]() (11.2)
(11.2)
являются параметрическим заданием
уравнения теории упрочнения
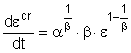 , (11.3)
, (11.3)
следовательно, обе формы задания уравнения ползучести
эквивалентны.
12. Уточненное описание
процесса ползучести титатнового сплава
Классическое уравнение
ползучести (9.2) правильно, но упрощенно описывает процесс ползучести. Точность
описания можно повысить, если воспользоваться методом изохронных деформационных
кривых Ю.Н. Работнова, предложенным еще в 1948 году [5]. Согласно этому методу
значения напряжений в фиксированные моменты времени t=20 c, 40 c,
60 c, 80 c, 100 c (изохронные сечения кривых ползучести) и соответствующие деформации
ползучести связаны между собой степенной функцией
![]() (12.1)
(12.1)
при численных значениях параметров G и g, указанных в табл. 4
Таблица 4.
Значения коэффициентов G, g уравнения изохронных деформационных
кривых (12.1) для титанового сплава
|
Время, с |
Коэффициент G, МПа |
Показатель Степени g |
|
20 |
8836 |
.704 |
|
40 |
6385 |
0.705 |
|
60 |
4071 |
0.642 |
|
80 |
2970 |
0.605 |
|
100 |
2704 |
0.6016 |
Параметры G и g уравнения (12.1), представленные в
табл. 4, могут быть записаны как функции времени
![]() (12.2)
(12.2)
![]() (12.3)
(12.3)
с коэффициентами, значения которых указаны в табл. 5
Таблица 5
Значения параметров временных зависимостей (12.2, 12.3)
коэффициентов изохронных деформационных кривых (12.1)
|
G0,МПа |
P |
g0 |
g1 |
|
11521 |
-0.0157 |
0.74 |
-.0015 |
Полученные в результате обработки
трех первичных кривых ползучести титанового сплава соотношения (12.1-12.3)
могут быть выражены одной формулой
![]() , (12.4)
, (12.4)
которая показывает, что зависимость
между напряжениями и деформациями (12.1) имеет более сложный вид
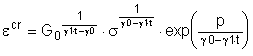 , (12.5)
, (12.5)
а принятая в технической теории
старения [4] формула (9.2), являетя ее упрощением. При подстановке t=100 в выражение (41) получим
степенную зависимость ![]() деформации ползучести
от напряжения, в которой показатель степени 1.694 всего на 2% отличается от
показателя принятого в [4]. Таким образом, упрощенная степенная зависимость
(9.2) основана на допущениях о среднем показателе степени для времени и об
использовании степенной функции напряжения с неким фиксированным показателем
степени. Этим постоянством показателей степени в классическом уравнении
ползучести объясняется различие в описании ползучести, полученном на основе
технических теорий упрочнения и течения. До внесения погрешности эти теории
были эквивалентными, а после задания в явном виде степенной функции напряжения
была внесена ошибка, которая в большей степени проявилась в теории течения по
сравнению с теорией упрочнения.
деформации ползучести
от напряжения, в которой показатель степени 1.694 всего на 2% отличается от
показателя принятого в [4]. Таким образом, упрощенная степенная зависимость
(9.2) основана на допущениях о среднем показателе степени для времени и об
использовании степенной функции напряжения с неким фиксированным показателем
степени. Этим постоянством показателей степени в классическом уравнении
ползучести объясняется различие в описании ползучести, полученном на основе
технических теорий упрочнения и течения. До внесения погрешности эти теории
были эквивалентными, а после задания в явном виде степенной функции напряжения
была внесена ошибка, которая в большей степени проявилась в теории течения по
сравнению с теорией упрочнения.
13. Ползучесть титанового сплава при ступенчатом изменении нагрузки
Расчетные
кривые ползучести при ступенчатом изменении нагрузки, построенные с
использованием коэффициентов полилинейного уравнения состояния на мезоуровне и
второго приближения к явной зависимости K(t), которые сравниваются на рис. 5 с
данными опытов [4] для титанового сплава при температуре 650°С,
показывают, что теоретическая зависимость удовлетворительно согласуется с
данными опытов.
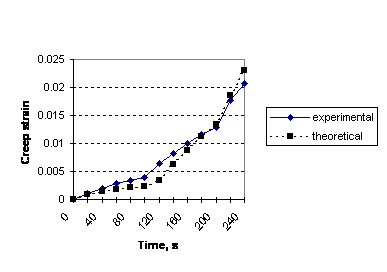
Рис. 5. Зависимости деформации
ползучести от времени при трех уровнях напряжения: 69, 131, 172 (МПа) при
температуре 650 °С.
Выводы
Гипотеза о существовании
уравнения равновесного состояния на мезоуровне дополняется гипотезой о
существовании кинетического уравнения, связывающего между собой параметры
состояния мезо и макроуровней. Для многих материалов кинетическое уравнение
можно принять в виде обобщенного уравнения Ребиндера. Для того, чтобы задать
уравнение состояния на мезоуровне, завершающего построение иерархической модели
материала (на двух уровнях) требуется отделить равновесные от эффективных
напряжений.
По методу изохронных
деформационных кривых Ю. Н. Работнова построенным по первичным кривым
ползучести удается описать ползучесть образцов титанового сплава точнее, чем с
помощью классических уравнений ползучести, за счет применения переменных
показателей степени. Уточненные изохронные деформационные кривые объясняют
наблюдаемое расхождение в описании первичных кривых ползучести с помощью теорий
течения и упрочнения, которые в действительности являются эквивалентными, в том
смысле, что они позволяют с одинаковой точностью описывать кривые
изотермической ползучести.
Для того, чтобы получить
кривую ползучести, соответствующую ступенчатому изменению нагрузки, нужно
сдвинуть верхнюю кривую (соответствующую новому возросшему уровню напряжения)
верхнюю кривую параллельно себе вниз до совпадения по деформациям.
Литература
1. Образцов И.Ф., Янковский Ю.Г. Роль
иерархического адаптивного подхода в механике гетерогенных сред. //Известия
РАН. Механика твердого тела. 1999.-№6.-95-117.
2. Ромасько В.С. Гипотеза об
универсальной форме записи конститутивных уравнений сопротивления материалов
деформации // Доповіді
НАН України. – 1997.- №5.- С.71-75.
3. Работнов Ю.Н. Ползучесть элементов
конструкций.М.: Наука. 1966.-752 с.
4. Handbook on experimental mechanics. Society for Experimental
Mechanics. Inc./Ed. by Albert S.
Kobayashi. Prentic - Hall., Inc.
5. Работнов Ю.Н. Расчет деталей машин на
ползучесть.// Известия АН СССР. Отдел технических наук. 1948-№6.-С.789 - 800 .