Samodurov A., Voronkina N.
On a mathematical model describing two processes in physics
Two physical processes, the cooperative emission on N initially inverted atoms in small sample, and the superradiance behavior of an ultrashort light pulse with a resonantly amplifying medium, are completely different. But the analytical determination of the intensity of the output pulse from both mathematical models yields ordinary differential equations of the same form.
Consider the system of N initially inverted
atoms. The followed spontaneous relaxation under some conditions yields the
output of a N-times increased compared to the ordinary fluorescence. The field
in this case is described by the system (see [1])
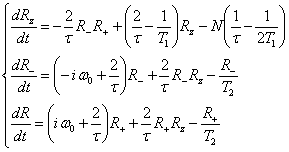(1)
where 
, 
and 
are the components of
Bloch vector, 
is the lifetime of an
isolated radioactive center, 
is a circle frequency
of the radiated field, 
is the irreversible
phase relaxation time, 
is the energy
relaxation time. The process above is known as superradiative avalanche.
According to the calculation in [1], we can
deduce from (1) that the value of the new variable X, given by 
multiplied by some
constant factor, satisfies the Coushet problem
, 
, 
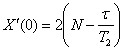(2)
The equation (2) is integrable in quadratures
only in some exceptional cases, for example when 
. In this case we can find the intensity of the output pulse
as a function of in the form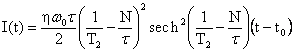 
,
where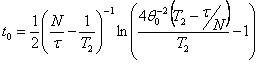 
, and 
is an initial value of
the angle of the Bloch vector.
Supperradiance is essentially the non-resonator generation of an electromagnetic field, where the inverse influence to the system is excluded. This is one of the basic conditions of the superradiative avalance [4]. Nevertheless there exists a stimulated process, where the intensity of outcoming light is proportional to the second power of the concentration of active particles. Let us look at a coherent interaction of a powerful ultrashort-wave pulse with a resonancely amplifying medium. In this case the Maxwell-Bloch system may be written as (see [5])
, 
, 
(3)
where 
, x is a space coordinate, E is the amplitude of the field, P
is the amplitude of the polarization, 
is an element of the
electric dipole moment of the particle, c is the light speed in the free of
active particles medium, 
is the pulse speed in
the medium with active particles, 
is the coefficient of
nonresonanced linear radiation losses per unit length in the medium, 
is an initial value of
population, N is the value of inverted population.
It is known [5], that under such conditions a
stationary “
-pulse” is formed. Because the difference between u and c
under additional condition 
is very small, it is
possible to propose u=c.
We will try to find a solution with constant
pulse form. That means 
. Furthermore, we have from the system (3) the “adiabatic”
connection between the polarization P and the field E, namely 
.
Using the
uniform field 
and variables 
, 
we deduce from (3) 
(4)
We can see that both the equation (2) and (4) to
be at the same form. The difference lies only in the coefficients of the
exponents. But the process described by the given equations are essentially
different.
If the solution of (4) is
.
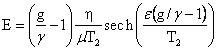The intensity of the radiance output from the
given sample is
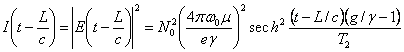(5)
The relation
(5) shows us the square dependence of the intensity and the concentrations of
sources. That was the reason for the authors [6] call the process above as
superradiance. The equation (2) and (4) lead us to investigate a more general
equation 
(6)
where 
, F(x) and f(x) are three times continuously differentiable
functions.
Theorem
1. The (6) admits a continuous group of transformations
if and only if f(x) and F(x) satisfy the relation
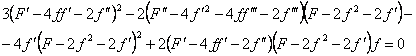(7)
It should be noted that the identity (7) is a
subject to study by itself. Being interested in physical applications we only
point out that in the general case the equation (2) and (4) both admit an
obvious continuous group of transformations 
, where 
is an arbitrary
constant. But more informative is a particular case 
.
Theorem 2 [3]. The equations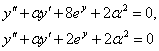 
(8)
both admit the two-parameter group of transformations
(9)
where and 
are parameters.
Corollary.
Let 
be a particular
solution of one of the equations in (8). Then the general solution of the given
equation has the form
To conclude the investigations of the equations
(8) we should note, that sometimes, knowing an admitted group of transformation
is possible to solve the equation. In our case the general solutions of the
equations (8) are the following
(10)
where M equals 2 or 8.
Now we will show a connection between the
superradiance avalanche equation and the Liouville equation. We will consider
the equation
, (11)
where
and K are non-zero
constants, and the Liouville equation
(12)
at
the same time.
Let the
functions f(x,y) and p(x,y) be two times continuously differentiable. We will
make the substitution 
, 
, 
, (13)
into the equation (12) and look for
solutions of the obtained equation not-depending on 
. Such solutions satisfy the equation 
, (14)
where subscribes denote partial derivatives.
If we require 
, 
and 
to be non-zero
constants, we have the equation in the form (11). The requirements are
satisfied, if
, 
, 
. (15)
The last equation has the general
solution (see [7])
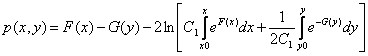(16)
where F(x) and G(y) are arbitrary
functions, is an arbitrary
constant. In view of (15) we have 
(17)
where C is an arbitrary constant.
If 
is the general
solution of the equation
, (18)
then the equation (12) has the solution
.
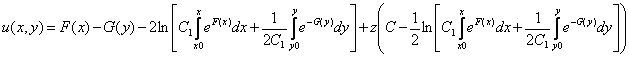The solutions of the equations (8), given by the
formula (10), look like soliton solutions under appropriate values of the
parameters at a fixed time. But this is not true. The equations (8) both have
the form (18). But all the solutions of (18) belong to the set of solutions of
the Liouville equation according to the transformation (13). It is obvious,
that the Liouville equation does not have soliton solutions (look at the
formula (16) to see that). Thus the equations in (8) admit no solutions like
soliton.
References:
1.
×óäíîâñêèé
Â.Ì., Õîëîäêåâè÷ Å.Ä. Òåîðèÿ ñâåðõèçëó÷àòåëüíûõ ëàâèí ðàäèîâîëíîâîãî äèàïàçîíà
// ÔÔÒ, 1982, òîì 24, âûï. 4, ñ. 1118-1123.
2.
Ñàìîäóðîâ
À.À., ×óäíîâñêèé Â.Ì. Î ðåøåíèÿõ îäíîãî óðàâíåíèÿ íåëèíåéíîé îïòèêè.
Äèôôåðåíöèàëüíûå óðàâíåíèÿ, 1987, òîì 23, ñ. 911-913.
3.
Ñàìîäóðîâ
À.À. Î ñâÿçè ìåæäó óðàâíåíèåì Ëèóâèëëÿ è óðàâíåíèåì ñâåðõèçëó÷àòåëüíîé ëàâèíû.
Äèôôåðåíöèàëüíûå óðàâíåíèÿ, 1989, òîì 25, ñ. 337.
4. Allen
L. and Eberly J.H. Optical resonance on two-level atoms.
5.
Êðþêîâ
Ï.Ã., Ëåòîõîâ Â.Ñ. Ðàñïðîñòðàíåíèå èìïóëüñà ñâåòà â ðåçîíàíñíî óñèëèâàþùåé
(ïîãëàùàþùåé) ñðåäå // ÓÔÍ, 1975, òîì 12, ñ. 641-672.
6. Bonifacio
R., Hopf F.A., Meystre P., Sñully M.O. Steady-state pulses and superradiance in
short-wave length swept-gain amplifiers. Phys. Rev. A., 12, 2568-2573, 1975.
7. Calogero
F. and Degasperis A. Spectral transformations and nonlinear evolution
equations. Lect. Notes in Physics 85, Springer-Verlag, 1978.