Цветков В.Н., Гейда Е.Г., Мищенко Н.В.

Днепропетровский национальный университет

ХАРАКТЕРИСТИКИ КАЧЕСТВА ТОЧЕЧНОГО ОЦЕНИВАНИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ

В общем случае точечные оценки параметров функции распределения случайного процесса являются функционалами от его реализации :

При этом идеи точечного оценивания случайных процессов являются обобщением методов построения точечных оценок значений случайных величин, а основное отличие состоит в том, что наблюдения над случайной величиной, как правило, можно обоснованно считать некоррелированными, в то время как последовательные значения временного ряда (если этот ряд не белый шум) оказываются коррелированными. При этом в зависимости от информации об априорном распределении оцениваемого параметра определяются:

– условная оценка параметра

,

которая строится по выборочным значениям в предположении, что они принадлежат распределению с фиксированным значением параметра ;

– безусловная оценка параметра

,

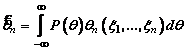получаемая усреднением условной оценки по всем возможным значениям .

Отсюда как функция случайных переменных сама оценка является случайной величиной и она должна обладать следующими свойствами, характеризующими ее качество.

Первое свойство.

Условная оценка называется несмещенной, если . При оценки называются асимптотически несмещенными. Несмещенная оценка всегда асимптотически несмещенная, но не наоборот.

Второе условие.

Условная оценка называется состоятельной, если она сходится по вероятности к оцениваемому параметру при неограниченном увеличении объема выборки , т.е. если при сколь угодно малом справедливо соотношение

.

Достаточным условием состоятельности оценки является условие

.

Третье свойство.

Условная оценка параметра называется достаточной, если для любой другой оценки условная случайная величина имеет распределение, не зависящее от . Необходимое и достаточное условие того, что была достаточной оценкой, состоит в возможности представления условной функции правдоподобия в виде произведения двух неотрицательных сомножителей:

,

первый из которых зависит от и от , а второй – только от выборочных значений и не зависит от оцениваемого параметра . Свойство достаточности оценки параметра позволяет сократить процесс накопления экспериментальных данных, необходимых для оценки параметра.

Четвертое свойство.

Условная оценка называется эффективной оценкой параметра, если при заданном смещении

.

В частности, если – несмещенная оценка, то ,

При этом отношение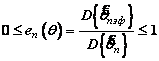

называется относительной эффективностью оценки , причем соответствует эффективной оценке. Если для данной оценки

,

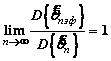то оценка называется асимптотически эффективной. Следует иметь в виду, что при сравнении двух оценок и одного параметра величина их относительной эффективности определяется как может быть любой положительной величиной.

Эффективность той или иной оценки можно оценить с помощью неравенства Рао-Крамера, которое определяет нижнюю границу дисперсий оценок и имеет вид

,

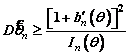откуда для оценок с постоянным смещением и для несмещенных оценок

,

где - называется информацией, содержащейся в выборке объемом .;

Это соотношение позволяет связать свойства эффективности и достаточности условных оценок: если – достаточная оценка параметра , то количество информации, содержащейся в выборке относительно параметра равно количеству информации, содержащейся в достаточной оценке , откуда получаем, что любая эффективная оценка является и достаточной (обратное утверждение в общем случае неверно).

Пятое свойство.

Из двух сравниваемых оценок и параметра назовем менее трудоемкой ту оценку, которая для достижения одинаковой точности оценок требует меньшего объема вычислений. Так как объем вычислений для построения оценок существенно зависит как от методов построения, так и от форм оценок, то этот вопрос требует отдельного рассмотрения.