К. ф.-м. н. Украинец В.Н.

Павлодарский государственный университет, Казахстан

Определение резонансных состояний неподкреплённого тоннеля при воздействии подвижной периодической нагрузки

Движущаяся вдоль тоннеля нагрузка создаёт колебания в окружающем его массиве пород, изучение которых является одной из важнейших задач механики подземных сооружений. В случае мелкого заложения тоннеля, как показано в работе [1], при достижении скорости движения периодической нагрузки скорости c_R релеевской волны стационарного решения задачи не существует: амплитуды распространяющихся вдоль земной поверхности вынужденных волн, неограниченно возрастают. При сверхрелеевской скорости движения, бегущая нагрузка генерирует распространяющиеся с релеевской скоростью незатухающие гармонические поверхностные волны с постоянной вдоль земной поверхности и экспоненциально затухающей в глубине массива амплитудой. В этом случае, кроме того, возможны резонансные состояния и для самого тоннеля (независящие от глубины его заложения), определению которых посвящена настоящая работа.

1. Рассмотрим модель неподкреплённого тоннеля в виде бесконечно длинной круговой цилиндрической полости радиусом R в линейно-упругом, однородном и изотропном полупространстве с параметрами Ламе l, m и плотностью r. Введём декартовую систему координат, ось Z которой совпадает с осью полости, параллельной свободной от нагрузок плоской границе полупространства, а ось X перпендикулярна к этой границе: x ≤ h, где h – расстояние от оси полости до границы полупространства.

По поверхности полости в направлении её оси с постоянной дозвуковой скоростью с движется периодическая по Z нагрузка

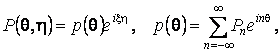
где P_j(q,h) – составляющие интенсивности нагрузки P(q,h) в подвижной цилиндрической системе координат (r,q,η = z-ct).

Граничные условия имеют вид:

- на поверхности полости

; (1)

- на поверхности полупространства

. (2)

Здесь s_ij – компоненты тензора напряжений в среде.

Выразив вектор u смещения упругой среды через потенциалы Ламе

,

представим уравнения движения среды в виде [1]

,

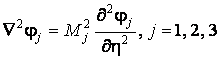где М₁ = М_p, М₂ = М₃ = М_s; M_p = c/c_p, M_s = c/c_s – числа Маха; ,  – скорости распространения волн расширения – сжатия и сдвига в среде.

Потенциалы j_j также будем искать в виде периодических функций по h

. (3)

Подставляя (3) в уравнения движения, получим

(4)

Здесь – двумерный оператор Лапласа, .

Так как скорость движения нагрузки меньше скорости распространения волн сдвига в окружающей полость среде (дозвуковая скорость), то M_s < 1 (m₂ = m₃ = m_s > 0) и решения уравнений (4) можно представить через суперпозиции поверхностных цилиндрических и плоских волн [1]

, (5)

,

,

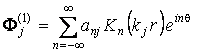Здесь K_n(k_jr) – функции Макдональда, ; g_j(x,z), a_nj – неизвестные функции и коэффициенты, подлежащие определению.

Как показано в [1], представление потенциалов в форме (5) с использованием условий (1) и (2) приводит к бесконечной системе уравнений блочно-диагонального типа с матрицами (3´3) вдоль главной диагонали

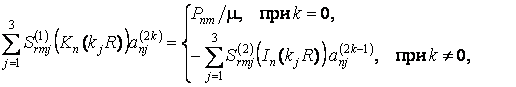(6)

; .

Вид функций и определён в [2]. Коэффициенты определяются соотношением 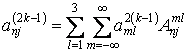. Искомые коэффициенты находятся по формуле

Система (7) имеет единственное решение, если её определитель не равен нулю. Определив коэффициенты a_nj, можно вычислить компоненты напряжённо-деформированного состояния среды.

Заметим, что рассматривая условия (6) только при k = 0 и исключая из (5) , получим решение аналогичной задачи для упругого пространства.

2. Если в уравнениях (6) отбросить правые части, то получим однородную систему линейных алгебраических уравнений, которая решает задачу о движении в тоннеле свободных поверхностных цилиндрических волн. Данная система имеет нетривиальные решения в случае, когда определитель матрицы её коэффициентов равен нулю. Из этого условия следуют дисперсионные уравнения

,

где D_n(x, с) = D_|n|(|x|, с) – определители третьего порядка на главной диагонали матрицы коэффициентов системы (6), n = 0, ± 1, ± 2, ± 3…

Дисперсионные уравнения позволяют определить точки (x_(n), c_(n)), характеризующие длину l_(n) = 2p/x_(n) и скорость c_(n) движения n-ой моды свободной волны, которая может распространяться вдоль поверхности полости.

На рис. 1 представлены дисперсионные кривые с_(n)(x_(n)) (|n|=0, 1, 2, 3, 5, 10), соответствующие уравнениям D_n(x, с) = 0. Расчёты проведены для алевролита: n = 0,2, m = 2,532×10⁹ Па, r = 2,5×10³ кг/м³, c_p = 1643,4 м/с, c_s = 1006,4 м/с, c_R = 917 м/с. Радиус полости (тоннеля) R =1 м. Здесь ярко выражено наличие горизонтальной асимптоты c = 917 м/с, которая совпадает со скоростью c_R волны Релея для данной среды. Это объясняется тем, что определитель D_n(x, с) при x ® ¥ содержит функцию Релея, которая обращается в ноль при c = c_R.

При движении периодической, с периодом по h T = 2p/x, нагрузки в неограниченном массиве со скоростью с компоненты напряжённо-деформированного состояния среды определяются однозначно, если точка с координатами (x, с) не лежит на дисперсионных кривых (в этом случае определитель системы (6) не равен нулю). В противном случае задача не имеет решения (происходит явление резонанса, перемещения и напряжения стремятся к бесконечности), хотя не исключена возможность появления множества решений, определяемых с точностью до свободных поверхностных волн в тоннеле (при этом ранг матрицы коэффициентов системы (6) должен быть равен рангу расширенной матрицы). Поэтому в дозвуковом диапазоне скоростей движения нагрузки, её параметры x и с не должны одновременно являться корнями дисперсионных уравнений, то есть следует избегать совпадения данных параметров с подобными параметрами свободных поверхностных волн в тоннеле. Отметим тот факт, что вполне допустимо совпадение частоты w = cx вынужденных колебаний массива в окрестности тоннеля с частотами w_(n) = c_(n)x_(n) собственных колебаний, то есть w = w_(n). Для этого достаточно, чтобы T ¹ l_(n) (или x ¹ x_(n)) и c ¹ c_(n). Если это условие не выполняется (x = x_(n), c = c_(n), w_* = cx, w_* = w_(n), где w_* – критическая частота) то в тоннеле возникают резонансные колебания, которые могут привести к разрушению его стенок.

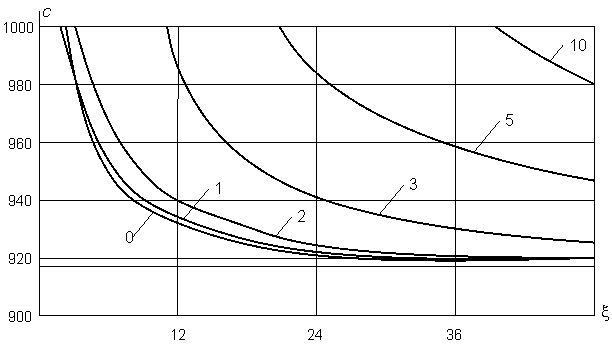
Обозначения кривых: n = 0 (0); |n| = 1 (1); |n| = 2 (2); |n| = 3 (3); |n| = 5 (5); |n| = 10 (10).

Рис. 1 – Дисперсионные кривые для неподкреплённого тоннеля

В табл. 1 приведены числовые значения частот w₍₀₎ = c₍₀₎x₍₀₎ собственных колебаний алевролита в окрестности рассматриваемого тоннеля.

Из таблицы видно, что чем больше длина свободной волны l₍₀₎ = 2p/x₍₀₎ и соответствующая ей скорость c₍₀₎, тем ниже w₍₀₎. Поэтому с увеличением скорости бегущей по тоннелю нагрузки резонансные колебания происходят при большем её периоде с понижением критической частоты w_* = w₍₀₎.

Табл. 1

c(0), м/с	920	930	940	950	960	970	980	990	1000
ξ(0), м^-1	48,8	13,4	8,1	5,9	4,7	3,8	3,2	2,7	2,3
ω(0), c^-1	44896	12462	7614	4845	4512	3886	3136	2673	2300

Приведенные рассуждения одинаково справедливы как при глубоком, так и при мелком заложении тоннеля. Однако в последнем случае, кроме того, движущаяся со сверхрелеевской скоростью нагрузка, независимо от её периода, вызывает распространяющиеся вдоль земной поверхности гармонические релеевские волны [1].

Литература:

1. Айталиев Ш.М., Алексеева Л.А., Украинец В.Н. Влияние свободной поверхности на тоннель мелкого заложения при действии подвижных нагрузок //Известия АН КазССР. Сер. физ.-матем. – 1986. – №5. – С. 75–80.

2. Украинец В.Н. О расчёте неподкреплённого тоннеля мелкого заложения при действии стационарной подвижной нагрузки //Вестник ВКГТУ. – Усть-Каменогорск, 2006. – № 2. – С.148-153.