С.А. Летучая

Днепропетровский национальный университет

Выбор рациональнойформы опор для рулонов тонколистового проката

В работе предлагается постановка и некоторые результаты решения задачи о регулировании деформированного состояния рулонов тонколистового проката путем рационального выбора формы опорной поверхности.

Хранение горячекатанного тонколистового проката в рулонах с горизонтальным расположением оси приводит к деформации его поперечного сечения. Чем больше деформация рулона, тем труднее его дальнейшее использование: при разматывании, наблюдается биение рулона, неравномерная подача и коробление листа, увеличение отходов в предстоящем раскрое. Одной из возможностей снижения материалоемкости отходов является уменьшение деформации первоначально кругового сечения за счет рационального опирания рулона. В математическом плане задача сводится к управлению распределением контактных усилий с целью оптимального нагружения конструкции. Рулон представляет собой толстостенный анизотропный цилиндр под действием собственного веса и сил взаимодействия с опорой (контактных усилий), равномерно распределенных по образующей его наружной поверхности и неравномерно в окружном направлении. 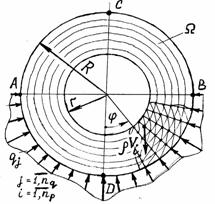В этом случае задача сводится к исследованию плоскодеформированного состояния изолированного кольца единичной длины, выделенного из рулона двумя поперечными сечениями. На рис. 1. изображена расчетная схема задачи, где , – внутренний и наружный радиусы кольца; – контактное усилие в -той точке предполагаемой площадки контакта, первоначально органиченной максимальным углом охвата a=180°; – количество точек контакта; – количество узлов конечных элементов. Характеристики анизотропного материала кольца задаются по результатам экспериментов [1], полученных с учетом количества витков рулона, толщины листа, температуры и марки стали ; ; , где – модуль упругости материала кольца в окружном и радиальном направлениях. Вектор внешней нагрузки составляют приведенные в узлы конечных элементов массовые усилия:
, где – плотность материала; – объем.

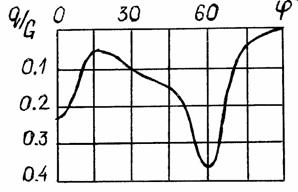
Рис. 1. Расчетная схема задачи Рис. 2. Распределение контактных усилий

О величине деформации кольца можно судить по разности перемещений диаметрально противоположных точек, например и , и :

, где и .

Задачу поиска распределения контактных усилий оптимального с точки зрения уменьшения деформации поперечного сечения кольца можно сформулировать следующим образом: в -мерном пространстве проектирования найти допустимую точку , в которой выполняется условие , (1)

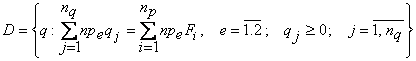(2)

где – множество допустимых решений; – область дискретизации анизотронного кольца; – поекция на оси координат ; – условие односторонней связи кольца и опоры.

Сформулированная задача представляет собой задачу нелинейного программирования с функцией цели (1) и ограничениями типа равенств и неравенств (2), накладываемых на вектор проектных параметров. Решение оптимизационной задачи осуществляется с использованием метода деформируемого многогранника, определение напряженно-деформированного состояния кольца – с использованием метода конечных элементов. На рис. 2 представлено распределение ( – собственный вес кольца), полученное в результате решения задачи (1) – (2), где максимальные величины соответствуют узлам с угловыми координатами 0° и ±60°. 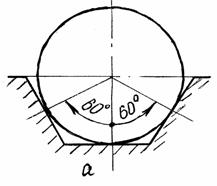Зная, что в соответствии с технологическим процессом рулонам горячекатанного проката необходимо обеспечить условия охлаждения, приближающиеся к всестороннему и равномерному, представляется целесообразным предложить опирание в 3-х точках, которое может обеспечить ложемент, изображенный на рис. 3,а. Для кольца и ложемента, предложеной конфигурации, была решена контактная задача с использованием алгоритма описанного в [2,3]. Отклонение величины , полученной в результате решения контактной задачи, от величины , полученной в задаче (1)-(2), составило 15,7%.

Рис. 3. Рациональная форма

опорной поверхности

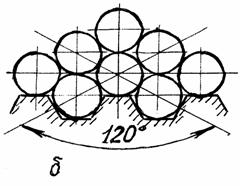
При многослойном хранении рулонов предлагается использовать условия опирания, изображенные на рис. 3,б. В этом случае каждый рулон будет опираться в 3-х точках, угловые координаты которых 0°, 60°, -60°.

ЛИТЕРАТУРА

1. Пелех Б.Л., Сухорольский М.А. Контактные задачи теории упругих антизотронных оболочек. Киев: Наук. думка, 1980. – 214 с.

2. Бинкевич Е.В., Летучая С.А. Контактная задача для кольца и упругого ложемента. // Прикладная механика. – 1984. – № 10. – С. 79-84.

3. Летучая С.А. Оптимизация распределения реакций взаимодействия. – Вісник НДУ. Сер. Ракетно-космічна техніка. – 1997. – Вип. 3. – С. 82-84.