Н. Н. Убизький, А. Г. Фесенко
Днепропетровский национальный университет
УСТОЙЧИВОСТЬ
ТОНКИХ СТЕНОК ПРОФИЛЕЙ ПРИ ИЗГИБЕ
Рассмотрим устойчивость цилиндрических и конических
стенок, расположенных в зоне сжимающих тангенциальных деформаций. При
определенном соотношении геометрических размеров, механических характеристик
материала и кривизны нейтрального слоя профиля стенки теряют устойчивость с
появлением гофров, имеющих определенную длину полуволны а
и максимальный прогиб при выпучивании w
. Тонкую стенку с размерами поперечного
сечения a и d (
-угол наклона конической стенки), можно рассматривать как
оболочку.
Задача определения критического радиуса кривизны при
местной потере устойчивости цилиндрических и конических стенок, которые
находятся в условиях линейного напряженного состояния (
), решается в соответствии с методом, разработанным С. П.
Тимошенко [1] и распространенным на
задачи устойчивости за пределом
упругости
А. А. Ильюшиным [2]. Согласно энергетическому критерию устойчивости
уравнение критического состояния равновесия имеет вид:
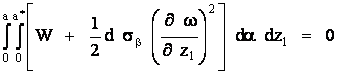(1)
где: W - потенциал изгибающих и крутящего
моментов, обусловленных образованием гофров в результате потери устойчивости; 
- функция,
аппроксимирующая форму гофров; a* - длина полуволны; 0z
- ось, совпадающая с направлением
касательной к оси 
.
Граничные условия для функции прогиба w имеют следующий вид:
w = 0 при
a = z = 0.
(2)
В уравнении критического состояния (1) принимаем функцию,
аппроксимирующую форму волны и
удовлетворяющую граничным
условиям (2), в следующем виде: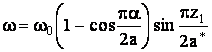 
.
Напряженное
состояние, предшествующее моменту потери устойчивости, принимаем линейным.
Величина относительной тангенциальной деформации в условиях линейного
напряженного состояния равна 
, где h - расстояние от нейтральной линии.
Кривая
упрочнения принята в виде 
.
Потенциал
изгибающих и крутящих моментов из (1), обусловленных горообразованием,
определяется по формуле [2]:
W = 
E
I 
,
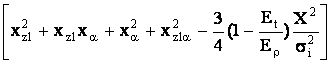(3)
где I – момент инерции полоски единичной длины, вырезанной из
исследуемой стенки; E - модуль пластичности; Е
- касательный модуль; 
, 
, 
- вторые частные производные от функции прогиба w
по соответствующим переменным; X= 
; 
- тангенциальное
напряжение.
Учитывая линейный характер напряженного состояния, имеем
e
= 
; |
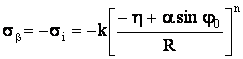. (4)
Подставляя
выражения (3)- по (4) в уравнение критического состояния равновесия (1), беря
частные производные и вычисляя определенные интегралы, находим выражения для
радиуса кривизны нейтрального слоя профильной заготовки
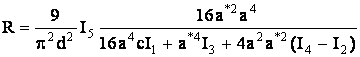, (5)
где:
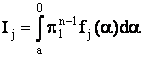, при
j = 1,2,3,4,5;
; 
; 
;
; 
;
; 
; 
.
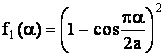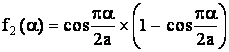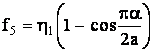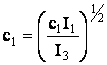Находим экстремум функции 
из условия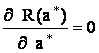 
.
Окончательно,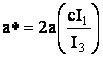 
и 
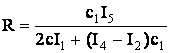, (6)
где: 
- максимальный радиус кривизны, при котором происходит
местная потеря устойчивости стенок профиля.
Для расчета
критического радиуса кривизны и длины полуволны по формулам составлен алгоритм
решения и программа. Исходными данными
являются геометрические
характеристики профиля: а, d, (- угол наклона тонкой стенки), а также А и показатель степени
n в выражении для кривой
упрочнения. Интегралы 
, входящие в выражения (5) и (6), вычислялись численно с
помощью стандартных программ, реализующих вычисления определенного интеграла по
квадратурной формуле Гаусса с десятью узлами.
В том
случае, когда значения критического радиуса больше, чем радиус гибки,
рекомендуется выбрать другой тип профиля или при проектировании
технологического маршрута изготовления своевременно предусмотреть калибровку в
штампе для устранения гофров, образующихся при местной потере устойчивости.
Библиографические
ссылки
1. Тимошенко С. П. Устойчивость
стержней, пластин и оболочек. - М.: Наука, 1971. – 807 с., ил.
2. Ильюшин А. А. Пластичность. - М.: ГИТЛ, 1948.
– 376 с., ил.