Радкевич А.В., Яковлев С.А., Бондаренко Л.Н., Гуменюк В.Е.

Днепропетровский национальный университет железнодорожного транспорта им. В. Лазаряна .

Усилия и напряжения в разномодульных стержнях в жидкости.

Практически всем материалам в той или иной степени присуща разномодульность. Явление разномодульности установлено для многих сталей и сплавов [1]. Например, отношения модуля упругости при одноосном растяжении (Е⁺) к модулю упругости при сжатии (Е^–-) составляют: для стали 40 нормальной 0,97; для стали У8 нормальной 0,96; силумина АП2 0,91 и т.д. Еще большей разномодульностью обладают композиционные материалы, боропластики, конструкционные граниты и т.п. детали и изделия из которых часто работают в различных жидкостях.

Неучет разномодульности может привести к существенным погрешностям при расчете напряжений в конструкциях.

Некоторые задачи одноосного растяжения – сжатия вертикальных стержней не погруженных в жидкость приведены в работе [1].

В общем случае напряжения по длине стержня меняют знак. Поэтому необходимо найти координату плоскости разделения напряжений и напряжения в любой точке стержня любой площади поперечного сечения.

Таким образом, установить как влияет угол наклона стержня и плотность жидкости на величину координаты, где напряжению меняют знак и на сами напряжения одноосного растяжения – сжатия.

Приведем решение задач одноосного растяжения – сжатия наклонны или вертикальных стержней погруженных в жидкость при характерных различных расчетных схемах нагружения и закрепления краев.

А. Пусть наклонный под углом α к горизонту стержень длиной ℓ плотностью γ погружен в жидкость плотностью γ’ (рис.1). При этом нижний конец (х = 0) закреплен жестко, а к свободному верхнему концу (х = ℓ) центрально приложена растягивающая сила Р.

В общем случае напряжения по длине стержня меняют знак. Поэтому, необходимо найти координату плоскости разделения напряжений и напряжения в любой точке стержня площадью сечения F.

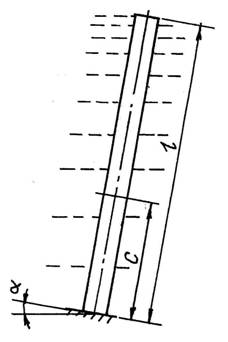
Рис.1. Расчетная схема стержня, погруженного в жидкость, с нижним жестко закрепленным концом.

Граничные условия задачи запишутся в виде

u = 0, при х = 0; , при х = ℓ (1)

Уравнение равновесия имеет вид

(2)

Определив постоянную интегрирования, получим для напряжения

(3)

из последнего выражения можно заключить, что при Р = 0, в зависимости от конкретных значений γ и γ’, стержень может быть или полностью сжат или же полностью растянут: при стержень полностью растянут.

Координату плоскости разделения напряжений можно найти, прияв из (2):

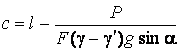(4)

Обобщенный закон упругости имеет вид:

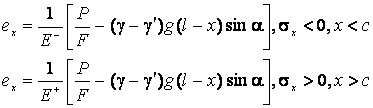(5)

Имея в виду, что U = U₁(x) на участке 0 ≤ x ≤ c, преобразуем соотношение (5) к виду

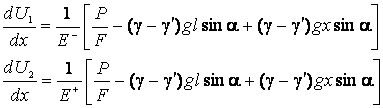(6)

Отсюда имеем

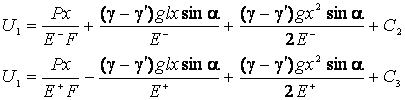(7)

Б. Рассмотрим наклонный стержень в жидкости с двумя жестко закрепленными концами, находящийся только под действием только собственного веса.

Граничные условия имеют вид:

u = 0, при х = ℓ; u = 0, при х = ℓ; (8)

Уравнение равновесия стержня запишется так:

(9)

Для сжатого и растянутого участков стержня обобщенный закон упругости запишется в виде:

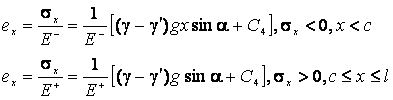(10)

Аналогично предыдущей задаче, перепишем последнее уравнение следующим образом:

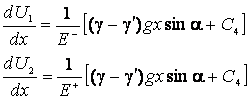(11)

Имея граничные условия (8) и условие непрерывности на плоскости контакта двух участков стержня, запишем выражение для двух перемещений на участках 1 и 2:

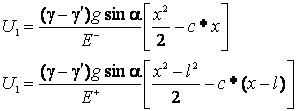(12)

где

В. В случае, когда один конец стержня, находящийся на поверхности жидкости, жестко закреплен, а второй свободен, в формулах (9)–(12) перед необходимо поменять знак на обратный.

В качестве примера для трех приведенных случаев рассмотрим стальную трубу погруженную в жидкости разной плотности. Материал трубы сталь 40 с , , , нагружаемым диаметром , толщиной стенки , длиной и приведенной плотностью . Плотность жидкости . Рассмотрим случаи, когда труба заполнена жидкостью плотностью, равной плотности окружающей трубу жидкости и не заполненной.

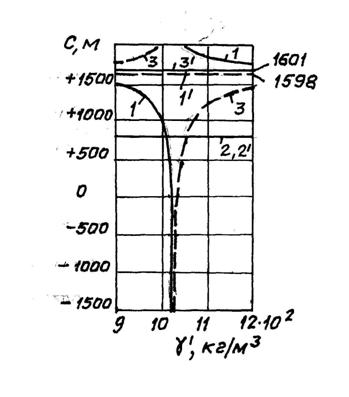
Рис.2. зависимость координат плоскости разделения напряжений от плотности жидкости. 1 – случай А для незаполненной жидкостью трубы; 2 – тоже для случая Б; 3 – тоже для случая В; 1,2,3 – заполненная жидкостью труба для случаев А,Б,В соответственно.

Анализ формул и графиков, представленных на рисунке 2 позволяет сделать следующие выводы:

- Углы наклона и плотность жидкости в которую погружен стержень оказывают существенное влияние на величины координат, где напряжение меняет знак и на сами напряжения одноосного растяжения–сжатия;

- Разномодульность материала может, в зависимости от соотношения модулей упругости, при растяжении и сжатии, оказывать существенное влияние на напряжения в стержне;

- Угол наклона стержня, плотность жидкости и разномодульность должны учитываться при расчете длинных стержней.

Литература

1. Амбарцумян С.А. Разномодульная теория упругости. –М.:наука,1982.–320 с.