Виноградова И.М.

Барановичский государственный университет, Беларусь

Статистическое моделирование процессов в системах массового обслуживания

Модели системы массового обслуживания являются наиболее часто используемым классом моделей со случайными факторами, что определяется повсеместным распространением систем такого типа.

К настоящему времени разработано много моделей систем массового обслуживания, имеющих аналитическое решение. Но они далеко не исчерпывают все способы функционирования реальных обслуживающих систем. Кроме того, на практике не всегда выполняются предпосылки, лежащие в основе имеющихся аналитических моделей.

Эффективным методом решения задач теории массового обслуживания, как и многих других, не имеющих аналитического решения, является метод статистического моделирования, предусматривающий, имитацию на ЭВМ процессов, протекающих в исследуемой системе. Математическое описание процесса в этом случае задается алгоритмически. Моделирующий алгоритм многократно воспроизводит изучаемый случайный процесс, накапливает сведения о его протекании, и после обработки выдает оценки показателей работы системы. Автором разработана имитационная модель, для исследования состояния очередей в одноканальной и многоканальной системах массового обслуживания. Целью любого компьютерного эксперимента является сбор информации о значениях переменных модели, наблюдаемых в процессе проведения эксперимента, и состояниях очередей, возникающих в процессе моделирования.

Рассматривалась следующая постановка задачи:

На вход n-канальной системы массового обслуживания поступает ординарный стационарный поток однородных событий с ограниченным последействием и заданным распределением F1(t) промежутков времени t между моментами поступления последовательных требований. Если в момент появления требования имеются свободные каналы, обслуживание начинается немедленно тем из них, который свободен дольше других. Если все каналы заняты, требование ставится в очередь и попадает на обслуживание после всех требований,пришедших ранее.Время обслуживния T – случайная величина с известным для каждого канала распределением F2(t). Количество источников требований, длина очереди и время ожидания или пребывания в системе не ограничено. Требуется определить характеристики работы системы:

k - коэффициент простоя канала

М₁ - среднюю длину очереди

М - среднее число требований в системе

w - средние потери времени на ожидание одним требованием начала обслуживания.

В практических задачах, связанных с изучением входящего потока требований, удобно вместо распределения числа требований k по отрезкам времени t исследовать распределение интервалов времени между появлениями соседних требований. Вероятность того, что на участке времени t, следующем за моментом поступления одного из требований, не появится ни одного требования, в соответствии с законом Пуассона [1] находиться по формуле (1).

(1)

Но эта вероятность (2) равна вероятности того, что случайная величина будет не меньше величины t .

, (2)

(3)

Функция распределения случайной величины выражается по формуле (3). Дифференцируя это выражение, получаем плотность распределения случайной величины формула (4).

(4)

Таким образом, в пуассоновском потоке интервал времени между любыми двумя соседними требованиями подчиняется экспоненциальному (показательному) распределению с параметром .

Время обслуживания является важнейшей характеристикой каждого обслуживающего прибора, определяющей пропускную способность системы массового обслуживания. Как правило, время обслуживания — случайная величина. Причина этого нестабильность работы обслуживающих приборов, неидентичность поступающих в систему требований. Исчерпывающей характеристикой времени обслуживания Т, как и любой другой случайной величины, является его функция распределения F(t)=P(T<t). Следует отметить, что большинство аналитических результатов в теории массового обслуживания получено в предположении, что время обслуживания имеет экспоненциальное распределение (5).

(5)

Параметр называется интенсивностью обслуживания и имеет простой физический смысл. Это величина, обратная среднему времени обслуживания одного требования:

Та большая роль, которую играет экспоненциальное распределение времени обслуживания в теории массового обслуживания, связана с одним его важным свойством. А именно, если в какой-либо момент происходит обслуживание требования, то распределение оставшегося времени обслуживания не зависит от того, сколько времени обслуживание уже продолжалось.

Пусть есть вероятность того, что обслуживание, которое уже продолжалось время α, продлится еще не менее t . В частном случае означает вероятность того, что начинающееся обслуживание продлится не менее t (6). Аналогично и для формула (7).

(6)

(7)

В то же время по теореме умножения вероятностей можно рассчитать как произведение вероятности того, что обслуживание продлится не меньше, чем α, на вероятность того, что, продлившись в течение времени α, оно продлится еще не менее t – формула (8). Переходя к явным выражением, получаем формулу (9), откуда находим, что равно - формула (10), что и требовалось доказать [1].

(8)

(9)

(10)

Составлен проект в среде Delphi c использованием датчика случайных чисел. В диалоговом окне формы проекта (рис.1.) «Расчетные значения» - это результаты аналитического расчета коэффициента простоя канала k, среднего времени ожидания требованием начала обслуживания w, средней длины очереди М1 по формулам (11)-(13) при показательных законах распределения времени между последовательными требованиями входящего потока [1].

; (11)

; (12)

. (13)

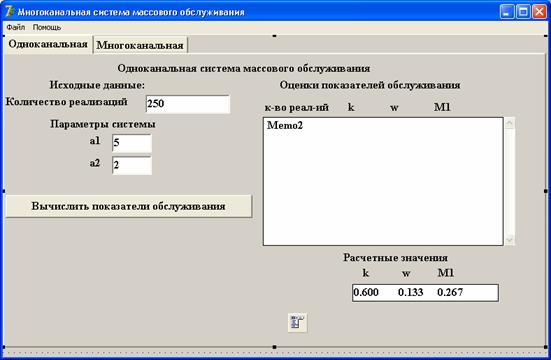
Рисунок 1 – Диалоговое окно 1

В одноканальной системе отсчет времени начинался для каждого нового требования с момента его поступления и заканчивался в момент завершения обслуживания. Моделирование процесса производилось при значениях параметров n=3, λ=2, μ=5 и при показательных законах распределения F1(t) интервалов между последовательными требованиями входящего потока и F2(t) времени обслуживания.

В таблице 1 представлены результаты моделирования одноканальной системы массового обслуживания при различном числе реализаций процесса обслуживания, при этом результаты аналитического решения и статистического моделирования достаточно близки между собой.

Таблица 1. Характеристики одноканальной системы.

Количество реализаций	Оценки показателей обслуживания одноканальной системы
Количество реализаций	k	w
250 500 1000 2000 4000 8000 16000	0,581 0,580 0,576 0,587 0,597 0,598 0,600	0,122 0,151 0,141 0,120 0,134 0,126 0,125	0,240 0,294 0,283 0,238 0,262 0,253 0,250
Расчетные значения	0,600	0,133	0,267

При оценке работы многоканальной системы массового обслуживания, вводится новый параметр (рисунок 2), характеризующий данную систему: среднее число требований в системе (M).

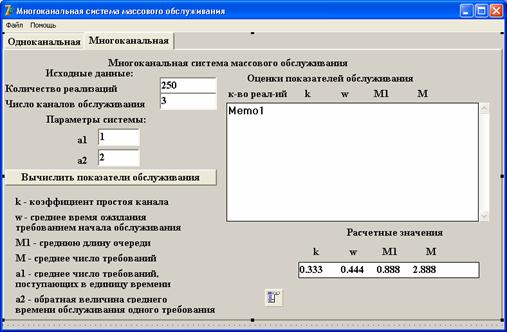
Рисунок 2 - Диалоговое окно 2

В многоканальной системе время наблюдения изменяется интервалом от момента поступления первого требования до момента завершения обслуживания последнего из общего числа требований. В таблице 2 приведены результаты моделирования при значениях параметров n=3, λ=2, μ=1 и при показательных законах распределения F₁(t) интервалов между последовательнымитребованиями входящего потока и F₂(t) времени обслуживания.

Таблица 2. Характеристики многоканальной системы.

Количество реализаций	Оценки показателей обслуживания многоканальной системы
Количество реализаций	k	w	M ₁	M
250 500 1000 2000 4000 8000 16000	0,351 0,301 0,296 0,313 0,328 0,330 0,332	0,460 1,123 0,743 0,515 0,483 0,432 0,422	0,916 2,189 1,493 1,024 0,647 0,866 0,843	3,037 4,288 3,613 3,091 2,965 2,877 2,846
Расчетные значения	0,333	0,444	0,889	2,846

Программа может быть использована для исследования состояний подобных моделей при изучении имитационных процессов систем массового обслуживания.

Результаты моделирования при различном числе реализаций процесса обслуживания показали, что результаты аналитического решения и статистического моделирования достаточно близки между собой. Модели системы массового обслуживания являются наиболее часто используемым классом моделей со случайными факторами, что определяется повсеместным распространением систем такого типа.

Литература:

1. Балашевич В.А. Андронов А.М. Экономико-математическое моделирование производственных систем: Учебное пособие для вузов.- Мн: Унiверсiтэцкае,1995,-240 c.