Физика

К.т.н. Орлов П.С.

ФГОУ ВПО «Ярославская государственная сельскохозяйственная

академия»

Уточнение механизма образования молекулярной связи

При климатических температурах водород – бесцветный газ без запаха. При температуре ниже 33 [К] под давлением водород может быть превращен в бесцветную жидкость, кипящую при температуре 20,2 [К]. Если быстро испарять жидкий водород – получится твердый водород в виде прозрачных кристаллов плавящихся при температуре 13,8 [К]. При высокой температуре молекулы водорода диссоциируют на атомы с поглощением большого количества тепла:

H₂ « 2Н + 453,6 [кДж / моль]. (1)

Реакция обратима и сдвигается вправо при повышении температуры. При 2273 [К] количество диссоциировавших молекул водорода составляет только 0,1 %. При 3273 [К] количество диссоциировавших молекул водорода повышается до 9%. При 4273 [К] диссоциирует 62,5 % молекул, а при 6273 [К] диссоциирует 94,7 % молекул – диссоциация становится почти полной [1]. Атомарный водород, образующийся при давлении порядка 0,5 мм ртутного столба действием на водород тлеющего разряда, не сразу объединяется обратно в молекулы. Атомы водорода гораздо активнее молекул. Для вступления в реакцию молекулы водорода должны сначала диссоциировать на атомы, для чего необходимо затратить большое количество энергии. Тепло, затраченное на разложение молекул водорода выделяется обратно, когда эти атомы воссоединяются в молекулы. На диссоциацию одной молекулы водорода затрачивается 4,7 [эВ].

Если сближать два атома водорода, находящихся на значительном расстоянии друг от друга, то с расстояния L = (8 ÷ 10)r_B атомы «замечают» друг друга, так как вращающийся вокруг протона электрон представляет собой виток тока, создающий магнитный поток Ф. Два магнитных потока, взаимодействуя друг с другом, ориентируются таким образом, что «стягивают» протоны, образуя четырехмассовую систему. При расстояниях между протонами меньше двух боровских радиусов r_B электроны уходят в потенциальную «яму» - кроме вращения вокруг своих протонов, начинают обращаться вокруг общего центра масс системы. Минимуму потенциальной энергии системы соответствует состояние, когда два протона и два электрона образуют плоский квадрат. Любое изменение их пространственного положения ведет к тому, что уменьшается одна из диагоналей, а вторая удлиняется. В результате нелинейно изменяются силы отталкивания: увеличиваясь вдоль укорачивающейся диагонали, и уменьшаясь вдоль удлиняющейся. Одновременно растут силы притяжения вдоль удлиняющейся диагонали и падают вдоль укорачивающейся. Расстояние между любым электроном и любым протоном строго нормировано радиусом Бора. Потенциальная энергия системы этих атомов (сумма энергий отталкивания протонов и электронов и энергии притяжения любого из электронов с любым из протонов) в состоянии равновесия равна:

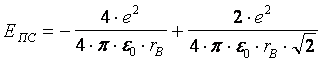. ( 9)

Кинетическая энергия системы равна удвоенной кинетической энергии одного атома водорода плюс кинетическая энергия обращения атомов водорода вокруг общего центра масс – в той части объема молекулы, где образуется повышенная электронная плотность. Полная энергия системы будет:

(10)

Минимуму на кривой изменения потенциальной энергии системы из двух атомов соответствует перекрытие 1s атомной орбитали с образованием повышенной электронной плотности между двумя протонами – получаем двухатомную модель вещества Я.И.Френкеля [2].

Уменьшение величины энергии четырехмассовой системы продолжается, пока расстояние между атомами водорода Н - Н не станет равным межъядерному расстоянию: R_Z=L₀=2^1/2r_B = 74,9533 [пм] (справочные данные [3] – 74,14 [пм] ), что соответствует значению энергии связи двухатомной системы, равному:

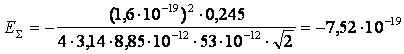[Дж] =

= -7,52·10^-19·0,624·10¹⁹= - 4,693 [эВ],

или, в пересчете на моль вещества:

Е_ПСМ=Е_ПС·N_A= -7,52·10^-19·6,0225·10²³ = - 452892 [Дж/моль];

(справочное [3] значение – 453,6 [кДж/моль] ).

По И.Е. Тамму взаимодействующий атом не может отдать на молекулярную связь более половины своей собственной энергии [4]. Для водорода это:

W_C £ - 13, 55/2 = - 6,78 [ эВ ] ,

что соответствует расчетам (10): W_C(Н-Н) = - 4,7 [ эВ ].

Первый радиус Бора электрона атома водорода определяется не только Кулоновским взаимодействием зарядов ядра атома (протона) и электрона и скоростью движения электрона по орбите, но и взаимодействием магнитного поля протона и вращающегося вокруг него электрона. Так как радиус протона [5] с присущим ему пионным (π-мезонным) облаком составляет порядка радиуса классического электрона:

R_П = 1,5 · 10^-15 · А ^1/3 = 1,5 · 10^-15 [ м ],

где А - число нуклонов в ядре,

(что почти на 4 порядка меньше первого радиуса Бора, равного R_В = 5,29171 · 10^-11 [ м ] ), то плотность энергии магнитного потока ядра протона (образуемого вращением заряда протона) на 8 порядков выше плотности энергии магнитного потока электрона находящегося на первом Боровском радиусе. Так как взаимодействие нуклонов в ядре атома осуществляется на очень малых расстояниях порядка:

R_Я = h / 2π · m(π) · c = 1,2 · 10^-15 [м],

где m(π) - масса π - мезона,

то силы магнитного взаимодействия нуклонов вносят значительный вклад не только в силы ядерного взаимодействия, но и определенный вклад в силы межъядерного взаимодействия в молекулах. В итоге, каждый из нуклонов ядра атома представляет собой магнит. Равновесие системы, состоящей из нескольких магнитов (нуклонов), может сохраняться только в том случае, если магнитные поля двух взаимодействующих частиц направлены либо в одну сторону, либо – в противоположных направлениях. В первом случае плоскости вращения зарядов в нуклонах нормальны одной оси. Во втором случае нормали плоскостей параллельны. В ядре атома гелия два протона и два нейтрона. Они соединяются (сшиваются) магнитными полями нуклонов попарно цепочкой протон – нейтрон. При этом нуклоны одной пары нейтрон – протон располагаются на одной нормали к площади поперечного сечения их совместного магнитного потока, а вторая такая же пара расположена на параллельной нормали и ее совместный магнитный поток направлен в обратную сторону. Вследствие этого два параллельных магнитных потока замыкаются своими полюсами по кольцу: -N-S-N-S- . В результате суммарный магнитный поток ядра атома гелия равен нулю. Именно поэтому атомы гелия не объединяются в молекулы, так как отсутствует взаимодействие магнитных полей двух соседних ядер.

Основное отличие атомарного газа от молекулярного связано с существованием у молекул (кроме трех поступательных ) колебательной и двух вращательных степеней свободы. И если энергия, затрачиваемая на вращательную степень свободы невелика и не превышает нескольких тысячных электрон-вольт (что соответствует повышению температуры на десятки градусов), то энергия колебательного движения большинства газов составляет десятые доли эВ, что эквивалентно нагреву на несколько тысяч градусов .

Средняя кинетическая энергия поступательного движения молекул идеального газа (как материальной точки, имеющей три степени свободы), выражается через термодинамическую температуру:

W_К =3kT/2, (11)

- при нормальных температурах кинетическая энергия молекулы идеального газа в 50 … 30 раз больше, чем при температурах 4 … 5 [К]. На одну степень свободы поступательного движения атома приходится:

W₀ =kT/2, (12)

- образование молекулы оказывается энергетически выгодным, так как каждый из атомов имеет три степени свободы (в сумме 6 степеней своды), а молекула, состоящая из двух объединившихся атомов, при температурах порядка 300 [К] имеет 3 поступательные степени свободы и 2 вращательные.

При нагревании на 1 градус Кельвина прирост энергии поступательного движения DW_П1 на каждую степень свободы составляет:

DW_П1 = [k (T +1) / 2] - k · T / 2 = k / 2 = 0,69027·10 ^–23 [ Дж / К ] =

= 0,69027·10 ^–23 · 0,624·10 ¹⁹ = 0,43·10^–4 [ эВ / К ].

В соответствии с квантовой механикой вращательная энергия молекул изменяется не непрерывно, а квантами. При температурах близких к нормальным квант энергии вращательного движения мал, по сравнению с W₀ = kT/2. При низких температурах многоатомные (двухатомные) молекулы практически перестают вращаться и движутся только поступательно - «вымерзают» вращательные степени свободы. Энергия колебательной степени свободы (атомов в молекуле относительно друг друга) также квантуется. При низких и близких к нормальным температурах кванты колебательной степени свободы значительно больше W₀ = kT/2, поэтому при столкновениях молекул их атомы не приходят в колебательный процесс – колебательная степень свободы не возбуждается.

Молекула является квантовой системой, описываемой уравнением Шредингера. Энергия изолирований молекулы Е_М учитывающая энергию Е_Е движения электронов в атомах и в молекуле, колебания атомов Е_К в молекуле, энергию вращения Е_В молекулы и ее поступательного движения Е_Д описывается уравнением:

Е_М @ Е_Е + Е_К + Е_В + Е_Д. (13)

Приведенное выражение (13) не учитывает энергию ядер атомов. Энергия поступательного движения молекул не квантуется, поэтому не приводит к образованию молекулярного спектра. Отношение энергий [6] имеет вид:

Е_Е : Е_К : Е_В = 1 : (m_E / М)^1/2 : m_E / М @

@ (1 ÷ 10 ) [ эВ ] : (10 ^{– 2} ÷ 10 ^{– 1} ) [ эВ ] : (10 ^{– 5} ÷ 10 ^{– 3} ) [ эВ ],

где М - масса ядер в молекуле.

Следует отметить, что радиус атома водорода, в соответствии со справочными данными [3], несколько больше радиуса Боровской орбитали и составляет: R_Н = 78 [пм]. Это кажущееся противоречие разрешается Вихмановской моделью электрона, по которой электрон m_Е - суть внутренняя масса (керн) электрона mi, окруженная электромагнитной оболочкой me; по Э. Вихману [7]:

m_Е = mi + me . (4)

В соответствии с физической электромагнитной моделью молекулы, предложенной В.П. Гусевым [8, 9], заданная положением электрона в атоме электромагнитная компонента его массы me генерируется зарядом электрона из его массы покоя и воплощается в витке тока, окружающем внутреннюю массу электрона (керн) mi. При вращении витка вокруг оси, проходящей через mi, образуется шаровой конденсатор. В соответствии с этой моделью радиус электромагнитной оболочки электрона R_Е - его электромагнитной компоненты mе, сопоставим с радиусом орбитали электрона и только немногим меньше радиуса Бора: R_В >@ R_Е .

Максимальный расчетный диаметр атома водорода D_НМАХ (по справочным [10] данным 154 [пм] ) будет:

D_НМАХ = 2R_В + R_Е @ 3R_В = 158,4 [пм], (5)

а радиус атома водорода:

R_Н @ D_НМАХ / 2 = 3R_В / 2 = 79,2 [пм], (6)

что с точностью до 1,54 % cоответствует справочным данным [3].

Учитывая опытные данные [3] о размере атома водорода R_Н = 78 [пм], рассчитаем [11] уточненный радиус электромагнитной оболочки электрона:

R_Е0 = 2R_Н - 2R_В = 2 · 78 - 2 · 52,8 = 50,4 [пм]. (7)

Следует отметить, что справочные данные [12] радиуса атома водорода по Медини – Хьюзу (37,07 [пм]) и Полингу (31 [пм]), значительно меньше Боровского радиуса, и являются, вероятнее всего, значением примерно половины расстояния между протонами (ядрами атомов) в молекуле водорода, так как атом водорода несжимаем, а минимальный радиус орбитали атома водорода - Боровский.

В соответствии с идеей Э. Вихмана, согласно которой масса покоя электрона m_Е [7] двухкомпонентна и включает в себя внутреннюю массу (керн) электрона mi, окруженную электромагнитной оболочкой me, представляющую электромагнитную составляющую энергии электрона: m_Е = mi + me. Эта составляющая может быть представлена в двух энергетически адекватных состояниях: круговым витком тока [9], образуемого вращающимся вокруг керна электрона (центра тяжести массы электрона) его заряда; или шаром, образованным вращением этого витка вокруг оси, проходящей через центр тяжести внутренней массы электронов. Электростатическая энергия конденсатора определяется выражением:

W = е ² / 2С (8)

где: С - емкость конденсатора [Ф], равная в системе Гаусса радиусу шара: С = R [cм]; 1 [cм] = 1,1125 · 10 ^-12 [Ф]; 1 [м] = 1,1125 · 10 ^-10 [Ф].

В основном (не возбужденном) состоянии атома водорода масса электрона

(его керн) располагается в любой точке поверхности сферы первого Боровского радиуса, а заряд электрона (в основном состоянии) располагается на поверхности сферы электромагнитной оболочки электрона, радиус которой близок к радиусу орбитали электрона. Величина электромагнитной энергии электрона при нахождении его на первом Боровском радиусе [12]:

r_В = (h ² · e₀) / ( p · m_Е · е ² ) @ k_В / a = 52,9171 · 10 ^-12 [м]

в соответствии с выражением (8) равна [12, 5]:

W = е ² / 2С = (1,6 10 ^-19 ) ² / 2 · ( 52,9171 · 10 ^-12 ) · 1,1125 · 10 ^-10 =

= 2, 177 · 10 ^-18 [ Дж ] = 2, 177 · 10 ^-18 · 0,624 · 10 ¹⁹ = 13,59 [эВ] ;

где 1 [Дж] = 0,624 · 10 ¹⁹ [эВ] ;

h = 6,6256 · 10 ^-34 [ Дж · с ] - постоянная Планка;

a = ( е ^{2 )} / 2h · с · e₀ = | [(2R_Y · h ) / ( m_Е · c ² )] ^0,5 | =

= 2 m_Е / [ m(p⁺) + m_Е ] = 729,71· 10 ^-5 - константа электромагнитных взаимодействий (постоянная тонкой структуры вещества – фундаментальная постоянная) [8, 9];

m(p⁺) = 273,1 m_Е = 273,1· 9,1091· 10 ^-31 = 2487,695 · 10 ^-31 [ кг ] -

- масса p⁺ мезона;

k_В = 386,143· 10 ^-15 - коэффициент пропорциональности;

R_Y = R_R · с = 1,097· 10 ⁷ · 2,99795· 10 ⁸ = 3,29 · 10 ¹⁵ [ 1 / с ] – постоянная Ридберга, выраженная в герцах.

Полученное значение является потенциалом ионизации атома водорода и показывает величину энергии связи электрона с атомом водорода.

Соотношение (8) и принцип относительности, согласно которому величина внутренней энергии тела с массой m = определяется выражением:

Е_Е = m · с ² (9)

где с = 3 ·10 ⁸ [ м / с ] – скорость света в вакууме.

Уменьшив внутреннюю энергию электрона на величину энергии связи электрона Е_С можем получить значение радиуса R_К керна электрона:

W = е²/2С = е²/2R_К = (m_Е · с ² - Е _С ) (10)

После преобразований в систему СИ получим:

R_К = е ² / [2( m_Е · с ² - Е_С ) · 1,1125·10^-10 ] =

= (1,6 ·10^-19)²/{2·[9,11·10^-31·(3 ·10⁸)² - 13,59·1,6 ·10^-19]·1,1125·10^-10 } =

= 1,4 ·10^-15 [м],

радиус которого практически равен радиусу свободного электрона.

Литература

1. Глинка Н.Л. Общая химия. М. – Ленинград. Химия. 1966. 688 с.

2. Френкель Я.И. Введение в теорию металлов. Ленинград, Наука, 1972. 424 с.

3. Эмсли Д. Элементы. М. Мир. 1993. 256 с.

4. Тамм И.Е. Основы теории электричества. М. Наука. 1976.

5. Поройков И.В. Краткий курс лекций по физике. М. Высшая школа . 1065. 495 с.

6. Грабовский Р.И. Курс физики. М. Высшая школа. 1980. 608 с.

7. Вихман Э. Берклеевский курс физики. Т. 4. Квантовая механика. М. Наука. 1977.

8. Гусев. В.П., Земсков А.А., Орлов П.С. Разработка новых моделей молекулярных связей и строения вещества на примере водорода.//Материалы докладов межвузовской научено-методической конференции. II ч. Ярославль. ЯГСХА. 1995. С. 219-222.

9. Гусев. В.П., Орлов П.С., Земсков А.А. Описания структур бериллия (новые модельные представления). //Физическая мысль России. № 1, 2003 г. М. МГУ. С. 101 – 104.

10. Китайгородский А.И. Введение в физику. М. Государственное издательство физико – математической литературы. 1959. 704 с.

11. Орлов П.С., Гусев. В.П. Определение теоретического предела прочности стали исходя из электронной теории строения вещества. // Актуальные пробемы инженерной науки в АПК. Международная научно – практическая конференция. Сборник научных трудов. Ч. III. Ярославль. ФГСХА. 2005.С. 90-99.

12. Краткий справочник физико – химических величин. Под ред. К.П. Мищенко, А.А. Равделя. Ленинград. Химия. 1967. 182 с.

mailto:mvtoroi@mail.ru